महत्वपूर्ण सूत्र: लोगारिदम (Logarithms) | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download
लॉगेरिदम
लॉगेरिदम एक गणितीय फ़ंक्शन है जिसका उद्देश्य यह निर्धारित करना है कि किसी विशेष आधार को एक निर्दिष्ट संख्या प्राप्त करने के लिए कितने उच्चतम पर बढ़ाना होगा। यह घातांक के विपरीत कार्य के रूप में खड़ा होता है।

लॉगेरिदम का सामान्य सूत्र
- b वह आधार है जिसका लॉगेरिदम है।
- y वह संख्या है जिसके लिए हम घातांक ज्ञात करना चाहते हैं।
- x वह घातांक है जिस पर b को बढ़ाना होगा ताकि y प्राप्त हो सके।
परिभाषा एवं लॉगरिदमिक सूत्र
लॉगेरिदम उस घातांक का प्रतिनिधित्व करते हैं जिस पर एक संख्या को दूसरे निर्दिष्ट संख्या को प्राप्त करने के लिए बढ़ाना आवश्यक है।
लॉगेरिदम के प्रकार
दो प्रकार के होते हैं:
- सामान्य लॉगेरिदम
- प्राकृतिक लॉगेरिदम
सामान्य लॉगेरिदम
10 के आधार वाला लॉगेरिदम सामान्य लॉगेरिदम के रूप में जाना जाता है और इसे log10 X के रूप में व्यक्त किया जाता है। यदि आधार निर्दिष्ट नहीं किया गया है, तो इसे 10 मान लिया जाता है।
(a) प्राकृतिक लॉगेरिदम: (b) 'e' के आधार वाला लॉगेरिदम प्राकृतिक लॉगेरिदम के रूप में जाना जाता है और इसे loge X के रूप में व्यक्त किया जाता है।
महत्वपूर्ण नोट: यदि आधार निर्दिष्ट नहीं किया गया है, तो हमेशा आधार को 10 मान लें।
लॉगेरिदम के लिए सूत्र
- loga X = 1
- loga 1 = 0
- loga (xp) = p(loga x)
- loga (xy) = loga X + loga Y
log(2 से 10 तक के मान: याद रखें
- Log 2 = 0.301
- Log 3 = 0.477 ≈ 0.48
- Log 4 = 0.60
- Log 5 = 0.698 ≈ 0.7
- Log 6 = 0.778 ≈ 0.78
- Log 7 = 0.845 ≈ 0.85
- Log 8 = 0.90
- Log 9 = 0.954 ≈ 0.96
- Log 10 = 1
लॉगेरिदम सूत्र (एंटी लॉग):
- एंटी लॉग एक लॉगेरिदम का विपरीत फ़ंक्शन है। logb x = y का अर्थ है कि एंटी लॉग (b) y = x।
- किसी भी समस्या को समझने का सबसे अच्छा तरीका है हल किए गए उदाहरण पर नज़र डालना। हम यहाँ ऐसा ही करने जा रहे हैं और हल किए गए उदाहरण से एंटी लॉग समस्या को समझेंगे।
उदाहरण
उदाहरण 1: यदि log 27= 1.431 है, तो log 9 का मान क्या है? (क) 0.945 (ख) 0.934 (ग) 0.958 (घ) 0.954
उत्तर: (घ) log 27= 1.431 ⇒ log(3)³= 1.431 ⇒ 3log 3= 1.431 ⇒ log3= 0.477
इसलिए, log9= log 3²= 2 log3= (2×0.477)= 0.954
उदाहरण 2: समीकरण को हल करें log x= 1- log(x-3) (क) 2 (ख) 1/2 (ग) 5 (घ) 4
उत्तर: (ग) दोनों समीकरणों को मिलाने पर हमें मिलता है logx log (x-3)=1 ⇒ log(x(x-3))= log 10¹
अब इसे गुणनात्मक रूप में बदलते हैं, x (x-3)= 10¹
x² – 3x-10= 0 ⇒ (x-5)(x+2)=0
x= -2, x=5
इस समीकरण को हल करने पर हमें x के लिए दो मान मिलते हैं: x= -2, x=5
x के विभिन्न मानों को अलग-अलग समीकरणों में डालकर हल करें:
- x= -2 ⇒ log(-2) = 1- log (-2-3)
- x= 5 ⇒ log5 = 1-log(5-3)
log5 = 1-log2
लॉगरिदम में नकारात्मक मान को नहीं माना जाता है। इसलिए, हमारे पास x का एकमात्र मान है, अर्थात् x=5।
उदाहरण 3: यदि log10 5 log(5x + 1) = log10 (x + 5) - 1, तो X का मान खोजें? (क) 3 (ख) 1 (ग) 10 (घ) 5
उत्तर: (क) log10 5 log(5x + 1) = log10 (x + 5) - log10 10
log10 [5 (5x + 1)] = log10 (10 (x + 5))
5 (5x + 1) = 10 (x + 5)
5x + 1 = 2x + 10
3x = 9 ⇒ x=3।
उदाहरण 4: यदि log(a) = log(b), तो (क) a-b=1 (ख) a=b (ग) a*b=1 (घ) a2-b2 = 1
उत्तर: (ग) तो, a*b=1।
उदाहरण 5: log9 (3log2 (1 - log3 (1 - 2log2 x)))= 1/2। x का मान खोजें। (क) 2 (ख) 1/2 (ग) 1 (घ) 4
उत्तर: (क) log2(1 - log3(1 - 2log2 x) = 1
1 - log3 (1 - 2log2 x)= 2
log3 (1 - 2log2 x)= 1
1 - 2log2 x = 3
2log2 x = 2 ⇒ log2 x = 1 ⇒ x= 2।
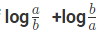
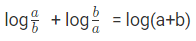
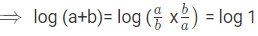
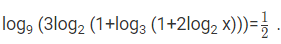
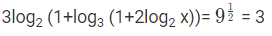
|
142 videos|172 docs|185 tests
|















