महत्वपूर्ण अवधारणाएँ और सूत्र: लोगारिदम (Logarithms) | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

लॉगरिदम क्या हैं?

लॉगरिदम को उस शक्ति के रूप में परिभाषित किया गया है, जिसके लिए एक संख्या को बढ़ाया जाना चाहिए ताकि कुछ अन्य मान प्राप्त किए जा सकें। यह बड़ी संख्याओं को व्यक्त करने का सबसे सुविधाजनक तरीका है। लॉगरिदम की विभिन्न महत्वपूर्ण विशेषताएँ हैं जो सिद्ध करती हैं कि लॉगरिदम के गुणन और भाग को जोड़ने और घटाने के लॉगरिदम के रूप में भी लिखा जा सकता है। “एक सकारात्मक वास्तविक संख्या a का लॉगरिदम, जो आधार b के संदर्भ में है, एक सकारात्मक वास्तविक संख्या है जो 1 के बराबर नहीं है, वह गुणांक है जिसके द्वारा b को बढ़ाना आवश्यक है ताकि a प्राप्त हो।” अर्थात्, b^y = a ⇔ log_ba = y जहाँ,

• “a” और “b” दो सकारात्मक वास्तविक संख्याएँ हैं
• y एक वास्तविक संख्या है
• “a” को तर्क कहा जाता है, जो लॉगरिदम के अंदर है
• “b” को आधार कहा जाता है, जो लॉगरिदम के नीचे है।

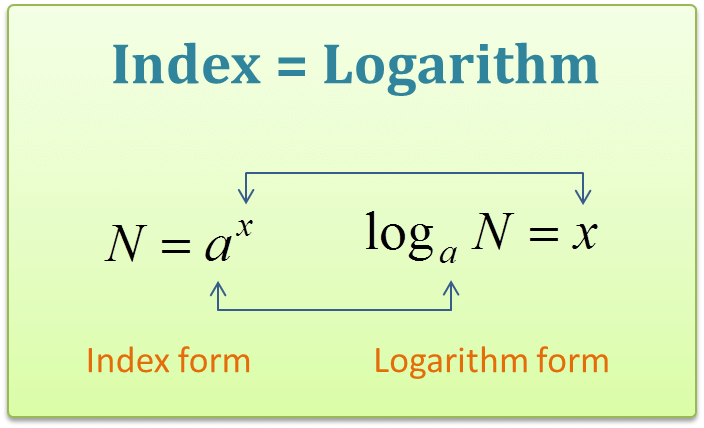
दूसरे शब्दों में, लॉगरिदम उस प्रश्न का उत्तर देता है “कितनी बार एक संख्या को गुणा किया जाता है ताकि दूसरी संख्या प्राप्त हो?” उदाहरण के लिए, 27 प्राप्त करने के लिए कितनी बार 3 को गुणा करना होगा? यदि हम 3 को 3 बार गुणा करते हैं, तो हमें उत्तर 27 मिलता है। इसलिए, लॉगरिदम 3 है। लॉगरिदम का रूप इस प्रकार लिखा जाता है: Log₃(27) = 3 ….(1) इसलिए, 27 का आधार 3 लॉगरिदम 3 है। उपरोक्त लॉगरिदम रूप को इस प्रकार भी लिखा जा सकता है: 3 x 3 x 3 = 27 या 3³ = 27 …..(2) इस प्रकार, समीकरण (1) और (2) दोनों समान अर्थ दर्शाते हैं। नीचे कुछ उदाहरण दिए गए हैं जो घातांक रूपों से लॉगरिदम में परिवर्तित करते हैं।

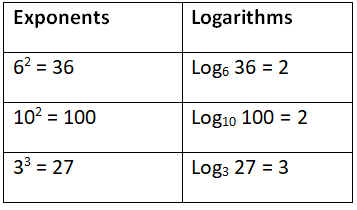
लॉगरिदम के प्रकार

(i) प्राकृतिक लॉगरिदम: loge N को प्राकृतिक लॉगरिदम या नैपेरियन लॉगरिदम कहा जाता है, जिसे (ln N) द्वारा दर्शाया जाता है, अर्थात्, जब लॉगरिदम का आधार “e” होता है, तब इसे प्राकृतिक लॉगरिदम कहा जाता है। उदाहरण: loge 7

(ii) सामान्य लॉगरिदम: log₁₀ N को ब्रिग्स लॉगरिदम कहा जाता है जब आधार 10 होता है। उदाहरण: log₁₀ 100

लॉगरिदम नियम

कुछ निश्चित नियम हैं जिनके आधार पर लॉगरिदमिक क्रियाएँ की जा सकती हैं। इन नियमों के नाम हैं:

• उत्पाद नियम
• भाग नियम
• घात नियम/घातांक नियम
• आधार परिवर्तन नियम
• आधार स्विच नियम
• लॉगरिदम का व्युत्पन्न
• लॉगरिदम का समाकल

आइए हम इन गुणों पर एक-एक करके नज़र डालते हैं।

1. उत्पाद नियम

इस नियम में, दो लॉगरिदमिक मानों का गुणा उनके व्यक्तिगत लॉगरिदम के योग के बराबर होता है। log_b (mn) = log_b m + log_b n
उदाहरण: log₃ (2y) = log₃ (2) + log₃ (y)

2. भाग नियम

दो लॉगरिदमिक मानों का भाग प्रत्येक लॉगरिदम के अंतर के बराबर होता है। log_b (m/n) = log_b m – log_b n
उदाहरण: log₃ (2/y) = log₃ (2) – log₃ (y)

3. घातांक नियम

घातांक नियम में, किसी संख्या m का लॉगरिदम यदि एक परिमेय घातांक n है, तो यह घातांक और उसके लॉगरिदम का गुणनफल के बराबर होता है। log_b (mⁿ) = n log_b m
उदाहरण: log_b(2³) = 3 log_b 2

4. आधार परिवर्तन नियम

log_b m = log_a m / log_a b
उदाहरण: log_b 2 = log_a 2 / log_a b

5. आधार स्विच नियम

log_b (a) = 1 / log_a (b)
उदाहरण: log_b 8 = 1 / log₈ b

6. लॉगरिदम का व्युत्पन्न

यदि f (x) = log_b (x), तो f(x) का व्युत्पन्न इस प्रकार दिया जाता है; f'(x) = 1 / (x ln(b))
उदाहरण: f (x) = log₁₀ (x) तब, f'(x) = 1 / (x ln(10))

7. लॉगरिदम का समाकल

∫log_b(x)dx = x(log_b(x) – 1/ln(b)) + C
उदाहरण: ∫ log₁₀(x) dx = x ∙ (log₁₀(x) – 1 / ln(10)) + C

लॉगरिदम गुण

• loga 1 = 0, a > 0, a ≠ 1
• loga a = 1, a > 0, a ≠ 1
• Log_a (ax) = x, x ∀ x ∈ R, x > 0
• a^{log_a x = x, x ∀ x ∈ R, x > 0}
• loga (m.n) = log_a m + log_a n, n ∀ m, n > 0, a > 0, a ≠ 1
• loga (m/n) = log_a m – log_a n, n ∀ m, n > 0, a > 0, a ≠ 1
• loga (mⁿ) = n log_a m, m ∀ m, m > 0, a > 0, a ≠ 1
• loga (1/m) = – log_a m, m ∀ m, n > 0, a > 0, a ≠ 1

जब 0 < a="" />< 1="" तब="" />loga b ≥ log_a c, ⇔ b ≤ c

जब a > 1 तब loga b ≥ log_a c, ⇔ b ≥ c > 0

विशेषताएँ और मैनटिस्सा

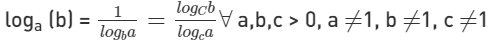
विशेषता: लॉगरिदम का संपूर्ण भाग जिसे विशेषता कहा जाता है। मैन्टिस्सा: दशमलव भाग जिसे मैन्टिस्सा कहा जाता है और यह हमेशा सकारात्मक होता है।

उदाहरण के लिए, log 3274 = 3.5150 में, संपूर्ण भाग 3 है, अर्थात् विशेषता 3 है और दशमलव भाग .5150 है, अर्थात् मैन्टिस्सा .5150 है।

विशेषताओं के बारे में याद रखने योग्य बिंदु:

• एकता (i.e., 1) से कम सकारात्मक संख्या के सामान्य लॉगरिदम की विशेषता नकारात्मक होती है।
• एकता (i.e., 1) से बड़ी सकारात्मक संख्या के सामान्य लॉगरिदम की विशेषता सकारात्मक होती है।
• यदि किसी आधार a के लिए लॉगरिदम विशेषता ‘n’ देता है, तो संभावित संपूर्ण मानों की संख्या an 1 − an द्वारा दी जाती है। उदाहरण के लिए, log10 x = n.abcd, तो x के लिए संभावित संपूर्ण मान 10n 1 − 10n द्वारा दी जाती है।
• यदि log10 x की विशेषता नकारात्मक (i.e., − n) है, तो दशमलव और दशमलव के बाद पहले महत्वपूर्ण संख्या के बीच के शून्यों की संख्या (n − 1) होती है।

महत्वपूर्ण रूपांतरण:

• यदि a > 1, a 1, c > 0 है, तो a b > c ⇔ loga c < />
• यदि 0 < a="" />< 1,="" a="" 1,="" c="" /> 0 है, तो a b > c ⇔ loga c > b।

महत्वपूर्ण सूत्र

• logb(mn) = logb(m) + logb(n)
• logb(m/n) = logb(m) – logb(n)
• Logb(xy) = y logb(x)
• Logbm√n = logb n/mm
• logb(x)n logb(y) = logb(xmyn)
• logb(mn) = logb(m) + logb(1/nm)
• logb(m – n) = logb(m) + logb(1-n/m)

हल किए गए उदाहरण

प्रश्न 1: यदि log2X log4X = log0.25√6 और x > 0, तो x है:

A. 6-1/6

B. 61/6

C. 3-1/3

D. 61/3

सही उत्तर विकल्प (A) है।

• log2x log4x = log0.25√6 हम समीकरण को इस प्रकार लिख सकते हैं: ⇒ log2x * 3 = 2log0.25√6
• ⇒ log2x3 = -log46 ⇒ ⇒ ⇒ 2log2x3 = -log26
• log26X6 = 0 log26X6 = 0
• 6x6 = 1 x6 = 1/6
• प्रश्न है "यदि log2X log4X = log0.25 √6 और x > 0, तो x है"

इसलिए, उत्तर है "6-1/6"।

प्रश्न 2: log9 (3log2 (1 log3 (1 2log2x))) = 1/2. x ज्ञात करें।

A. 4

B. 1/2

C. 1

D. 2

सही उत्तर विकल्प (D) है।

log9 (3log2 (1 log3 (1 2log2x))) = 1/2

3log2(1 log3(1 2log2x)) = 91/2 = 3 log2(1 log3(1 2log2x) = 1

1 log3(1 2log2x) = 2 log3(1 2log2x) = 1

1 2log2x = 3 2log2x = 2 log2x = 1 x = 2

प्रश्न है "x ज्ञात करें।"

इसलिए, उत्तर है "2"।

प्रश्न 3: यदि 22x 4 – 17 × 2x 1 = –4, तो निम्नलिखित में से कौन सा सत्य है?

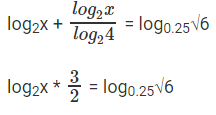
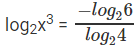
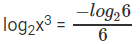
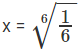
क. x एक सकारात्मक मान है

ख. x एक नकारात्मक मान है

ग. x एक सकारात्मक मान या नकारात्मक मान हो सकता है

घ. इनमें से कोई नहीं

सही उत्तर विकल्प (ग) है।

2x⁴ – 17 * 2x¹ = – 4 => 2x¹ = y

22x² = y²

22(22x²) – 17 * 2x¹ = –4

4y² – 17y + 4 = 0

4y² – 16y – y = 0

y = 0 या 4y (y – 4) – 1 (y – 4) = 0

y = 1/4 या 4

2x¹ = 1/4 या 4

⇒ x¹ = 2 या –2, x = 1 या –3

प्रश्न है "निम्नलिखित में से कौन सा सत्य है?"

इसलिए, उत्तर है "x एक सकारात्मक मान या नकारात्मक मान हो सकता है"।

प्रश्न 4: यदि log₁₂27 = a, log₉16 = b, तो log₈108 ज्ञात कीजिए।

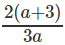
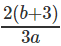
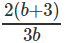
log₈108 = log₈(4 * 27) = log₈4 + log₈27

⇒ log₈4 = 2/3

log₈27 = 2 * log₁₆9, log₉16 = b, log₁₆ = 1/b

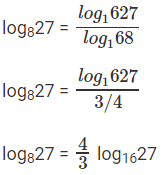
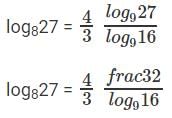
log₈27 = 2/b

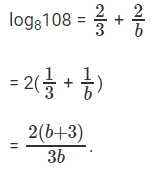
प्रश्न है "log₈108 ज्ञात कीजिए।"

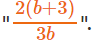
प्रश्न 5: यदि a, b पूर्णांक हैं, ऐसी स्थिति में x = a, और x = b इस असमानता को संतुष्ट करते हैं, तो a – b का अधिकतम संभव मान ज्ञात कीजिए।

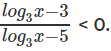
क. 214

ख. 216

ग. 200

घ. 203

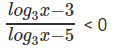
log₃x = y

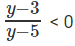
y ∈ (3, 5), 3 < />₃x < 5,="" 27="" />< x="" />< />

इसलिए अधिकतम (a – b) तब होगा जब a = 242 और b = 28। इसलिए, max(a – b) = 214।

प्रश्न है "a – b का अधिकतम संभव मान ज्ञात कीजिए।"

इसलिए, उत्तर है "214"।

प्रश्न 6: log₅x = a (इसका अर्थ है log x को आधार 5 पर a के बराबर पढ़ा जाए) log₂₀x = b। log_x10 क्या है?

क.

ख. (a b) * 2ab

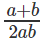
ग.

घ.

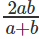
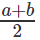
दिया गया, log₅x = a, log₂₀x = b, log_x5 = 1/a

log_x20 = 1/b ⇒

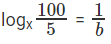
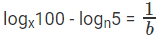
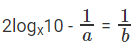
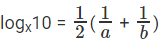
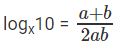
प्रश्न है "log_x10 क्या है?"

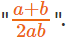
प्रश्न 7: log₃x log_x3 = 17/4। x ज्ञात कीजिए।

A. 34

B. 31/8

C. 31/4

D. 31/3

log₃x log_x3 = 17/4

मान लें कि y = log₃x। हमें पता है कि log_x3 =

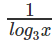
इसलिए log_x3 = 1/y

इस प्रकार समीकरण को इस तरह लिखा जा सकता है

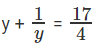
4y² - 17y + 4 = 0। उपर्युक्त समीकरण को हल करने पर हमें y = 4 या 1/4 मिलता है।

अगर y = 4 तो log₃x = 4 तब x = 3⁴। अगर y = 1/4 तो

log₃x = 1/4

तब x = 3^1/4। प्रश्न है "x का मान ज्ञात करें।"

इसलिए, उत्तर है "3⁴"।

प्रश्न 8: log_xy log_yx² = 3। log_xy³ ज्ञात करें।

A. 31/2

D. 31/16

सही उत्तर विकल्प (B) है।

log_xy log_yx² = 3 मान लें a = log_xy

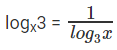
log_yx² = 2 log_yx। हमें पता है कि log_yx =

इसलिए उपरोक्त से log_yx = 1/a

अब समीकरण को फिर से लिखते हैं log_xy log_yx² = 3

a का उपयोग करके हमें मिलता है

अर्थात, a² - 3a = 0। हल करने पर हम पाते हैं a = 2 या 1। यदि a = 2, तो log_xy = 2 और log_yx³ = 3 log_xy = 6। या यदि a = 1, तो log_xy = 1 और log_yx³ = 3 log_xy = 3।

प्रश्न है "log_xy³ ज्ञात करें।"

इसलिए, उत्तर है "3"।

प्रश्न 9: log₂4 * log₄8 * log₈16 * ……………nth term = 49, n का मान क्या है?

A. 49

B. 48

C. 34

D. 24

पहले, L.H.S के nth term को पैटर्न देखकर परिभाषित करने की आवश्यकता है: यह log(2n) 2.2ⁿ है। दिया गया, log₂4 * log₄8 * log₈16 * ……………log(2n) 2.2ⁿ = 49। जब भी एक लॉगरिदम समीकरण को हल करते हैं, सामान्यतः किसी एक ही आधार को समान बनाने की दिशा में कार्य करना चाहिए। आधार को 2 बनाते हुए:-

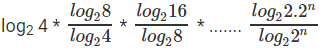
log(2n) 2.2ⁿ = 49, log(2n) 2 log(2n) 2ⁿ = 49, n = 49 n = 48

प्रश्न है "n का मान क्या है?"

इसलिए, उत्तर है "48"।

प्रश्न 10: यदि 3³ 6 9 ……… 3^x = x का मान क्या है?

C. 7

D. 11

सबसे पहले, हमें xवीं शर्त को परिभाषित करना होगा।

जब भी आप एक विशिष्ट संख्या का सामना करते हैं, जैसे कि ऊपर दिए गए समीकरण के R.H.S में, हमेशा उसके संदर्भ में महत्व को खोजने की कोशिश करें।

इस मामले में L.H.S में 3a है, इसलिए यह कुछ रूप में 3a होना चाहिए।

थोड़ी कोशिश और परीक्षण के साथ, आप पा सकते हैं

33(1 2 3 ...X) = 3 -3 * -66 ⇒ 33 * 3x(x 1)/2 = 33*66

x(x 1) = 132 इस समीकरण को x > 0 के लिए हल करते हुए, हमें x = 11 मिलता है। आपको सीधे यह देखना चाहिए कि 132 = 11 * 12 => x= 11 और पूरी समीकरण को हल करने में समय बर्बाद करने से बचें।

प्रश्न है "x का मान क्या है?"

इसलिए, उत्तर है "11"।

प्रश्न 11: x, y, z 3 पूर्णांक हैं जो एक जियोमेट्रिक अनुक्रम में हैं, ऐसा कि y - x एक पूर्ण घन है। दिया गया है, log36x2 log6√y log216y1/2z = 6। x, y, z का मान ज्ञात करें।

A. 189

B. 190

C. 199

D. 201

आइए समीकरण को सरल बनाने से शुरू करें:- ⇒ log62x2 log6y1/2 3log63y1/2z = 6

log6x log6y1/2y1/2z = 6 log6xyz = 6 xyz = 66

दिया गया x,y,z G.P. में हैं। मान लें x = a, y = ab, z = ab2 ⇒ xyz = a3b3 = (ab)3 (ab)3 = (62)3 समीकरण को संतुष्ट करने वाले (a,b) के संभावित मान:- (1, 36), (2, 18), (3, 12), (4, 9), (9, 4), (12, 3), (18, 2), (36, 1) दिया गया y-x एक पूर्ण घन है ⇒ ab-a एक पूर्ण घन है ⇒ a(b-1) एक पूर्ण घन है। केवल संभव जब (a, b) = (9, 4) ∴ x = 9, y = 36, z = 144 ∴ x y z = 9 36 144 = 189

प्रश्न है "x y z का मान ज्ञात करें।"

इसलिए, उत्तर है "189"।

प्रश्न 12: 10log(3 - 10logy) = log2(9 - 2y), y के लिए हल करें।

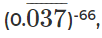
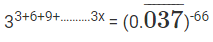
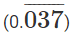
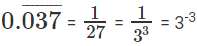
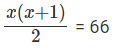
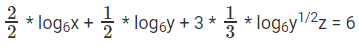
A. 0

C. 0 और 3

D. इनमें से कोई नहीं

समीकरण को सरल बनाने से पहले, यह मत भूलिए कि लॉग के अंदर कुछ भी नकारात्मक नहीं हो सकता है। 10log(3-y) = log2(9 - 2y) (y > 0)…………………………………(1) 3 - y = log2(9 - 2y) (अतः, 3 - y > 0 =) (y < 3))="" ………………………="" (2)="" />23-y = 9 - 2y 2y = t

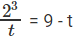
⇒ 8 = 9t – t² ⇒ t² - 9t + 8 = 0 ⇒ t² - t - 8t - 8 = 0 ⇒ t(t - 1) - 8(t - 1) = 0 ⇒ t = 1, 8। इसलिए, 2y = 1 और 2y = 8 ⇒ y = 0 और y = 3। हालाँकि, असमानताओं (1) और (2) के अनुसार, y इन मानों में से कोई भी नहीं ले सकता।

प्रश्न है "y के लिए हल करें।"

अतः, उत्तर है "इनमें से कोई नहीं"।

प्रश्न 13: 46 12 18 24 … 6x = (0.0625)-84, x का मान क्या है?

A. 7

C. 9

D. 12

दाईं ओर के व्यंजक को लें,

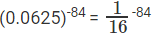
= (4-2)-84 = 4168। बाईं ओर के व्यंजक को लें 46 12 18 24 … 6x = 46(1 2 3 4 x) = 46 * 4(1 2 3 4 … x) = 46 * 4x(x + 1)/2 (x तक प्राकृतिक संख्याओं के योग का सूत्र का उपयोग करते हुए)। बाईं और दाईं ओर के व्यंजकों को बराबर करते हुए, हमें मिलता है 46 * 4x(x + 1)/2 = 4168 या 46 * 4x(x + 1)/2 = 46*28

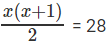
या x(x + 1) = 56। x के लिए हल करते हुए, हमें मिलता है, x = 7।

अतः, उत्तर है "7"।