Open App

RRB NTPC/ASM/CA/TA Exam > RRB NTPC/ASM/CA/TA Notes > Mathematics for RRB NTPC (Hindi) > टिप्स और ट्रिक्स: अंकगणितीय प्रगति

टिप्स और ट्रिक्स: अंकगणितीय प्रगति | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

अंकगणितीय प्रगति के उपाय

एक अंकगणितीय प्रगति (Arithmetic Progression) जिसमें प्रारंभिक पद 'a' और लगातार सदस्यों के बीच सामान्य अंतर 'd' है, की n-वीं पद को इस प्रकार व्यक्त किया जाता है: an = a + (n−1)d, जहाँ n = 1, 2, … है।

टिप्स और ट्रिक्स: अंकगणितीय प्रगति | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

अंकगणितीय प्रगति को हल करने के लिए सुझाव और उपाय

अंकगणितीय प्रगति को हल करने के लिए सुझाव और उपाय

अंकगणितीय प्रगति, जिसे अंकगणितीय अनुक्रम भी कहा जाता है, संख्याओं या पदों की एक श्रृंखला होती है जहाँ लगातार पदों के बीच का अंतर स्थिर रहता है। नीचे कुछ सरल सुझाव और उपाय दिए गए हैं जो आपको प्रतियोगी परीक्षाओं में अंकगणितीय प्रगति के प्रश्नों को शीघ्रता, आसानी और दक्षता से हल करने में मदद करेंगे।

अंकगणितीय प्रगति को इस रूप में प्रदर्शित किया जाता है: a, (a + d), (a + 2d), (a + 3d), … जहाँ a = पहला पद, और d = सामान्य अंतर है। n पदों की संख्या है। सामान्य रूप, Tn = a + (n-1)d जहाँ Tn एक अंकगणितीय प्रगति का n-वा पद है।

अंकगणितीय प्रगति के गुण

यदि एक निश्चित संख्या को AP के प्रत्येक पद में जोड़ा या घटाया जाता है, तो परिणामी श्रृंखला भी एक AP होगी और इसका सामान्य अंतर मूल AP के समान होगा।
यदि AP के प्रत्येक पद को एक निश्चित गैर-शून्य संख्या से विभाजित या गुणा किया जाता है, तो परिणामी श्रृंखला भी AP में होगी।
यदि n-वा पद रैखिक अभिव्यक्ति में है, तो श्रृंखला AP में है।
यदि a1, a2, a3, …, an और b1, b2, b3, …, bn AP में हैं, तो a1 b1, a2 b2, a3 b3, …, an bn और a1–b1, a2–b2, a3–b3, …, an–bn भी AP में होंगे।
यदि किसी श्रृंखला का n-वा पद Tn = An + B है, तो श्रृंखला AP में है।
तीन पदों को जिनका योग या गुणनफल दिया गया हो, a-d, a, a+d के रूप में मान लेना चाहिए।
चार पदों को जिनका योग या गुणनफल दिया गया हो, a-3d, a-d, a+d, a+3d के रूप में मान लेना चाहिए।

प्रकार 1: श्रृंखला का n-वा पद खोजें tn = a + (n − 1)d

उदाहरण 1: श्रृंखला 1, 3, 5, 7, … में 10वां पद खोजें: (a) 20 (b) 19 (c) 15 (d) 21 उत्तर: (b) tn = a + (n – 1)d जहाँ tn = n-वा पद, a = पहला पद, d = सामान्य अंतर, n = श्रृंखला में पदों की संख्या। दिए गए श्रृंखला में, a (पहला पद) = 1 और d (सामान्य अंतर) = 2 (3 – 1, 5 – 3)। इसलिए, 10वां पद = t10 = a + (n-1) d = 1 + (10 – 1) × 2 = 1 + 18 = 19।

उदाहरण 2: यदि श्रृंखला में 8 पद हैं, तो अंतिम पद खोजें: 13 , 17 , 21 , 25…. (a) 33 (b) 41 (c) 37 (d) 39 उत्तर: (b) हमें पता है कि, tn = a + (n – 1)d जहाँ tn = n-वा पद, a = पहला पद, d = सामान्य अंतर, n = श्रृंखला में पदों की संख्या। दिए गए श्रृंखला में, a (पहला पद) = 13 और d (सामान्य अंतर) = 4 (17 – 13, 21 – 17)। इसलिए, 8वां पद = t8 = a + (n-1) d = 13 + (8 – 1) × 4 = 13 + 28 = 41।

प्रकार 2: श्रृंखला में पदों की संख्या खोजें

उदाहरण 1: श्रृंखला 7, 11, 15, . . . 71 में पदों की संख्या खोजें: (a) 12 (b) 25 (c) 22 (d) 17 उत्तर: (d) हमें पता है कि, जहाँ n = पदों की संख्या, a = पहला पद, l = अंतिम पद, d = सामान्य अंतर। दिए गए श्रृंखला में, a (पहला पद) = 7, l (अंतिम पद) = 71, d (सामान्य अंतर) = 11 – 7 = 4। n = 16 + 1 = 17

उदाहरण 2: यदि पहला पद = 22, अंतिम पद = 50 और सामान्य अंतर 4 है, तो पदों की संख्या खोजें: (a) 10 (b) 9 (c) 8 (d) 7 उत्तर: (c) हमें पता है कि, जहाँ n = पदों की संख्या, a = पहला पद, l = अंतिम पद, d = सामान्य अंतर। दिए गए श्रृंखला में, a (पहला पद) = 22, l (अंतिम पद) = 50, d (सामान्य अंतर) = 4। n = 7 + 1 = 8

प्रकार 3: श्रृंखला के पहले 'n' पदों का योग खोजें

उदाहरण 1: श्रृंखला 1, 3, 5, 7…. 201 का योग खोजें: (a) 12101 (b) 25201 (c) 22101 (d) 10201 उत्तर: (d) हमें पता है कि, या जहाँ, a = पहला पद, d = सामान्य अंतर, l = tn = n-वा पद = a + (n-1)d। दिए गए श्रृंखला में, a = 1, d = 2, और l = 201। चूंकि हमें पता है कि, l = a + (n – 1) d 201 = 1 + (n – 1) × 2 201 = 1 + 2n -2 202 = 2n n = 101। Sn = 50.5 × (1 + 201) Sn = 50.5 × 202 Sn = 10201

उदाहरण 2: यदि इस श्रृंखला का पहला पद 45 है, सामान्य अंतर 5 है और इस श्रृंखला में पदों की संख्या 8 है, तो अंकगणितीय श्रृंखला का योग खोजें: (a) 500 (b) 300 (c) 400 (d) 200 उत्तर: (a) हमें पता है कि, या जहाँ, a = पहला पद, d = सामान्य अंतर, l = tn = n-वा पद = a + (n-1)d। दिए गए श्रृंखला में, a = 45, d = 5, और n = 8। Sn = 4 × (90 + 35) Sn = 4 × 125 Sn = 500

प्रकार 4: श्रृंखला का अंकगणितीय माध्य खोजें। b =

उदाहरण 1: पहले पाँच अभाज्य संख्याओं का अंकगणितीय माध्य खोजें: (a) 6.6 (b) 3.6 (c) 5.6 (d) 7.6 उत्तर: (c) हमें पता है कि यहाँ, पाँच अभाज्य संख्याएँ 2, 3, 5, 7 और 11 हैं। इसलिए, उनका अंकगणितीय माध्य (AM) = (2 + 3 + 5 + 7 + 11) / 5 = 28 / 5 = 5.6।

उदाहरण 2: यदि दो संख्याओं का अंकगणितीय माध्य 24 है और पहली संख्या 10 है, तो दूसरी संख्या खोजें: (a) 32 (b) 38 (c) 34 (d) 36 उत्तर: (b) हमें पता है कि b = 38

tn = a + (n – 1)d जहाँ tn = n-वा पद, a = पहला पद , d = सामान्य अंतर, n = श्रृंखला में पदों की संख्या। दिए गए श्रृंखला में, a (पहला पद) = 1 d (सामान्य अंतर) = 2 (3 – 1, 5 – 3)। इसलिए, 10वां पद = t10 = a + (n-1) d

t10 = 1 (10 – 1) 2 t10 = 1 18 t10 = 19

उदाहरण 2: यदि इस श्रृंखला में 8 तत्व हैं, तो श्रृंखला में अंतिम तत्व ज्ञात करें: 13, 17, 21, 25....

(a) 33
(b) 41
(c) 37
(d) 39

उत्तर: (b) हमें ज्ञात है कि, tn = a (n – 1)d जहां tn = nवां तत्व, a = पहला तत्व, d = सामान्य अंतर, n = अनुक्रम में तत्वों की संख्या।

दी गई श्रृंखला में, a (पहला तत्व) = 13, d (सामान्य अंतर) = 4 (17 – 13, 21 – 17)

अतः, 8वां तत्व = t8 = a (n-1)d t8 = 13 (8 – 1) 4 t8 = 13 28 t8 = 41

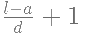
उदाहरण 1: श्रृंखला 7, 11, 15, ... 71 में तत्वों की संख्या ज्ञात करें।

(a) 12
(b) 25
(c) 22
(d) 17

उत्तर: (d) हमें ज्ञात है कि, जहां n = तत्वों की संख्या, a = पहला तत्व, l = अंतिम तत्व, d = सामान्य अंतर।

दी गई श्रृंखला में, a (पहला तत्व) = 7, l (अंतिम तत्व) = 71, d (सामान्य अंतर) = 11 – 7 = 4

n = 16 1 n = 17

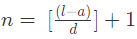
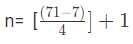
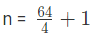
उदाहरण 2: यदि पहला तत्व = 22, अंतिम तत्व = 50 और सामान्य अंतर 4 है, तो तत्वों की संख्या ज्ञात करें।

(a) 10
(b) 9
(c) 8
(d) 7

उत्तर: (c) हमें ज्ञात है कि, जहां n = तत्वों की संख्या, a = पहला तत्व, l = अंतिम तत्व, d = सामान्य अंतर।

दी गई श्रृंखला में, a (पहला तत्व) = 22, l (अंतिम तत्व) = 50, d (सामान्य अंतर) = 4

n = 7 1 n = 8

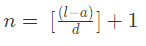
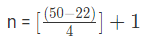
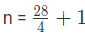
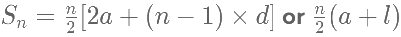
उदाहरण 1: श्रृंखला 1, 3, 5, 7…. 201 का योग ज्ञात करें।

(a) 12101
(b) 25201
(c) 22101
(d) 10201

उत्तर: (d) हमें ज्ञात है कि, या जहां, a = पहला तत्व, d = सामान्य अंतर, l = tn = nवां तत्व = a (n-1)d

दी गई श्रृंखला में, a = 1, d = 2, और l = 201

चूंकि हमें ज्ञात है कि, l = a (n – 1) d

201 = 1 (n – 1) 2

201 = 1 2n - 2

202 = 2n

n = 101

S_n = 50.5 (1 + 201)

S_n = 50.5 x 202

S_n = 10201

उदाहरण 1: पहले पांच अभाज्य संख्याओं का अंकगणितीय माध्य ज्ञात करें। (क) 6.6 (ख) 3.6 (ग) 5.6 (घ) 7.6 उत्तर: (ग) हम जानते हैं कि यहाँ, पांच अभाज्य संख्याएँ 2, 3, 5, 7 और 11 हैं। इसलिए, उनका अंकगणितीय माध्य (AM) :

उदाहरण 2: यदि दो संख्याओं का अंकगणितीय माध्य 24 है और पहली संख्या 10 है, तो दूसरी संख्या ज्ञात करें। (क) 32 (ख) 38 (ग) 34 (घ) 36 उत्तर: (ख) हम जानते हैं कि दूसरी संख्या को b मानते हैं। इसलिए, उनका अंकगणितीय माध्य (AM) :

उदाहरण 3: इस श्रृंखला का योग ज्ञात करें यदि इस श्रृंखला का पहला पद 45 है, सामान्य अंतर 5 है और इस श्रृंखला में पदों की संख्या 8 है। (क) 500 (ख) 300 (ग) 400 (घ) 200 उत्तर: (क) हम जानते हैं कि, या जहाँ, a = पहला पद, d = सामान्य अंतर, l = tn = nth पद = a (n-1)d। दिए गए श्रृंखला में, a = 45, d = 5, और n = 8। Sn = 4 (90 + 35) Sn = 4 x 125 Sn = 500

The document टिप्स और ट्रिक्स: अंकगणितीय प्रगति | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA is a part of the RRB NTPC/ASM/CA/TA Course Mathematics for RRB NTPC (Hindi).

All you need of RRB NTPC/ASM/CA/TA at this link: RRB NTPC/ASM/CA/TA

	Mathematics for RRB NTPC (Hindi) 142 videos\|172 docs\|185 tests

Mathematics for RRB NTPC (Hindi)

142 videos|172 docs|185 tests

Join Course for Free

About this Document

Oct 18, 2025 Last updated

Related Exams

RRB NTPC/ASM/CA/TA Bank Exams SSC JE SSC CGL

Document Description: टिप्स और ट्रिक्स: अंकगणितीय प्रगति for RRB NTPC/ASM/CA/TA 2025 is part of Mathematics for RRB NTPC (Hindi) preparation. The notes and questions for टिप्स और ट्रिक्स: अंकगणितीय प्रगति have been prepared according to the RRB NTPC/ASM/CA/TA exam syllabus. Information about टिप्स और ट्रिक्स: अंकगणितीय प्रगति covers topics like अंकगणितीय प्रगति को हल करने के लिए सुझाव और उपाय and टिप्स और ट्रिक्स: अंकगणितीय प्रगति Example, for RRB NTPC/ASM/CA/TA 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for टिप्स और ट्रिक्स: अंकगणितीय प्रगति.

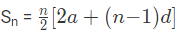
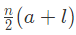
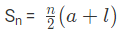
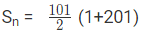
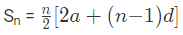
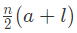
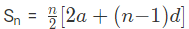
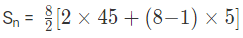
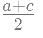
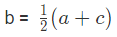
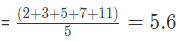
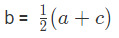
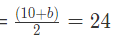
Introduction of टिप्स और ट्रिक्स: अंकगणितीय प्रगति in English is available as part of our Mathematics for RRB NTPC (Hindi) for RRB NTPC/ASM/CA/TA & टिप्स और ट्रिक्स: अंकगणितीय प्रगति in Hindi for Mathematics for RRB NTPC (Hindi) course. Download more important topics related with notes, lectures and mock test series for RRB NTPC/ASM/CA/TA Exam by signing up for free. RRB NTPC/ASM/CA/TA: टिप्स और ट्रिक्स: अंकगणितीय प्रगति | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

Description

Full syllabus notes, lecture & questions for टिप्स और ट्रिक्स: अंकगणितीय प्रगति | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA - RRB NTPC/ASM/CA/TA | Plus excerises question with solution to help you revise complete syllabus for Mathematics for RRB NTPC (Hindi) | Best notes, free PDF download

Information about टिप्स और ट्रिक्स: अंकगणितीय प्रगति

In this doc you can find the meaning of टिप्स और ट्रिक्स: अंकगणितीय प्रगति defined & explained in the simplest way possible. Besides explaining types of टिप्स और ट्रिक्स: अंकगणितीय प्रगति theory, EduRev gives you an ample number of questions to practice टिप्स और ट्रिक्स: अंकगणितीय प्रगति tests, examples and also practice RRB NTPC/ASM/CA/TA tests

	Mathematics for RRB NTPC (Hindi) 142 videos\|172 docs\|185 tests

Mathematics for RRB NTPC (Hindi)

142 videos|172 docs|185 tests

Join Course for Free

Download as PDF

Explore Courses for RRB NTPC/ASM/CA/TA exam

video lectures

study material

pdf

past year papers

ppt

Objective type Questions

Summary

Extra Questions

Free

Viva Questions

टिप्स और ट्रिक्स: अंकगणितीय प्रगति | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

Exam

MCQs

टिप्स और ट्रिक्स: अंकगणितीय प्रगति | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

Semester Notes

mock tests for examination

Important questions

practice quizzes

Previous Year Questions with Solutions

shortcuts and tricks

Sample Paper

;

Additional Information about टिप्स और ट्रिक्स: अंकगणितीय प्रगति for RRB NTPC/ASM/CA/TA Preparation

टिप्स और ट्रिक्स: अंकगणितीय प्रगति Free PDF Download

The टिप्स और ट्रिक्स: अंकगणितीय प्रगति is an invaluable resource that delves deep into the core of the RRB NTPC/ASM/CA/TA exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the टिप्स और ट्रिक्स: अंकगणितीय प्रगति now and kickstart your journey towards success in the RRB NTPC/ASM/CA/TA exam.

Importance of टिप्स और ट्रिक्स: अंकगणितीय प्रगति

The importance of टिप्स और ट्रिक्स: अंकगणितीय प्रगति cannot be overstated, especially for RRB NTPC/ASM/CA/TA aspirants. This document holds the key to success in the RRB NTPC/ASM/CA/TA exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

टिप्स और ट्रिक्स: अंकगणितीय प्रगति Notes

टिप्स और ट्रिक्स: अंकगणितीय प्रगति Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to टिप्स और ट्रिक्स: अंकगणितीय प्रगति. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, टिप्स और ट्रिक्स: अंकगणितीय प्रगति Notes on EduRev are your ultimate resource for success.

टिप्स और ट्रिक्स: अंकगणितीय प्रगति RRB NTPC/ASM/CA/TA Questions

The "टिप्स और ट्रिक्स: अंकगणितीय प्रगति RRB NTPC/ASM/CA/TA Questions" guide is a valuable resource for all aspiring students preparing for the RRB NTPC/ASM/CA/TA exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study टिप्स और ट्रिक्स: अंकगणितीय प्रगति on the App

Students of RRB NTPC/ASM/CA/TA can study टिप्स और ट्रिक्स: अंकगणितीय प्रगति alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the टिप्स और ट्रिक्स: अंकगणितीय प्रगति, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of टिप्स और ट्रिक्स: अंकगणितीय प्रगति is prepared as per the latest RRB NTPC/ASM/CA/TA syllabus.

Education Revolution