महत्वपूर्ण सूत्र: अंकगणितीय प्रगति (Arithmetic Progressions) | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download
अंकगणितीय प्रगति (AP)
अंकगणितीय प्रगति, जिसे अंकगणितीय अनुक्रम भी कहा जाता है, संख्याओं का एक अनुक्रम है जिसमें किसी भी दो लगातार सदस्यों के बीच का अंतर समान रहता है।
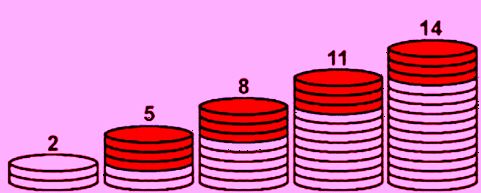
अंकगणितीय प्रगति का मूल सिद्धांत
प्रथम पद को a द्वारा दर्शाया जाता है। सामान्य अंतर को d द्वारा दर्शाया जाता है। nवां पद को an या tn द्वारा दर्शाया जाता है। पहले n पदों का योग Sn द्वारा दर्शाया जाता है। उदाहरण: 4, 8, 12, 16……..
अंकगणितीय प्रगति का सूत्र
AP का nवां पद ज्ञात करने का सूत्र है: Tn = a (n – 1) d, जहाँ tn = nवां पद, a = प्रथम पद, d = सामान्य अंतर, n = अनुक्रम में पदों की संख्या।
एक AP में पदों की संख्या
एक AP में पदों की संख्या ज्ञात करने का सूत्र है: n = ((l - a) / d) + 1, जहाँ n = पदों की संख्या, a = प्रथम पद, l = अंतिम पद, d = सामान्य अंतर।
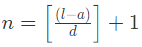
एक AP में पहले n पदों का योग
पहले n पदों का योग ज्ञात करने का सूत्र है: Sn = n/2 * (2a + (n - 1)d) या Sn = n/2 * (a + l), जहाँ a = प्रथम पद, d = सामान्य अंतर, tn = nवां पद = a + (n-1)d।
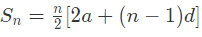
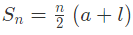
अंकगणितीय माध्य
यदि a, b, c AP में हैं, तो a और c का अंकगणितीय माध्य b है। अर्थात्, b = (a + c) / 2।
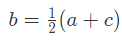
अंकगणितीय प्रगति के कुछ अन्य महत्वपूर्ण सूत्र
- पहले n प्राकृतिक संख्याओं का योग: पहले n प्राकृतिक संख्याओं का योग ज्ञात करने का सूत्र है: S = n(n + 1) / 2, जहाँ n = पहले n प्राकृतिक संख्याओं की संख्या।
- पहले n प्राकृतिक संख्याओं के वर्गों का योग: पहले n प्राकृतिक संख्याओं के वर्गों का योग ज्ञात करने का सूत्र है: S = n(n + 1)(2n + 1) / 6, जहाँ n = पहले n प्राकृतिक संख्याओं की संख्या।
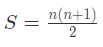
पहले n प्राकृतिक संख्याओं के वर्गों का योग ज्ञात करने का सूत्र है: S = पहले n प्राकृतिक संख्याओं के वर्गों का योग और n = पहले n प्राकृतिक संख्याओं की संख्या।
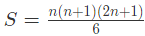
पहले n विषम संख्याओं का योग
- पहले n विषम संख्याओं का योग ज्ञात करने का सूत्र है: S = n2 जहाँ S = पहले n विषम संख्याओं का योग और n = पहले n विषम संख्याओं की संख्या।
पहले n सम संख्याओं का योग
- पहले n सम संख्याओं का योग ज्ञात करने का सूत्र है: S = n(n + 1) जहाँ S = पहले n सम संख्याओं का योग और n = पहले n सम संख्याओं की संख्या।
अंकगणितीय प्रगति के सूत्रों का उपयोग प्रश्नों में
Q1: एक अंकगणितीय प्रगति की पहले 20 अंशों का योग 610 है, और अगले 30 अंशों का योग 2130 है। इस अंकगणितीय प्रगति का सामान्य अंतर क्या है? (a) 8 (b) 10 (c) 12 (d) 15
उत्तर: (b) मान लीजिए कि अंकगणितीय प्रगति का पहला अंश ‘a’ है और सामान्य अंतर ‘d’ है। पहले 20 अंशों का योग इस प्रकार दिया गया है:
पहले 20 अंशों का योग: S1 = 20a + 190d = 610
अगले 30 अंशों का योग: S2 = 30a + 590d = 2130
इन समीकरणों को हल करते हुए, हमें मिलता है: d = 10। इसलिए, सही उत्तर (b) 10 है।
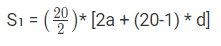
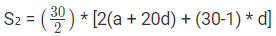
Q2: एक अंकगणितीय प्रगति के पहले 50 अंशों का योग 4800 है। यदि पहला अंश 12 है और सामान्य अंतर -3 है, तो 30वां अंश ज्ञात करें। (a) -14 (b) -17 (c) -20 (d) -75
उत्तर: (d) पहले 50 अंशों का योग इस प्रकार दिया गया है: S50 = 4800। अब, 30वां अंश ज्ञात करने के लिए, हम अंकगणितीय प्रगति के nth अंश का सूत्र उपयोग कर सकते हैं:
a30 = a + (n-1) * d
a30 = 12 + (30-1) * (-3)
a30 = 12 - 87
a30 = -75। सही उत्तर -75 है।
प्रश्न 3: एक अंकगणितीय प्रगति (Arithmetic Progression) की 10वीं पद 6वीं पद के तीन गुना के बराबर है। यदि पहले 10 पदों का योग 220 है, तो प्रगति का सामान्य अंतर (common difference) क्या है? (क) 6 (ख) 8 (ग) 10 (घ) 12 उत्तर: (ख) मान लें कि अंकगणितीय प्रगति का पहला पद ‘a’ है, और सामान्य अंतर ‘d’ है। समस्या के अनुसार, a + 9d = 3(a + 5d) इस समीकरण को हल करने पर हमें a = 10d मिलता है। अब, अंकगणितीय प्रगति के पहले 10 पदों का योग इस प्रकार दिया गया है: इस समीकरण को हल करने पर हमें d = 8 मिलता है। इसलिए, सही उत्तर (ख) 8 है।
प्रश्न 4: एक अंकगणितीय प्रगति में, 15वां पद 8वें पद से 8 अधिक है। यदि सामान्य अंतर 3 है, तो प्रगति का 10वां पद क्या है? (क) 21 (ख) 23 (ग) 25 (घ) 40 उत्तर: (घ) मान लें कि अंकगणितीय प्रगति का पहला पद ‘a’ है। तब, 8वां पद इस प्रकार दिया गया है: a + 7d = a + 21, और 15वां पद है a + 14d = a + 42। समस्या के अनुसार, a + 42 = (a + 21) + 8 इस समीकरण को हल करने पर हमें a = 13 मिलता है। अब, 10वां पद है a + 9d = 13 + 27 = 40। सही उत्तर 40 है।
प्रश्न 5: यदि अंकगणितीय प्रगति के पहले ‘n’ पदों का योग Sn = 5n² - 3n दिया गया है, तो प्रगति का पहला पद क्या है? (क) 2 (ख) 5 (ग) 7 (घ) 4 उत्तर: (घ) पहले ‘n’ पदों का योग इस प्रकार दिया गया है: इसे Sn = 5n² - 3n के साथ तुलना करने पर हमें 2a(n-1) * d = 5n - 3 मिलता है। चूंकि हम पहले पद ‘a’ की तलाश कर रहे हैं, हम ‘n’ को 1 मान सकते हैं: 2a(1-1) * d = 5 - 3 2a = 8 a = 4। सही उत्तर 4 है।
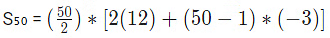
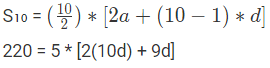
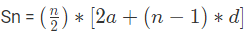
|
142 videos|172 docs|185 tests
|




















