विधियाँ और उपाय: ज्यामितीय प्रगति | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download
ज्यामितीय प्रगति के तरीके
एक ज्यामितीय प्रगति (GP) में, प्रत्येक अनुक्रमिक पद को उसके पूर्ववर्ती पद के साथ एक निश्चित संख्या को गुणा करके प्राप्त किया जाता है। यदि हम किसी उत्तरदायी पद को उसके पूर्ववर्ती पद से विभाजित करते हैं, तो हमें एक ऐसा मान प्राप्त होता है जो सामान्य अनुपात के बराबर होता है।

ज्यामितीय प्रगति के टिप्स, ट्रिक्स और शॉर्टकट्स
- तीन गैर-शून्य पद a, b, c तब और केवल तब GP में होते हैं जब b2 = ac।
- एक GP में, तीन अनुक्रमिक पदों को a/r, a, ar के रूप में लिया जा सकता है।
- यदि a, b और c तीन मात्राएँ GP में हैं, तो उनके व्युत्क्रम (b/a), (c/b), और (c/a) भी GP में होते हैं।
- यदि हम GP के प्रत्येक पद को एक गैर-शून्य मात्रा से गुणा या विभाजित करते हैं, तो परिणामी अनुक्रम उसी सामान्य अनुपात के साथ एक GP बना रहता है।
प्रकार 1: अनुक्रम के nवें पद को खोजें
उदाहरण 1: अनुक्रम 2, 4, 8, 16 में 11वाँ पद खोजें। (a) 2042 (b) 2200 (c) 1024 (d) 2048
उत्तर: (d) हम जानते हैं कि, an = arn-1 जहाँ r (सामान्य अनुपात) = 4/2 = 2, a1 = पहला पद = 2, an-1 = nवें पद से पूर्ववर्ती पद, n = पदों की संख्या। दिए गए अनुक्रम में, r (सामान्य अनुपात) = 4/2 = 2। इसलिए, 11वाँ पद = a11।
a11 = 2 × 211-1
a11 = 2 × 210
a11 = 2 × 1024
a11 = 2048
उदाहरण 2: यदि अनुक्रम में 7 पद हैं, तो अनुक्रम 3, 15, 75, 375 में अंतिम पद खोजें। (a) 46875 (b) 44875 (c) 42875 (d) 40875
उत्तर: (a) हम जानते हैं कि, an = arn-1 जहाँ r (सामान्य अनुपात) = 15/3 = 5, a1 = पहला पद = 3, an-1 = nवें पद से पूर्ववर्ती पद, n = पदों की संख्या। दिए गए अनुक्रम में, r (सामान्य अनुपात) = 15/3 = 5। इसलिए, 7वाँ पद = a7.
a7 = 3 × 57-1
a7 = 46875
प्रकार 2: अनुक्रम में पदों की संख्या खोजें
उदाहरण 1: अनुक्रम 2, 4, 8, 16 में 11वाँ पद खोजें। (a) 2042 (b) 2200 (c) 1024 (d) 2048
उत्तर: (d) हम जानते हैं कि, an = arn-1 जहाँ r (सामान्य अनुपात) = 4/2 = 2, a1 = पहला पद = 2, an-1 = nवें पद से पूर्ववर्ती पद, n = पदों की संख्या। दिए गए अनुक्रम में, r (सामान्य अनुपात) = 4/2 = 2। इसलिए, 11वाँ पद = a11.
a11 = 2 × 211-1
a11 = 2 × 210
a11 = 2 × 1024
a11 = 2048
उदाहरण 2: यदि इस श्रृंखला में 7 पद हैं 3, 15, 75, 375 … (क) 46875 (ख) 44875 (ग) 42875 (घ) 40875 उत्तर: (क) हमें पता है कि, an = arn-1 जहाँ r (सामान्य अनुपात) = 15/3 = 5 a1 = पहला पद = 3, an-1 = nth पद से पहले का पद, n = पदों की संख्या दिए गए श्रृंखला में, r (सामान्य अनुपात) = 15/3 = 5 इसलिए, 7वां पद = a7 a7 = 3 x 57-1 a7 = 46875
हमें पता है कि, दिए गए श्रृंखला में, a1 = 10, a2 = 40, r = 40/10 = 4 an = 10240 an = arn-1 10240 = 10 x 4n-1 (दोनों तरफ 10 से विभाजित करें) 1024 = 4n-1 45 = 4n-1 5 = n – 1 n = 6 इसलिए, श्रृंखला में 6 पद हैं।
प्रकार 3: ज्यामितीय श्रृंखला के पहले 'n' पदों का योग
- उदाहरण 1: श्रृंखला 1, 3, 9 …. का योग 121 के लिए कितने पद हैं (क) 18 (ख) 19 (ग) 13 (घ) 5 उत्तर: (घ) हमें पता है कि, दिए गए श्रृंखला में, a = 1, r = 3/1 = 3, Sn = 121 242 = (3n – 1) 243 = 3n 35 = 3n n = 5
- उदाहरण 2: दिए गए ज्यामितीय श्रृंखला का योग 9वें पद तक निकालें 7, 14, 28, 56…… (क) 3177 (ख) 3577 (ग) 1377 (घ) 5377 उत्तर: (ख) हमें पता है कि, दिए गए श्रृंखला में, a = 7, r = 14/7 = 2 = 3577
प्रकार 4: श्रृंखला का ज्यामितीय माध्य (GM) निकालें।
- उदाहरण 1: 2, 3, और 6 का ज्यामितीय माध्य क्या है? (क) 4.5 (ख) 6.5 (ग) 3.30 (घ) 6.4 उत्तर: (ग) हमें पता है कि, GM = (abc)1/3 इसलिए, ज्यामितीय माध्य (GM) = (2 x 3 x 6)1/3 = 3.30
- उदाहरण 2: 36 और 9 का ज्यामितीय माध्य क्या है? (क) 24 (ख) 16 (ग) 18 (घ) 14 उत्तर: (ग) हमें पता है कि, GM = (ab)1/2 इसलिए, ज्यामितीय माध्य (GM) = (36 x 9)1/2 = 18
उदाहरण 1: श्रृंखला 1, 3, 9 …. का योग 121 के लिए कितने पद हैं (क) 18 (ख) 19 (ग) 13 (घ) 5 उत्तर: (घ) हमें पता है कि, दिए गए श्रृंखला में, a = 1, r = 3/1 = 3, Sn = 121 242 = (3n – 1) 243 = 3n 35 = 3n n = 5
उदाहरण 2: दिए गए ज्यामितीय श्रृंखला का योग 9वें पद तक ढूंढें 7,14,28,56…… (क) 3177 (ख) 3577 (ग) 1377 (घ) 5377 उत्तर: (ख) हमें पता है कि, दिए गए श्रृंखला में, a = 7, r = 14/7 = 2 = 3577
प्रकार 4: श्रृंखला का ज्यामितीय माध्य (GM) ढूंढें।
उदाहरण 1: 2, 3, और 6 का ज्यामितीय माध्य क्या है? (क) 4.5 (ख) 6.5 (ग) 3.30 (घ) 6.4 उत्तर: (ग) हमें पता है कि, GM = (abc)1/3 इसलिए, ज्यामितीय माध्य (GM) = (2 x 3 x 6)1/3 = 3.30
उदाहरण 2: 36 और 9 का ज्यामितीय माध्य क्या है? (क) 24 (ख) 16 (ग) 18 (घ) 14 उत्तर: (ग) हमें पता है कि, GM = (ab)1/2 इसलिए, ज्यामितीय माध्य (GM) = (36 x 9)1/2 = 18

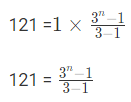

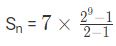
|
142 videos|172 docs|185 tests
|




















