महत्वपूर्ण सूत्र: ज्यामितीय प्रगति (Geometric Progressions) | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

ज्यामितीय प्रगति

ज्यामितीय प्रगति (Geometric Progression) एक संख्या अनुक्रम है जिसमें प्रत्येक पद, पहले के अलावा, एक निश्चित, शून्य से भिन्न संख्या से गुणा करके निर्धारित किया जाता है, जिसे सामान्य अनुपात (common ratio) कहा जाता है।

ज्यामितीय प्रगति के सूत्र

• सामान्य अनुपात: सामान्य अनुपात खोजने का सूत्र a2/a1
• ज्यामितीय प्रगति का nवां पद: nवां पद खोजने का सूत्र an = a1rn-1 जहां a1 = पहला पद, r = सामान्य अनुपात और n = पदों की संख्या
• ज्यामितीय प्रगति में पहले n पदों का योग: पहले n पदों के योग का मानक सूत्र
  • {यदि r>1} जहां, r = सामान्य अनुपात, a1 = पहला पद, n = पदों की संख्या
  • {यदि r<1} जहां,="" r="सामान्य" अनुपात,="" a1="पहला" पद,="" n="पदों" की="">
• अनंत ज्यामितीय प्रगति का योग: अनंत ज्यामितीय प्रगति के योग का सूत्र (यदि -1< />< />
• ज्यामितीय माध्य (GM): यदि दो शून्य से भिन्न संख्याएँ a और b ज्यामितीय प्रगति में हैं, तो उनका GM है GM = (ab)1/2। यदि तीन शून्य से भिन्न संख्याएँ a, b और c ज्यामितीय प्रगति में हैं, तो उनका GM है GM = (abc)1/3।

ज्यामितीय प्रगति के गुण

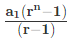
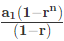
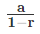
• यदि ‘a’ पहली संख्या है, r एक सीमित जी.पी. का सामान्य अनुपात है जिसमें m संख्याएँ हैं, तो अंत से nth संख्या होगी = a rm-n।
• अंतिम संख्या ‘l’ और सामान्य अनुपात r के साथ जी.पी. से अंत से nth संख्या है।
• जी.पी. में सभी संख्याओं का व्युत्क्रम भी जी.पी. के रूप में माना जाता है।
• जब सभी संख्याएँ जी.पी. को एक ही शक्ति में बढ़ाया जाता है, तो ज्यामितीय प्रगति की एक नई श्रृंखला बनती है।

ज्यामितीय प्रगति के सूत्रों का प्रश्नों में उपयोग

प्रश्न 1: यदि पहली संख्या (a) 3 है और सामान्य अनुपात (r) -2 है, तो ज्यामितीय प्रगति की 7वीं संख्या क्या होगी? (क) -192 (ख) 192 (ग) -96 (घ) 96 उत्तर: (ख) जी.पी. की nth संख्या दी गई है an = a * r(n-1)। मानों को प्रतिस्थापित करते हुए, a = 3, r = -2, और n = 7: a7 = 3 * (-2)(7-1) = 3 * (-2)6 = 3 * 64 = 192

प्रश्न 2: यदि अनंत ज्यामितीय प्रगति का योग 72 है और सामान्य अनुपात (r) 0.5 है, तो पहली संख्या (a) क्या होगी? (क) 2 (ख) 12 (ग) 24 (घ) 36 उत्तर: (घ) अनंत जी.पी. का योग S = a / (1 – r) द्वारा दिया गया है। मानों को प्रतिस्थापित करते हुए, S = 72 और r = 0.5: 72 = a / (1 – 0.5) 72 = a / 0.5 a = 72 * 0.5 a = 36

प्रश्न 3: यदि पहले 8 संख्याओं का योग (S8) 4374 है और पहली संख्या (a) 3 है, तो ज्यामितीय प्रगति का सामान्य अनुपात (r) क्या होगा? (क) 3 (ख) 2 (ग) 4 (घ) 5 उत्तर: (ख) पहले n संख्याओं का योग Sn = a * (rn – 1) / (r – 1) द्वारा दिया गया है। मानों को प्रतिस्थापित करते हुए, a = 3, S8 = 4374, और n = 8: 4374 = 3 * (r8 – 1) / (r – 1) अब, r के लिए हल करते हैं: 3 * (r8 – 1) = 4374 * (r – 1) r8 – 1 = 1458 * (r – 1) r8 – 1458r 1457 = 0 संख्यात्मक विधियों का उपयोग करते हुए, हम पाते हैं कि r ≈ 2.362

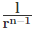
प्रश्न 4: यदि ज्यामितीय अनुक्रम का पहला पद (a) 2 है और सामान्य अनुपात (r) 3/4 है, तो पहले 5 पदों का योग क्या है? (a) 6.75 (b) 8.25 (c) 7.50 (d) 5.50 उत्तर: (c) एक ज्यामितीय अनुक्रम के पहले n पदों का योग निम्नलिखित सूत्र से दिया जाता है: S_n = a * (rⁿ – 1) / (r – 1)। मानों को प्रतिस्थापित करते हुए, a = 2, r = 3/4, और n = 5: S₅ = 2 * ((3/4)⁵ – 1) / (3/4 – 1) = 2 * (243/1024 – 1) / (-1/4) = 2 * (-781/1024) / (-1/4) = 7.50

प्रश्न 5: यदि ज्यामितीय अनुक्रम का चौथा पद 54 है और सामान्य अनुपात (r) 3 है, तो दसवां पद क्या है? (a) 1458 (b) 2187 (c) 729 (d) उपरोक्त में से कोई नहीं उत्तर: (d) एक ज्यामितीय अनुक्रम का nवां पद निम्नलिखित सूत्र से दिया जाता है: a_n = a * r^(n-1)। मानों को प्रतिस्थापित करते हुए, a = 54, r = 3, और n = 10: a₁₀ = 54 * 3^(10-1) = 54 * 3⁹ = 54 * 19683 = 1058841