हल किए गए उदाहरण: हार्मोनिक प्रगति | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download
एचपी की परिभाषा
एक हार्मोनिक प्रगति वास्तविक संख्याओं का एक प्रकार का अनुक्रम है जो अंकगणितीय प्रगति के व्युत्क्रम को प्राप्त करने के बाद बनाया जाता है।
हार्मोनिक प्रगति का सामान्य रूप
- इसे वास्तविक संख्याओं के एक सेट के रूप में वर्गीकृत किया जा सकता है, जहाँ अनुक्रम में प्रत्येक पद अपने दो निकटतम संख्याओं का हार्मोनिक माध्य दर्शाता है।
- इसके अतिरिक्त, जब अनुक्रम का उल्टा अंकगणितीय प्रगति के सिद्धांतों का पालन करता है, तो इसे हार्मोनिक प्रगति कहा जाता है। इसका मूल रूप से अर्थ है कि यदि a, a + d, a + 2d, आदि एक A.P. है, तो
मुख्य बिंदु
- एक हार्मोनिक प्रगति में पद अनिवार्य रूप से सकारात्मक और शून्य से अलग होते हैं। यह आवश्यकता उन पदों के व्युत्क्रम को परिभाषित करने की आवश्यकता से उत्पन्न होती है, क्योंकि शून्य द्वारा विभाजन अपरिभाषित रहता है।
- अंकगणितीय और ज्यामितीय प्रगति के विपरीत, हार्मोनिक प्रगति में कोई सीमित योग नहीं होता। हार्मोनिक प्रगति में पदों का कुल योग फैलता है, जो दर्शाता है कि जैसे-जैसे अधिक पद जोड़े जाते हैं, यह अनंत की ओर बढ़ता है।
हल किए गए उदाहरण
उदाहरण 1: हार्मोनिक प्रगति का अधिकतम आंशिक योग ज्ञात करें, यदि दूसरे और तीसरे पद क्रमशः 1/13 और 1/10 हैं। (क) 1.23 (ख) 1.63 (ग) 1.25 (घ) 1.09 उत्तर: (ख) हार्मोनिक प्रगति के पद हैं। इसलिए अधिकतम आंशिक योग है।
उदाहरण 2: 2 संख्याओं U, V के लिए, उनके बीच का हार्मोनिक माध्य क्या होगा? (क) (2v 2u )/3v (ख) 2uv/(u v) (ग) (u v)/2uv (घ) 2v/(u v) उत्तर: (ख) मान लीजिए w हार्मोनिक माध्य है, 2/w = 1/u + 1/v,


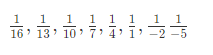
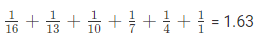
उदाहरण 3: यदि p, q, r हर्मोनिक प्रगति (h.p) में हैं, तो q, p और r से इस प्रकार जुड़ा है:
- (a) 2(1⁄q) = (1⁄p + 1⁄r)
- (b) 2(1⁄r) = (1⁄q + 1⁄r)
- (c) 2(1⁄p) = (1⁄p + 1⁄q)
- (d) उपरोक्त में से कोई नहीं
उदाहरण 4: H.P. 1/4, 1/8, 1/12, 1/16,… का 11वां पद ज्ञात करें।
- (a) 39/7
- (b) 1/44
- (c) 25/6
- (d) 25/7
उदाहरण 5: दो संख्याओं का A.M और G.M क्रमशः 27 और 26 है, तो H.M क्या होगा?
- (a) 22.54
- (b) 23.54
- (c) 25.03
- (d) 21.77
उदाहरण 6: दो संख्याओं 18 और 37 का हर्मोनिक माध्य का प्रतिवर्ती ज्ञात करें?
- (a) 1/15.31
- (b) 1/17.43
- (c) 1/24.21
- (d) 1/20.21
उदाहरण 7: दो संख्याओं 19 और 57 का हर्मोनिक माध्य ज्ञात करें?
- (a) 25.31
- (b) 27.34
- (c) 28.50
- (d) 24.21
उदाहरण 8: यदि दो सेट हैं जिनका हर्मोनिक माध्य 150 और 132 है और जिनमें 25 और 12 अवलोकन हैं, तो संयुक्त हर्मोनिक माध्य क्या होगा?
- (a) 7.85
- (b) 9.53
- (c) 5.82
- (d) उपरोक्त में से कोई नहीं
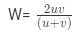
उदाहरण 9: 17, 22, 13, 26 का हार्मोनिक माध्य क्या होगा? (क) 14.32 (ख) 16.76 (ग) 17.90 (घ) 21.05 उत्तर: (घ) संख्या 17, 22, 13, 26 के लिए हार्मोनिक माध्य है -
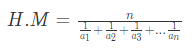
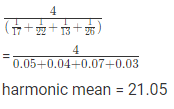
उदाहरण 10: 2 संख्याओं का हार्मोनिक माध्य खोजें जिनका ज्यामितीय माध्य (G.M.) और गणितीय माध्य (A.M.) क्रमशः 90 और 75 है? (क) 103 (ख) 116 (ग) 108 (घ) 117 उत्तर: (ग) G.M.² = A.M. × H.M.
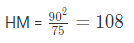
|
142 videos|172 docs|185 tests
|















