Open App

RRB NTPC/ASM/CA/TA Exam > RRB NTPC/ASM/CA/TA Notes > Mathematics for RRB NTPC (Hindi) > बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ)

बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

बार चार्ट क्या हैं?

बार चार्ट डेटा प्रस्तुत करने के लिए सबसे सरल, ग्राफिक रूप से आकर्षक और इसलिए सबसे आम तरीकों में से एक हैं। ये विशेष रूप से विभिन्न डेटा श्रृंखलाओं का प्रतिनिधित्व करने के लिए उपयोगी होते हैं।

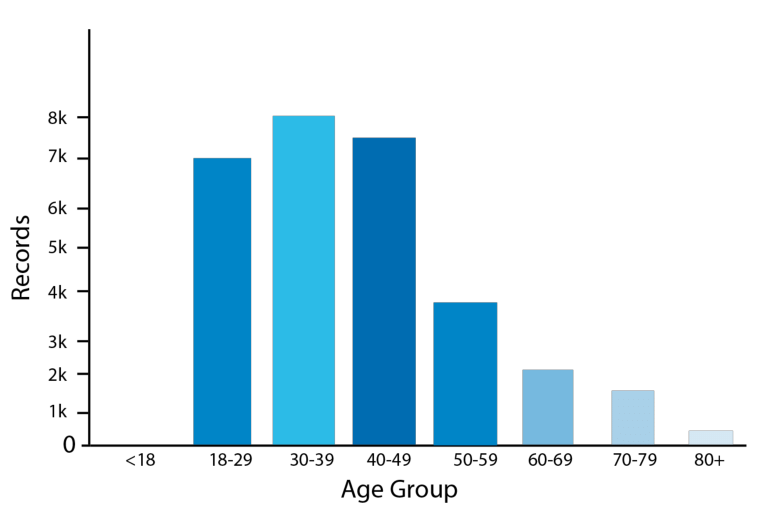
बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

डेटा श्रृंखला निरंतर चर को शामिल करती है, जबकि विशिष्ट उदाहरणों के मान, जिन पर डेटा श्रृंखला का मान मापा जाता है, विवेचनात्मक चर के मान का प्रतिनिधित्व करते हैं।
डेटा को बार चार्ट के रूप में प्रस्तुत करने से डेटा का तुलनात्मक अध्ययन बहुत आसान हो जाता है।
एक बार चार्ट में एक समूह होता है जो बार के एक समान दूरी पर होता है।
बार चार्ट पर मानों को बार की लंबाई या ऊंचाई के माप से पढ़ा जाता है।
बार की चौड़ाई अधिकांशतः अप्रासंगिक होती है और केवल प्रस्तुति की स्पष्टता के लिए उपयोग की जाती है।

अब हम विभिन्न प्रकार के बार चार्ट और उन डेटा के प्रकारों पर एक नज़र डालते हैं जिन्हें बार चार्ट पर प्रस्तुत किया जा सकता है।

1. सरल बार चार्ट

सरल बार चार्ट में एक निरंतर चर को एक विवेचनात्मक चर के साथ चार्ट किया जाता है।

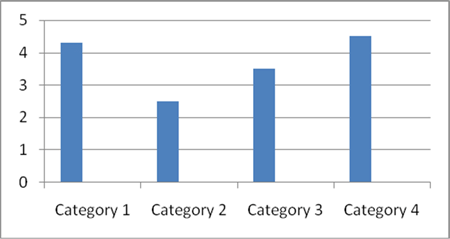
2. स्टैक्ड बार ग्राफ

इनका उपयोग विभिन्न श्रेणियों का निर्माण करने वाले उप-समूहों के बारे में जानकारी प्रदर्शित करने के लिए किया जाता है।

एक स्टैक्ड बार चार्ट में उप-समूहों का प्रतिनिधित्व करने वाले बार एक दूसरे के ऊपर रखे जाते हैं ताकि एकल कॉलम बनाया जा सके या एक ही बार बनाने के लिए एक साथ रखे जाते हैं।
बार की कुल ऊंचाई या लंबाई श्रेणी का कुल आकार दिखाती है, जबकि विभिन्न रंग या छायाएँ उप-समूह के सापेक्ष योगदान को इंगित करने के लिए उपयोग की जाती हैं।

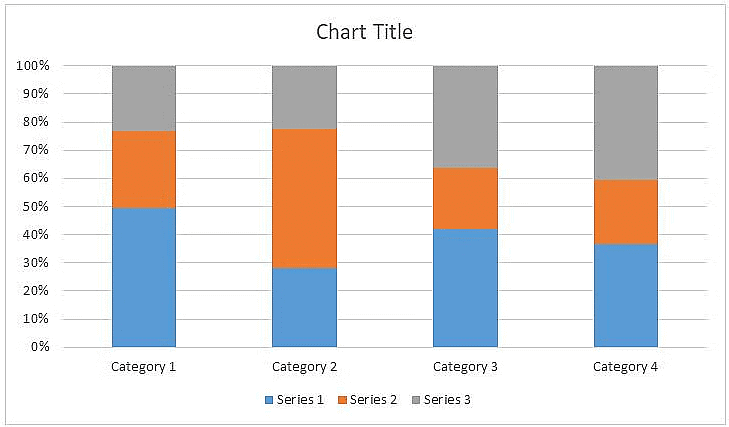
स्टैक्ड बार चार्ट का उपयोग यह दिखाने के लिए भी किया जाता है कि विभिन्न उप-समूह प्रत्येक अलग श्रेणी में कितना प्रतिशत योगदान करते हैं। इस मामले में, व्यक्तिगत श्रेणियों का प्रतिनिधित्व करने वाले बार सभी समान होते हैं।

3. समग्र बार चार्ट

सरल बार चार्ट की एक प्रमुख सीमा यह है कि इसका उपयोग केवल एक ही निरंतर चर को प्रदर्शित करने के लिए किया जा सकता है।

यदि एक ही बार चार्ट पर दो या दो से अधिक निरंतर चरों के सेट को दिखाना है, तो हम इसे संयोजित बार चार्ट कहते हैं। नीचे चित्र में संयोजित बार चार्ट का एक उदाहरण दिखाया गया है।

डिविएशन को दिखाने के लिए बार चार्ट का उपयोग

डिविएशन बार निरंतर चरों की ग्राफिक प्रस्तुति के लिए उपयोगी होते हैं जिनमें सकारात्मक और नकारात्मक दोनों मान हो सकते हैं, जैसे कि अधिशेष या घाटा, शुद्ध लाभ या हानि, आयात और निर्यात का शुद्ध।

सामान्यतः, निरंतर चरों को जिनमें सकारात्मक और नकारात्मक दोनों मान होते हैं, बार चार्ट पर सबसे अच्छे तरीके से प्रदर्शित किया जाता है।

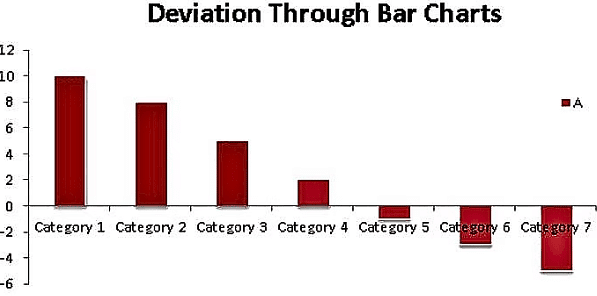
एक बेसलाइन बनाई जाती है और सकारात्मक मान (जैसे कि लाभ, अधिशेष, आदि) को बेसलाइन के ऊपर बार द्वारा प्रदर्शित किया जाता है, जबकि नकारात्मक डिविएशन (हानि या घाटा) को बेसलाइन के नीचे बार द्वारा प्रदर्शित किया जाता है, जैसा कि ऊपर के चित्र में दिखाया गया है।

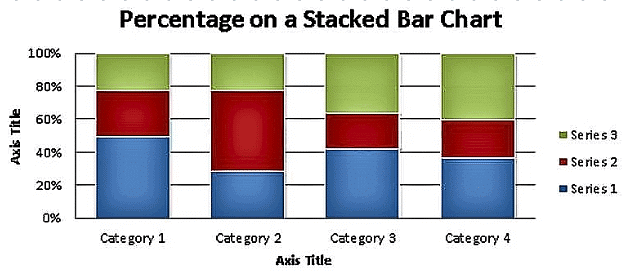
प्रतिशत का प्रतिनिधित्व स्टैक्ड बार चार्ट पर

कभी-कभी स्टैक्ड बार का उपयोग किसी निरंतर चर के टूटने का प्रतिनिधित्व करने के लिए भी किया जा सकता है। नीचे का चित्र इसे स्पष्ट करेगा।

इस प्रकार के बार चार्ट का उपयोग दो या दो से अधिक डेटा सेट की तुलना के लिए काफी सुविधाजनक है। नीचे का चित्र भारत सरकार के विभिन्न राजस्व स्रोतों का दो साल की अवधि में टूटना दिखाता है।

हल किए गए उदाहरण

प्रश्न 1: तीन कंपनियों X, Y और Z द्वारा वर्षों में कागज का उत्पादन (लाख टन में)। ग्राफ का अध्ययन करें और निम्नलिखित प्रश्नों का उत्तर दें।

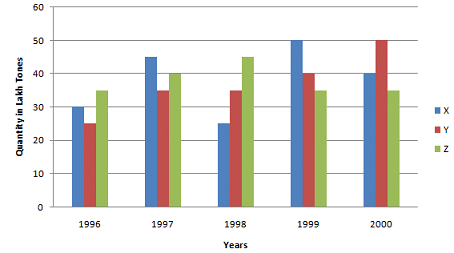
(i) कंपनी Z का 1998 में उत्पादन और कंपनी Y का 1996 में उत्पादन के बीच का अंतर क्या है? उत्तर: आवश्यक अंतर = [(45 - 25) * 1,00,000] टन = 20,00,000 टन।

(ii) 1998-2000 की अवधि में कंपनी X का औसत उत्पादन और उसी अवधि में कंपनी Y का औसत उत्पादन का अनुपात क्या है? उत्तर: 1998-2000 की अवधि में कंपनी X का औसत उत्पादन = [1/3 * (25 + 50 + 40)] = (115/3) लाख टन। 1998-2000 की अवधि में कंपनी Y का औसत उत्पादन = [1/3 * (35 + 40 + 50)] = (125/3) लाख टन। आवश्यक अनुपात = (115/3)/(125/3) = 115/125 = 23/25।

(iii) 1996 से 1999 तक कंपनी Y के उत्पादन में प्रतिशत वृद्धि क्या है? उत्तर: 1996 से 1999 तक कंपनी Y के उत्पादन में प्रतिशत वृद्धि = [(40 - 25)/25 * 100]% = (15/25 * 100)% = 60%।

(iv) पांच वर्षों का औसत उत्पादन किस कंपनी के लिए अधिकतम था? उत्तर: कंपनी X के लिए = [1/5 * (30 + 45 + 25 + 50 + 40)] = 190/5 = 38। कंपनी Y के लिए = [1/5 * (25 + 35 + 35 + 50 + 40)] = 185/5 = 37। कंपनी Z के लिए = [1/5 * (35 + 40 + 45 + 35 + 35)] = 190/5 = 38। पांच वर्षों का औसत उत्पादन दोनों कंपनियों X और Z के लिए अधिकतम है।

कंपनी X के लिए = [1/5 * (30 + 45 + 25 + 50 + 40)] = 190/5 = 38
कंपनी Y के लिए = [1/5 * (25 + 35 + 35 + 50 + 40)] = 185/5 = 37
कंपनी Z के लिए = [1/5 * (35 + 40 + 45 + 35 + 35)] = 190/5 = 38

(v) किस वर्ष में कंपनी Z के उत्पादन का प्रतिशत कंपनी Y के उत्पादन के मुकाबले अधिकतम था? उत्तर: विभिन्न वर्षों में कंपनी Z के उत्पादन का प्रतिशत कंपनी Y के उत्पादन के लिए है: 1996 के लिए = (35/25 * 100)% = 140%।

स्पष्ट है कि यह प्रतिशत 1996 के लिए सबसे अधिक है।

प्रश्न 2: निम्नलिखित चार्ट कुकूलैंड में तकनीकी क्षेत्र में विभिन्न कंपनियों के राजस्व का हिस्सा दर्शाता है: 2001 में, जो कंपनी सबसे तेजी से बढ़ी, उसकी वृद्धि दर 100% थी, उस कंपनी की वृद्धि दर क्या थी जिसकी वृद्धि दर सबसे कम थी? (क) 50% (ख) 25% (ग) 20% (घ) 33%

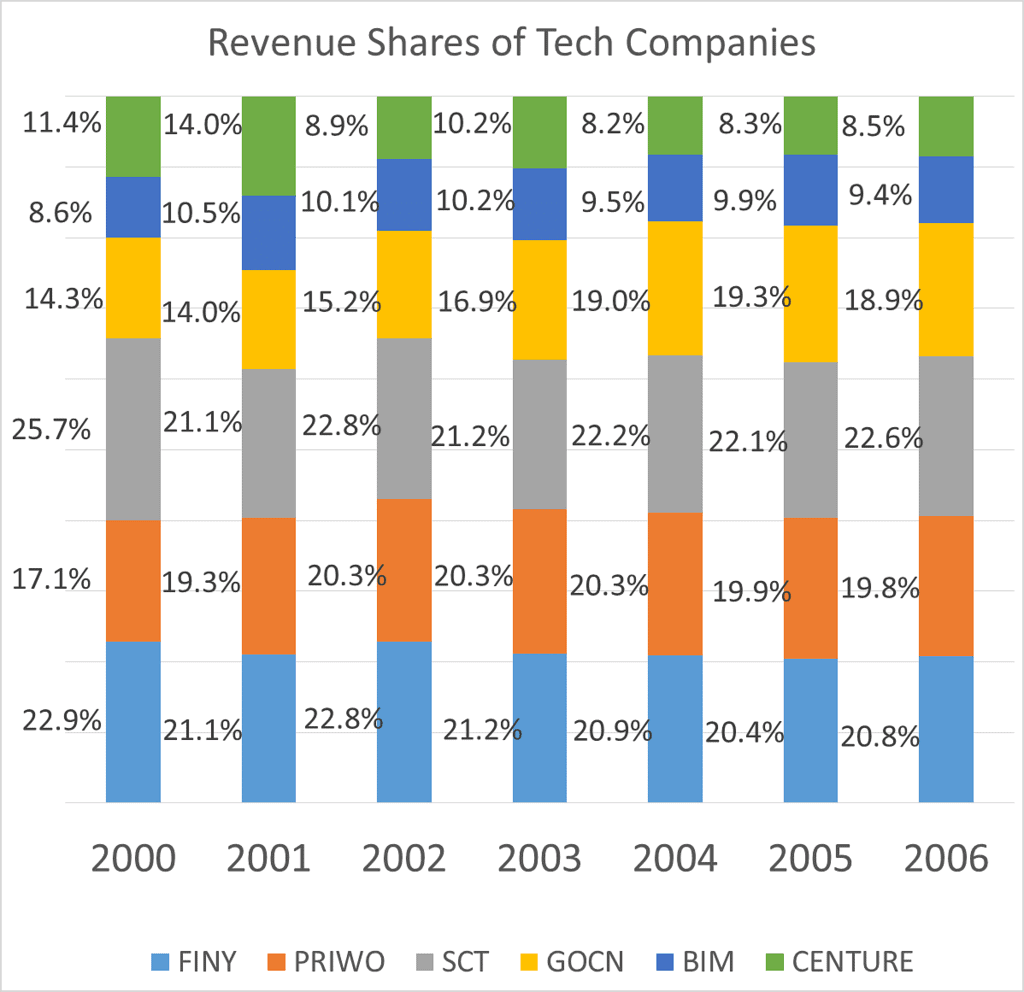
उत्तर: ध्यान दें कि हम इस प्रश्न का उत्तर दे सकते हैं भले ही हमें 2000 और 2001 में कुल आंकड़े ज्ञात न हों। मान लीजिए कि पूरे उद्योग का कुल राजस्व 2000 में X और 2001 में Y है। FINY ने X के 22.9% से Y के 21.1% में वृद्धि की है, जो कि कुछ नहीं बल्कि प्रतिशत के रूप में व्यक्त किया गया है।

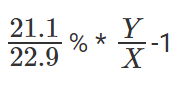
इसी तरह, PRIWO की वृद्धि होगी और बाकी सब के लिए ऐसा ही होगा।

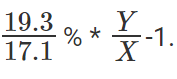
इसलिए, जो कंपनी सबसे तेजी से बढ़ी, वह 2001 के राजस्व हिस्से का 2000 के राजस्व हिस्से के लिए अधिकतम अनुपात रखती थी। केवल हिस्से मायने रखते हैं, X और Y मायने नहीं रखते।

इसलिए, सबसे तेजी से बढ़ने वाली कंपनी का पता लगाने के लिए, हमें केवल सबसे ऊँचा अनुपात ढूँढना है।

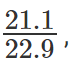
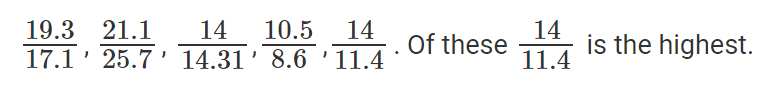
अब, हम जानते हैं कि CENTURE ने सबसे अधिक वृद्धि देखी और यह वृद्धि संख्या 100% थी। या, CENTURE ने अपने राजस्व को दोगुना किया।

या 14% का Y = 11.4% का X * 2 या

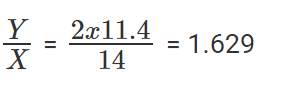
जिस कंपनी ने सबसे कम वृद्धि दर देखी है, हमें सूचीबद्ध अंशों में सबसे कम ढूँढना होगा। या सबसे कम में

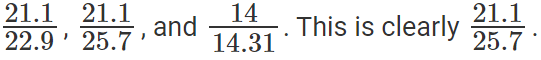
या, जो कंपनी सबसे कम वृद्धि दर देखी है, वह SCT है।

SCT की वृद्धि दर है

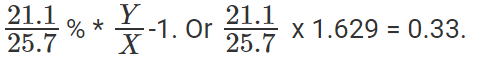
या, SCT ने 33% की वृद्धि की।

प्रश्न है "जिस कंपनी की वृद्धि दर सबसे कम थी?" इसलिए, उत्तर है "33%"। विकल्प (घ) सही उत्तर है।

प्रश्न 3: निम्नलिखित चार्ट में कुकूलैंड में प्रौद्योगिकी क्षेत्र की विभिन्न कंपनियों का राजस्व हिस्सा दिया गया है। :

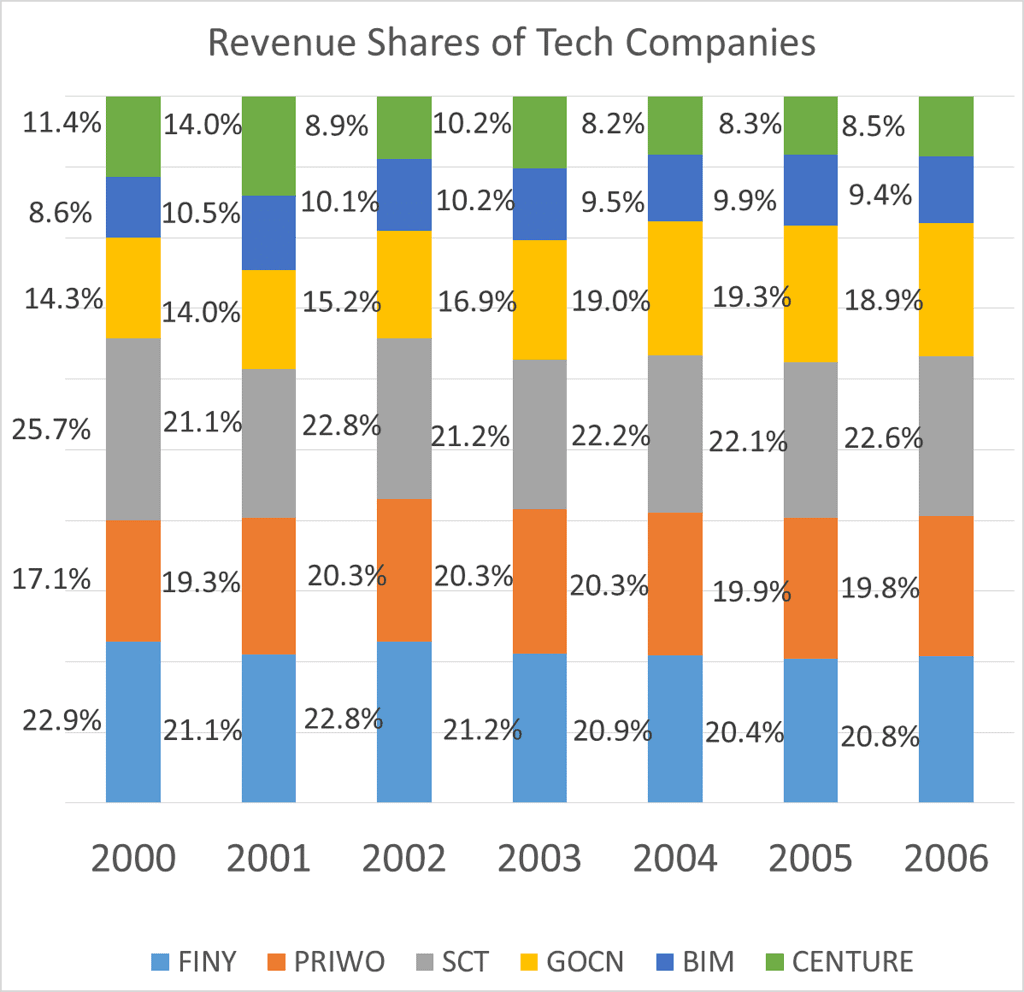
2002 में, समग्र क्षेत्र की वृद्धि दर 39% थी, तो SCT द्वारा देखी गई वृद्धि दर क्या थी? (क) 50% (ख) 75% (ग) 30% (घ) 40%

समाधान: मान लेते हैं कि 2002 का राजस्व Z है, और 2001 का राजस्व Y है। हमें पता है कि Z/Y = 1.39।

SCT की वृद्धि दर को प्रतिशत के रूप में व्यक्त किया गया है।

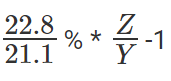
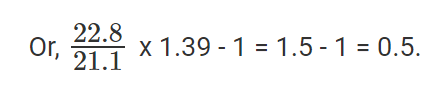
यहाँ 50% की वृद्धि दर थी। प्रश्न है "SCT द्वारा देखी गई वृद्धि दर क्या थी?" इसलिए, उत्तर है "50%"। विकल्प (क) सही उत्तर है।

The document बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA is a part of the RRB NTPC/ASM/CA/TA Course Mathematics for RRB NTPC (Hindi).

All you need of RRB NTPC/ASM/CA/TA at this link: RRB NTPC/ASM/CA/TA

	Mathematics for RRB NTPC (Hindi) 142 videos\|172 docs\|185 tests

Mathematics for RRB NTPC (Hindi)

142 videos|172 docs|185 tests

Join Course for Free

About this Document

Oct 18, 2025 Last updated

Related Exams

RRB NTPC/ASM/CA/TA Bank Exams SSC JE SSC CGL

Document Description: बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) for RRB NTPC/ASM/CA/TA 2025 is part of Mathematics for RRB NTPC (Hindi) preparation. The notes and questions for बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) have been prepared according to the RRB NTPC/ASM/CA/TA exam syllabus. Information about बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) covers topics like and बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) Example, for RRB NTPC/ASM/CA/TA 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ).

Introduction of बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) in English is available as part of our Mathematics for RRB NTPC (Hindi) for RRB NTPC/ASM/CA/TA & बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) in Hindi for Mathematics for RRB NTPC (Hindi) course. Download more important topics related with notes, lectures and mock test series for RRB NTPC/ASM/CA/TA Exam by signing up for free. RRB NTPC/ASM/CA/TA: बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

Description

Full syllabus notes, lecture & questions for बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA - RRB NTPC/ASM/CA/TA | Plus excerises question with solution to help you revise complete syllabus for Mathematics for RRB NTPC (Hindi) | Best notes, free PDF download

Information about बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ)

In this doc you can find the meaning of बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) defined & explained in the simplest way possible. Besides explaining types of बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) theory, EduRev gives you an ample number of questions to practice बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) tests, examples and also practice RRB NTPC/ASM/CA/TA tests

	Mathematics for RRB NTPC (Hindi) 142 videos\|172 docs\|185 tests

Mathematics for RRB NTPC (Hindi)

142 videos|172 docs|185 tests

Join Course for Free

Download as PDF

Explore Courses for RRB NTPC/ASM/CA/TA exam

ppt

बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

Previous Year Questions with Solutions

Extra Questions

Semester Notes

study material

mock tests for examination

MCQs

past year papers

practice quizzes

Viva Questions

Important questions

pdf

video lectures

बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

Exam

Summary

बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

Sample Paper

shortcuts and tricks

Free

Objective type Questions

;

Additional Information about बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) for RRB NTPC/ASM/CA/TA Preparation

बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) Free PDF Download

The बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) is an invaluable resource that delves deep into the core of the RRB NTPC/ASM/CA/TA exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) now and kickstart your journey towards success in the RRB NTPC/ASM/CA/TA exam.

Importance of बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ)

The importance of बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) cannot be overstated, especially for RRB NTPC/ASM/CA/TA aspirants. This document holds the key to success in the RRB NTPC/ASM/CA/TA exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) Notes

बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ). It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) Notes on EduRev are your ultimate resource for success.

बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) RRB NTPC/ASM/CA/TA Questions

The "बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) RRB NTPC/ASM/CA/TA Questions" guide is a valuable resource for all aspiring students preparing for the RRB NTPC/ASM/CA/TA exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) on the App

Students of RRB NTPC/ASM/CA/TA can study बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ), students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of बार ग्राफ: परिचय और उदाहरण (समाधानों के साथ) is prepared as per the latest RRB NTPC/ASM/CA/TA syllabus.

Education Revolution