ध्यान देने योग्य बिंदु: वर्ग और वर्गमूल | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

पूर्ण वर्ग क्या है?

एक प्राकृतिक संख्या n पूर्ण वर्ग है यदि n = m², जहाँ m एक प्राकृतिक संख्या है। इसलिए, जब एक संख्या दूसरी संख्या का वर्ग होती है, तो इसे पूर्ण वर्ग कहा जाता है! उदाहरण: 9 = 3² (3 का वर्ग 9 है) 25 = 5² (5 का वर्ग 25 है)

• यदि एक संख्या 2, 3, 7, या 8 पर समाप्त होती है, तो यह कभी भी पूर्ण वर्ग नहीं हो सकती।
• सम संख्याओं के वर्ग सम होते हैं, और विषम संख्याओं के वर्ग विषम होते हैं।
• एक संख्या जो विषम संख्या के अंशों में समाप्त होती है, वह पूर्ण वर्ग नहीं हो सकती।

दो वर्गों के बीच:

• n² और (n + 1)² के बीच में ठीक 2n गैर-पूर्ण वर्ग संख्याएँ होती हैं!

पाइथागोरियन त्रिकुट संबंध:

• किसी भी प्राकृतिक संख्या n के लिए जो 1 से बड़ी है, संख्याएँ 2n, (n² - 1), और (n² + 1) एक पाइथागोरियन त्रिकुट बनाती हैं।

वर्गमूल:

वर्गमूल एक संख्या के वर्ग करने का विपरीत होता है! उदाहरण: यदि आप 4 का वर्ग करते हैं, तो आपको 16 मिलता है। यदि आप 16 का वर्गमूल लेते हैं, तो आपको 4 मिलता है।

वर्ग संख्याओं में अंकों की संख्या:

• यदि एक संख्या n में n अंक हैं, तो उसके वर्गमूल में अंकों की संख्या होगी:
• n/2 यदि n सम है।
• (n + 1)/2 यदि n विषम है।

संख्या का वर्ग:

जब आप एक संख्या को स्वयं से गुणा करते हैं, तो इसे उस संख्या का वर्ग करना कहा जाता है। उदाहरण: 3 × 3 = 9 (इसका मतलब है कि 9, 3 का वर्ग है!) 5 × 5 = 25 (इसका मतलब है कि 25, 5 का वर्ग है!)

पूर्ण वर्ग:

एक संख्या जैसे 16, जिसे 4² के रूप में व्यक्त किया जा सकता है, उसे पूर्ण वर्ग कहा जाता है! लेकिन याद रखें, हर संख्या पूर्ण वर्ग नहीं होती। उदाहरण के लिए, 32 एक वर्ग संख्या नहीं है। इसलिए, हमेशा जांचें कि क्या एक संख्या दूसरी संख्या का वर्ग है।

याद रखें:

• सभी प्राकृतिक संख्याएँ पूर्ण वर्ग या वर्ग संख्याएँ नहीं होती हैं, 32 एक वर्ग संख्या नहीं है।
• आम तौर पर, यदि एक प्राकृतिक संख्या ‘m’ को n² के रूप में व्यक्त किया जा सकता है, जहाँ n भी एक प्राकृतिक संख्या है, तो ‘m’ पूर्ण वर्ग है।
• संख्याएँ जैसे 1, 4, 9, 16, 25, और 36 को वर्ग संख्याएँ कहा जाता है।

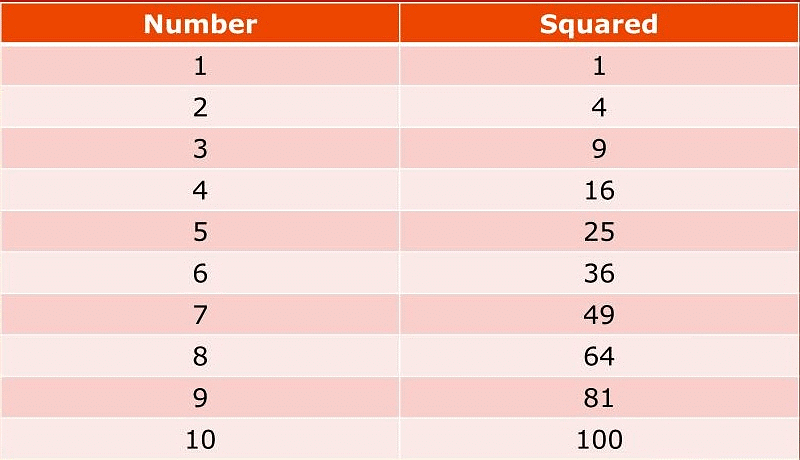
तालिका:

1 से 10 तक की संख्याओं का वर्ग।

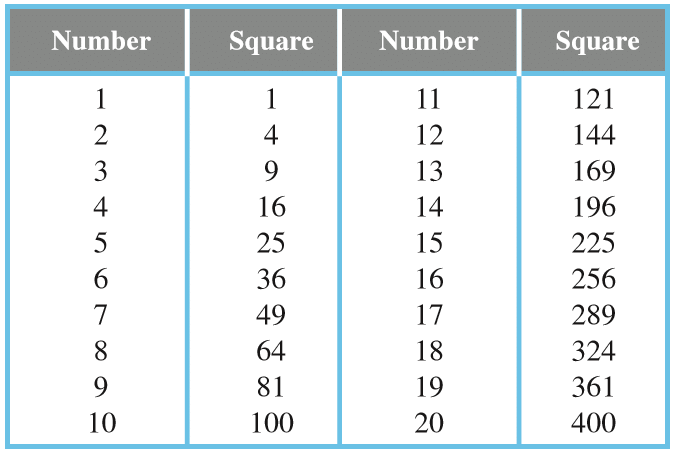
वर्ग संख्या के गुण:

1 से 20 तक की सभी प्राकृतिक संख्याओं के वर्गों पर विचार करें। तालिका से, हम निष्कर्ष निकालते हैं:

• गुण 1: “एक वर्ग संख्या के अंतिम अंक (एक के स्थान में अंक) केवल 0, 1, 4, 5, 6 या 9 होते हैं।”

कुछ दिलचस्प पैटर्न:

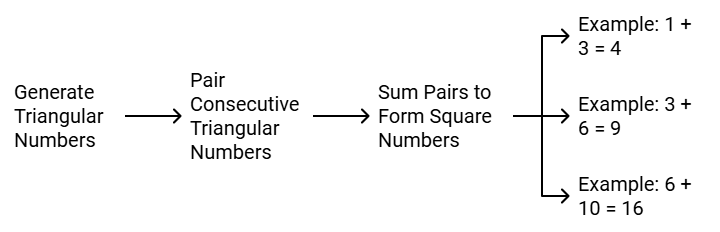
• त्रिकोणीय संख्याएँ हैं: 1, 3, 6, 10, 15, 21, आदि। यदि हम दो लगातार त्रिकोणीय संख्याओं को जोड़ते हैं, तो हमें एक वर्ग संख्या मिलती है।
• 1 + 3 = 4, ‘4’ एक वर्ग संख्या है
• 3 + 6 = 9, ‘9’ एक वर्ग संख्या है
• 6 + 10 = 16, ‘16’ एक वर्ग संख्या है और इसी तरह।

हल किए गए उदाहरण:

उदाहरण 1: निम्नलिखित संख्याओं के वर्ग में एकक अंक क्या होगा?

• 12487
• 1324
• 91478
• 1251

समाधान: निम्नलिखित के वर्ग में एकक अंक हैं:

• 12487 का वर्ग 9 है (क्योंकि 7² = 49, एकक स्थान पर 9 है)।
• 1324 का वर्ग 6 है (क्योंकि 2² = 4, एकक स्थान पर 6 है)।
• 91478 का वर्ग 4 है (क्योंकि 8² = 64, एकक स्थान पर 4 है)।
• 1251 का वर्ग 1 है (क्योंकि 1² = 1, एकक स्थान पर 1 है)।

उदाहरण 2: एक सम और विषम संख्या के वर्ग पर टिप्पणी करें।

समाधान: एक सम संख्या का वर्ग हमेशा एक सम संख्या होता है और एक विषम संख्या का वर्ग हमेशा एक विषम संख्या होता है। एक सम संख्या का वर्ग हमेशा अपने एकक स्थान पर 4, 6, या शून्य अंक रखेगा। और एक विषम संख्या का वर्ग हमेशा 1, 5, या 9 अपने एकक स्थान पर रखेगा।

हल किए गए उदाहरण उदाहरण 1: निम्नलिखित संख्याओं के वर्ग में इकाई का अंक क्या होगा? 1. 12487 2. 1324 3. 91478 4. 1251

हल. एक सम संख्या का वर्ग हमेशा एक सम संख्या होता है और एक विषम संख्या का वर्ग हमेशा एक विषम संख्या होता है। एक सम संख्या का वर्ग हमेशा अपने इकाई स्थान पर 4, 6, या यहां तक कि 0 रखता है। और एक विषम संख्या का वर्ग हमेशा अपने इकाई स्थान पर 1, 5, या 9 रखता है।