महत्वपूर्ण सूत्र: वर्गमूल और घनमूल | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download
वर्गमूल
यदि x2 = y, तो हम कहते हैं कि y का वर्गमूल x है और हम इसे इस प्रकार लिखते हैं: √y = x। इस प्रकार, √4 = 2, √9 = 3, √196 = 14।
घनमूल
किसी दिए गए संख्या x का घनमूल वह संख्या है, जिसका घन x है। हम x के घनमूल को इस प्रकार दर्शाते हैं: ∛x। इस प्रकार, 8 = 2 × 2 × 2 = 2, 343 = 7 × 7 × 7 = 7 आदि।
नोट:
- √xy = √x × √y
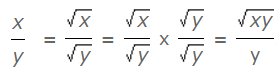
उदाहरण
- उदाहरण 1: (√625 × 14 × 11 के बराबर है: 11 √25 √196) (a) 5 (b) 6 (c) 8 (d) 11 उत्तर: (a) दी गई अभिव्यक्ति
- उदाहरण 2: कितने दो अंकों की संख्याएँ इस गुण को संतुष्ट करती हैं। दो अंकों की संख्या के वर्ग का अंतिम अंक (इकाई का अंक) 8 है? (a) 1 (b) 2 (c) 3 (d) इनमें से कोई नहीं उत्तर: (d) 8 से समाप्त होने वाली संख्या कभी भी पूर्ण वर्ग नहीं हो सकती।
- उदाहरण 3: (a) 10 (b) 100 (c) 1000 (d) इनमें से कोई नहीं उत्तर: (b) तब, 0.0169x = (1.3)2 = 1.69 ⇒ x = 1.69/0.0169 = 100
- उदाहरण 4: यदि √5 = 2.236; तो का मान होगा: (a) 5.59 (b) 7.826 (c) 8.944 (d) 10.062 उत्तर: (b)
- उदाहरण 5: (7 + 3√5) (7 - 3√5) का वर्गमूल है (a) 2 (b) 4 (c) √5 (d) 3√5 उत्तर: (a)
- उदाहरण 6: समीकरण में दोनों x के स्थान पर क्या आना चाहिए: (a) 12 (b) 14 (c) 144 (d) 196 उत्तर: (a) = 8 × 6 × 3 = 144। ∴ x = √144 = 12।
- उदाहरण 7: 0.000216 का घनमूल है: (a) 0.6 (b) 0.06 (c) 77 (d) 87 उत्तर: (b) = 6/102 = 6/100 = 0.06
- उदाहरण 8: सबसे छोटा पूर्ण वर्ग, जो 21, 36 और 66 में से प्रत्येक से विभाज्य है: (a) 213444 (b) 214344 (c) 214434 (d) 231444 उत्तर: (a) 21, 36, 66 का L.C.M. = 2772। अब, 2772 = 2 × 2 × 3 × 3 × 7 × 11 इसे पूर्ण वर्ग बनाने के लिए, इसे 7 × 11 से गुणन करना होगा। तो, आवश्यक संख्या = 22 × 32 × 72 × 112 = 213444।
- उदाहरण 9: यदि a = 0.1039, तो का मान होगा: (a) 0.1039 (b) 0.2078 (c) 1.1039 (d) 2.1039 उत्तर: (c) = (1 - 2a)3a = (1 + a) = (1 + 0.1039) = 1.1039
- उदाहरण 10: छात्रों के एक समूह ने समूह के प्रत्येक सदस्य से उतने पैसे इकट्ठा करने का निर्णय लिया, जितने सदस्य हैं। यदि कुल संग्रह ₹ 59.29 है, तो समूह में सदस्यों की संख्या है: (a) 57 (b) 67 (c) 77 (d) 87 उत्तर: (c) इकट्ठा किया गया धन = (59.29 × 100) पैसे = 5929 पैसे। सदस्यों की संख्या = √5929 = 77।
उदाहरण 2: कितने दो अंकों की संख्याएँ इस गुण को संतुष्ट करती हैं। दो अंकों की संख्या के वर्ग का अंतिम अंक (इकाई का अंक) 8 है? (क) 1 (ख) 2 (ग) 3 (घ) इनमें से कोई नहीं उत्तर: (घ) 8 से समाप्त होने वाला कोई भी संख्या कभी पूर्ण वर्ग नहीं हो सकता।
उदाहरण 3: (क) 10 (ख) 100 (ग) 1000 (घ) इनमें से कोई नहीं उत्तर: (ख) तब, 0.0169x = (1.3)² = 1.69 ⇒ x = 1.69/0.0169 = 100
उदाहरण 4: यदि √5 = 2.236; तो का मान है: (क) 5.59 (ख) 7.826 (ग) 8.944 (घ) 10.062 उत्तर: (ख)
उदाहरण 5: (7 - 3√5) का वर्गमूल (7 + 3√5) है (क) 2 (ख) 4 (ग) √5 (घ) 3√5 उत्तर: (क)
उदाहरण 6: समीकरण में दोनों x के स्थान पर क्या आना चाहिए: (क) 12 (ख) 14 (ग) 144 (घ) 196 उत्तर: (क) = 8 x 6 x 3 = 144। ∴ x = √144 = 12।
उदाहरण 7: .000216 का घनमूल है: (क) .6 (ख) .06 (ग) 77 (घ) 87 उत्तर: (ख) = 6/102 = 6/100 = 0.06
उदाहरण 8: सबसे छोटा पूर्ण वर्ग, जो 21, 36 और 66 में से प्रत्येक से विभाज्य है: (क) 213444 (ख) 214344 (ग) 214434 (घ) 231444 उत्तर: (क) 21, 36, 66 का L.C.M. = 2772। अब, 2772 = 2 x 2 x 3 x 3 x 7 x 11 इसे पूर्ण वर्ग बनाने के लिए, इसे 7 x 11 से गुणा करना होगा। तो, आवश्यक संख्या = 22 x 32 x 72 x 112 = 213444।
उदाहरण 9: यदि a = 0.1039, तो का मान है: (क) 0.1039 (ख) 0.2078 (ग) 1.1039 (घ) 2.1039 उत्तर: (ग) = (1 - 2a) 3a = (1 a) = (1 0.1039) = 1.1039
उदाहरण 10: एक छात्र समूह ने तय किया कि वे समूह के प्रत्येक सदस्य से उतने पैसे इकट्ठा करेंगे जितने सदस्य हैं। यदि कुल संग्रह ₹ 59.29 है, तो समूह में सदस्यों की संख्या है: (क) 57 (ख) 67 (ग) 77 (घ) 87 उत्तर: (ग) इकट्ठा किया गया पैसा = (59.29 x 100) पैसे = 5929 पैसे। सदस्यों की संख्या = √5929 = 77।
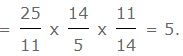
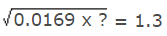
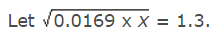
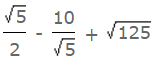
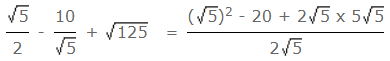
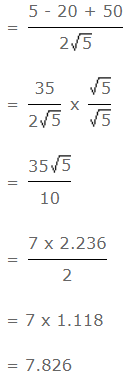
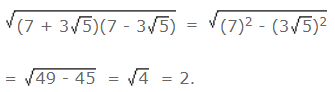
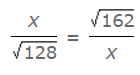
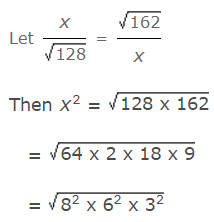
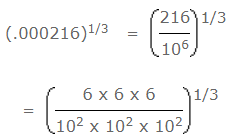
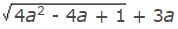
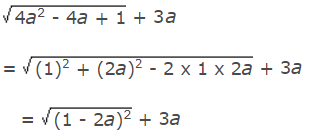
|
142 videos|172 docs|185 tests
|















