महत्वपूर्ण सूत्र: संभाव्यता | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

संभावना क्या है?

संभावना को एक भविष्यवाणीनुमा माप के रूप में देखा जा सकता है, जिसे \"x\" चर द्वारा दर्शाया जाता है, जो किसी घटना के घटित होने की संभावना को प्रदर्शित करता है, जबकि (1-x) घटना के न होने की संभावनाओं के लिए है। संभावना सूत्र किसी घटना के किसी यादृच्छिक प्रयोग में घटित होने की संभावना की गणना करने के लिए कार्य करता है।

• संभावना या अवसर: संभावना या अवसर एक सामान्य शब्द है जिसका उपयोग दैनिक जीवन में किया जाता है। उदाहरण: हम सामान्यतः कहते हैं, 'आज बारिश हो सकती है'। इस वाक्य में कुछ निश्चित अनिश्चितता है। संभावना एक विशेष घटना के घटित होने के अवसर का मात्रात्मक माप है।

संभावना या अवसर: संभावना या अवसर एक सामान्य शब्द है जिसका उपयोग दैनिक जीवन में किया जाता है। उदाहरण: हम सामान्यतः कहते हैं, 'आज बारिश हो सकती है'। इस वाक्य में कुछ निश्चित अनिश्चितता है। संभावना एक विशेष घटना के घटित होने के अवसर का मात्रात्मक माप है।

• प्रयोग: एक प्रयोग एक ऐसा संचालन है जो स्पष्ट परिणाम उत्पन्न कर सकता है।

प्रयोग: एक प्रयोग एक ऐसा संचालन है जो स्पष्ट परिणाम उत्पन्न कर सकता है।

• यादृच्छिक प्रयोग: यदि किसी प्रयोग के सभी संभावित परिणाम ज्ञात हैं लेकिन सही आउटपुट को पूर्वानुमानित नहीं किया जा सकता, तो उस प्रयोग को यादृच्छिक प्रयोग कहा जाता है। उदाहरण:
  • समान सिक्का उछालना: जब हम एक सिक्का उछालते हैं, तो परिणाम या तो सिर (H) या पूंछ (T) होगा।
  • निष्पक्ष पासा फेंकना: पासा एक छोटा घन है जो खेलों में उपयोग किया जाता है। इसके छह चेहरे होते हैं और प्रत्येक चेहरे पर 1 से 6 तक विभिन्न बिंदुओं की संख्या होती है। पासे का बहुवचन पासे है। जब पासा फेंका या घुमाया जाता है, तो परिणाम उस पर के ऊपरी चेहरे पर दिखाई देने वाली संख्या होती है और यह 1 से 6 के बीच एक यादृच्छिक पूर्णांक है, प्रत्येक मान समान रूप से संभावित है।
  • ताश का एक कार्ड निकालना: ताश के खेल के एक पैक में 52 कार्ड होते हैं जिन्हें चार श्रेणियों में विभाजित किया गया है। प्रत्येक श्रेणी में 13 कार्ड होते हैं, जिनमें 2 से 10 तक के 9 कार्ड, एक एसी, एक राजा, एक रानी और एक जैक शामिल होते हैं। दिल और हीरा लाल रंग के कार्ड हैं जबकि ♠ और ♣ काले रंग के कार्ड हैं। राजा, रानी और जैक को फेस कार्ड कहा जाता है: (i) ♠ (स्पेड्स) (ii) ♣ (क्लब्स) (iii) ♥ (हार्ट्स) (iv) ♦ (डायमंड्स)
  • एक बैग से यादृच्छिक रूप से एक गेंद लेना जिसमें विभिन्न रंगों की गेंदें हैं।

यादृच्छिक प्रयोग: यदि किसी प्रयोग के सभी संभावित परिणाम ज्ञात हैं लेकिन सही आउटपुट को पूर्वानुमानित नहीं किया जा सकता, तो उस प्रयोग को यादृच्छिक प्रयोग कहा जाता है।

एक निष्पक्ष सिक्का उछालना: जब हम एक सिक्का उछालते हैं, तो परिणाम या तो हेड (H) या टेल (T) होगा।

• निष्पक्ष सिक्का उछालना: जब हम एक सिक्का उछालते हैं, तो परिणाम या तो हेड (H) या टेल (T) होगा।
• अनपक्षीय पासा फेंकना: पासा एक छोटा घन होता है जो खेलों में उपयोग किया जाता है। इसके छह चेहरे होते हैं और प्रत्येक चेहरे पर 1 से 6 तक विभिन्न बिंदुओं की संख्या होती है। पासे का बहुवचन डाइस (dice) है। जब पासा फेंका या घुमाया जाता है, तो परिणाम वह संख्या होती है जो इसके ऊपरी चेहरे पर दिखाई देती है, और यह एक यादृच्छिक पूर्णांक (random integer) होता है जो एक से छह के बीच होता है, प्रत्येक मान समान रूप से संभावित होता है।
• shuffled cards के एक पैक से एक कार्ड निकालना: खेल के कार्डों का एक पैक या डेक 52 कार्डों से बना होता है, जो चार श्रेणियों में विभाजित होता है, जैसा कि नीचे दिया गया है। उपरोक्त श्रेणियों में से प्रत्येक में 13 कार्ड होते हैं, 2 से 10 तक के 9 कार्ड होते हैं, एक ऐस, एक राजा, एक रानी और एक जैक। दिल (Hearts) और हीरा (Diamonds) लाल चेहरे वाले कार्ड हैं जबकि स्पेड्स (Spades) और क्लब्स (Clubs) काले चेहरे वाले कार्ड हैं। राजा, रानी, और जैक को फेस कार्ड कहा जाता है:

• स्पेड्स (♠)
• क्लब्स (♣)
• दिल (♥)
• हीरा (♦)
• रंग-बिरंगी गेंदों के बैग से यादृच्छिक रूप से एक गेंद लेना।

शuffled cards से एक कार्ड निकालना: Playing cards का एक pack या deck 52 कार्ड्स का होता है, जिन्हें नीचे दिए गए चार वर्गों में विभाजित किया गया है। उपरोक्त प्रत्येक वर्ग में 13 कार्ड होते हैं, जिनमें 2 से 10 तक के 9 कार्ड, एक Ace, एक King, एक Queen और एक Jack शामिल होते हैं। Hearts और Diamonds लाल रंग के कार्ड होते हैं जबकि Spades और Clubs काले रंग के होते हैं। Kings, Queens और Jacks को face cards कहा जाता है: (i) Spades (♠) (ii) Clubs (♣) (iii) Hearts (♥) (iv) Diamonds (♦)

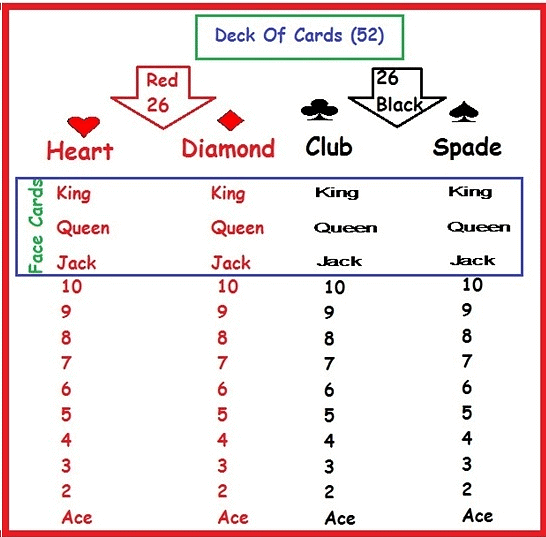
Kings, Queens और Jacks को face cards कहा जाता है: (i) Spades (♠) (ii) Clubs (♣) (iii) Hearts (♥) (iv) Diamonds (♦)

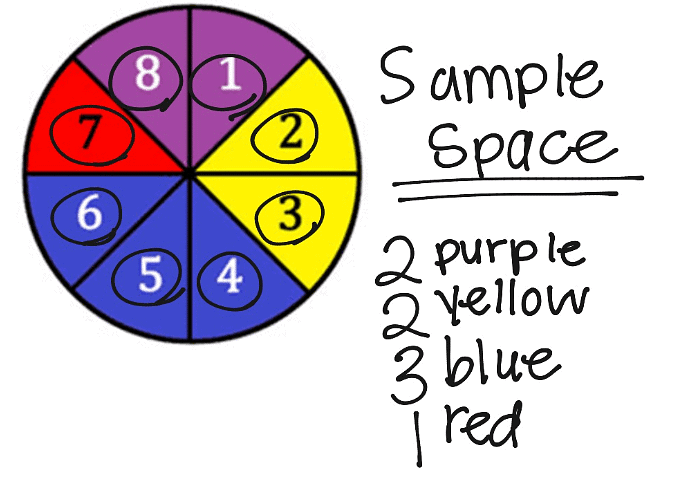
Sample Space: Sample Space एक प्रयोग के सभी संभावित परिणामों का सेट होता है। इसे S द्वारा दर्शाया जाता है।

उदाहरण: (i) जब एक सिक्का उछाला जाता है, S = {H, T} जहां H = Head और T = Tail (ii) जब एक dice फेंका जाता है, S = {1, 2, 3, 4, 5, 6} (iii) जब दो सिक्के उछाले जाते हैं, S = {HH, HT, TH, TT} जहां H = Head और T = Tail

घटना: एक नमूना स्थान का कोई भी उपसमुच्चय एक घटना है। घटनाओं को आमतौर पर बड़े अक्षरों A, B, C, D आदि से दर्शाया जाता है।

• उदाहरण: (i) जब एक सिक्का उछाला जाता है, तो सिर या पूंछ पाने का परिणाम एक घटना है। (ii) जब एक पासा फेंका जाता है, तो 1 या 2 या 3 या 4 या 5 या 6 पाने का परिणाम एक घटना है।

घटना की संभावना: मान लीजिए E एक घटना है और S नमूना स्थान है। तब घटना E की संभावना को इस प्रकार परिभाषित किया जा सकता है:

जहाँ P(E) = घटना E की संभावना, n(E) = घटना के होने के तरीके की संख्या और n(S) = संभावित परिणामों की कुल संख्या है।

P(S) = 1

0 ≤ P (E) ≤ 1

P(ϕ) = 0 (∵ असंभव घटना के होने की संभावना = 0)

(i) एक सिक्का एक बार उछाला जाता है। सिर पाने की संभावना क्या है?

जब एक सिक्का उछाला जाता है, तो संभावित परिणामों की कुल संख्या = n(S) = 2 (∵ सिर या पूंछ)

E = सिर पाने की घटना = {H}। इसलिए n(E) = 1

(ii) दो पासे फेंके जाते हैं। संभावना क्या है कि दोनों पासों के शीर्ष चेहरे का योग 9 से अधिक होगा?

जब एक पासा फेंका जाता है, तो संभावित परिणामों की कुल संख्या = 6 (∵ 6 चेहरों में से कोई एक चेहरा)

इसलिए, जब दो पासे फेंके जाते हैं, तो संभावित परिणामों की कुल संख्या n(S) = 6 × 6 = 36 है।

E = जब दो पासे फेंके जाते हैं, तो 9 से अधिक का योग प्राप्त करना = {(4, 6), {5, 5}, {5, 6}, {6, 4}, {6, 5}, (6, 6)}

अतः, n(E) = 6।

घटनाओं के प्रकार

• समान संभावित घटनाएँ: घटनाएँ समान संभावित कहलाती हैं यदि किसी विशेष घटना के लिए कोई प्राथमिकता नहीं होती है। उदाहरण: (i) जब एक सिक्का उछाला जाता है, तो हेड (H) या टेल समान संभावितता से आ सकता है। (ii) जब एक पासा फेंका जाता है, तो सभी छह चेहरे (1, 2, 3, 4, 5, 6) समान संभावितता से आ सकते हैं।

समान संभावित घटनाएँ: घटनाएँ समान संभावित कहलाती हैं यदि किसी विशेष घटना के लिए कोई प्राथमिकता नहीं होती है।

उदाहरण: (i) जब एक सिक्का उछाला जाता है, तो हेड (H) या टेल समान संभावितता से आ सकता है। (ii) जब एक पासा फेंका जाता है, तो सभी छह चेहरे (1, 2, 3, 4, 5, 6) समान संभावितता से आ सकते हैं।

• एक दूसरे को बाहर करने वाली घटनाएँ: दो या दो से अधिक घटनाएँ एक दूसरे को बाहर करने वाली कहलाती हैं यदि एक घटना का होना दूसरी घटना के होने को बाहर करता है। इसे निम्नलिखित उदाहरणों से बेहतर ढंग से समझाया जा सकता है: नोट: यदि A और B एक दूसरे को बाहर करने वाली घटनाएँ हैं, तो A ∩ B = ϕ जहाँ ϕ को खाली सेट दर्शाता है। (i) जब एक सिक्का उछाला जाता है, तो हमें या तो हेड या टेल मिलता है। हेड और टेल एक साथ नहीं आ सकते। इसलिए हेड और टेल की घटनाएँ एक दूसरे को बाहर करने वाली घटनाएँ हैं। (ii) जब एक पासा फेंका जाता है, तो हमें 1 या 2 या 3 या 4 या 5 या 6 मिलता है। ये सभी चेहरे एक साथ नहीं आ सकते। इसलिए पासा फेंकने पर विशेष चेहरों की घटनाएँ एक दूसरे को बाहर करने वाली घटनाएँ हैं। (iii) मान लीजिए कि एक पासा फेंका गया और A वह घटना है जिसमें 2 या 4 या 6 आता है और B वह घटना है जिसमें 4 या 5 या 6 आता है। तब A = {2, 4, 6} और B = {4, 5, 6}। यहाँ A ∩ B ≠ ϕ। इसलिए A और B एक दूसरे को बाहर करने वाली घटनाएँ नहीं हैं।

एक दूसरे को बाहर करने वाली घटनाएँ: दो या दो से अधिक घटनाएँ एक दूसरे को बाहर करने वाली कहलाती हैं यदि एक घटना का होना दूसरी घटना के होने को बाहर करता है।

नोट: यदि A और B परस्पर विशेष घटनाएँ हैं, तो A ∩ B = ϕ, जहाँ ϕ खाली सेट को दर्शाता है। (i) जब एक सिक्का उछाला जाता है, तो हमें या तो हेड या टेल मिलता है। हेड और टेल एक साथ नहीं आ सकते। इसलिए, हेड और टेल की घटना परस्पर विशेष घटनाएँ हैं। (ii) जब एक पासा फेंका जाता है, तो हमें 1, 2, 3, 4, 5 या 6 में से कोई एक प्राप्त होता है। ये सभी चेहरे एक साथ नहीं आ सकते। इसलिए, पासा फेंकने पर विशेष चेहरों की घटनाएँ परस्पर विशेष घटनाएँ हैं। (iii) मान लें कि एक पासा फेंका गया और A वह घटना है जिसमें 2, 4 या 6 आता है और B वह घटना है जिसमें 4, 5 या 6 आता है। तो A = {2, 4, 6} और B = {4, 5, 6} है। यहाँ A ∩ B ≠ ϕ। इसलिए, A और B परस्पर विशेष घटनाएँ नहीं हैं।

• स्वतंत्र घटनाएँ: घटनाएँ स्वतंत्र कहलाती हैं यदि एक घटना की घटना या न होने का प्रभाव दूसरी घटना की घटना या न होने पर नहीं पड़ता। उदाहरण: जब एक सिक्का दो बार उछाला जाता है, तो पहले उछाल में टेल (T) आने की घटना और दूसरे उछाल में टेल (T) आने की घटना स्वतंत्र घटनाएँ हैं। इसका कारण यह है कि किसी भी उछाल में टेल (T) आने की घटना दूसरी उछाल में टेल (T) आने की घटना को प्रभावित नहीं करती।

स्वतंत्र घटनाएँ: घटनाएँ स्वतंत्र कहलाती हैं यदि एक घटना की घटना या न होने का प्रभाव दूसरी घटना की घटना या न होने पर नहीं पड़ता।

उदाहरण: जब एक सिक्का दो बार उछाला जाता है, तो पहले उछाल में टेल (T) आने की घटना और दूसरे उछाल में टेल (T) आने की घटना स्वतंत्र घटनाएँ हैं। इसका कारण यह है कि किसी भी उछाल में टेल (T) आने की घटना दूसरी उछाल में टेल (T) आने की घटना को प्रभावित नहीं करती।

सरल घटनाएँ: सरल घटनाओं के मामले में, हम एकल घटनाओं के होने की संभाव्यता लेते हैं।

• उदाहरण: (i) जब सिक्का उछाला जाता है, तो Head (H) प्राप्त करने की संभाव्यता। (ii) जब पासा फेंका जाता है, तो 1 प्राप्त करने की संभाव्यता।

संयुक्त घटनाएँ: संयुक्त घटनाओं के मामले में, हम दो या अधिक घटनाओं के संयुक्त होने की संभाव्यता लेते हैं।

• उदाहरण: जब दो सिक्के उछाले जाते हैं, तो पहले उछाल में Head (H) प्राप्त करने और दूसरे उछाल में Tail (T) प्राप्त करने की संभाव्यता।

व्यापक घटनाएँ: व्यापक घटना एक प्रयोग के सभी संभावित परिणामों की कुल संख्या होती है।

• उदाहरण: (i) जब सिक्का उछाला जाता है, तो हमें या तो Head या Tail मिलता है। इसलिए, यहाँ 2 व्यापक घटनाएँ हैं। (ii) जब दो सिक्के उछाले जाते हैं, तो संभावित परिणाम हैं (H, H), (H, T), (T, H), (T, T)। इसलिए, यहाँ 4 (=2²) व्यापक घटनाएँ हैं। (iii) जब पासा फेंका जाता है, तो हमें 1, 2, 3, 4, 5 या 6 मिलता है। इसलिए, यहाँ 6 व्यापक घटनाएँ हैं।

उदाहरण: (i) जब एक सिक्का उछाला जाता है, तो हमें या तो हेड (Head) या टेल (Tail) मिलता है। इसलिए, 2 पूर्ण घटनाएँ हैं। (ii) जब दो सिक्के उछाले जाते हैं, तो संभावित परिणाम (H, H), (H, T), (T, H), (T, T) होते हैं। इसलिए, 4 (=2²) पूर्ण घटनाएँ हैं। (iii) जब एक पासा उछाला जाता है, तो हमें 1, 2, 3, 4, 5 या 6 मिलता है। इसलिए, 6 पूर्ण घटनाएँ हैं।

संघ, छेदन और पूरक

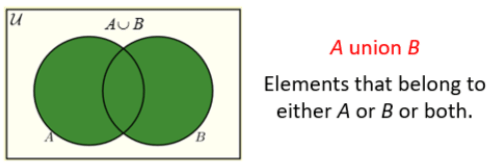
• दो सेटों का संघ (Union) उन सभी तत्वों को शामिल करता है जो या तो पहले सेट में हैं या दूसरे सेट में (या दोनों सेटों में)। संघ को A ⋃ B के रूप में निरूपित किया जाता है।
• दो सेटों का छेदन (Intersection) केवल उन तत्वों को शामिल करता है जो दोनों सेटों में हैं। छेदन को A ⋂ B के रूप में निरूपित किया जाता है।
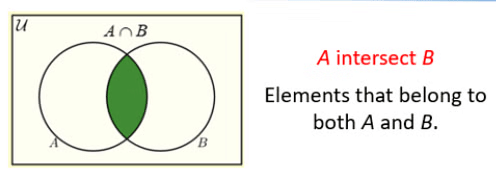
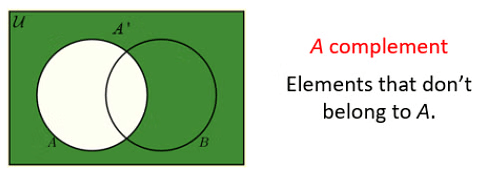
• सेट A का पूरक (Complement) उन सभी चीजों को शामिल करता है जो सेट A में नहीं हैं। पूरक को निम्नलिखित रूप में निरूपित किया जाता है।

उपरोक्त शब्दों के लिए वेन आरेख (Venn Diagrams) निम्नलिखित चित्र में दिखाए गए हैं।

वेन आरेख और सूत्र

घटनाओं का बीजगणित मान लें कि A और B दो घटनाएँ हैं जिनका नमूना क्षेत्र S है। तब

अन्य महत्वपूर्ण गणनाएँ

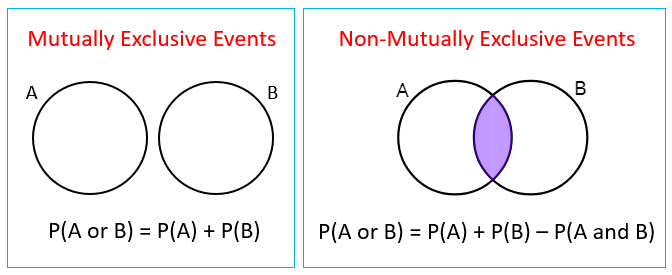
• योग (Addition) प्रमेय: मान लें कि A और B दो घटनाएँ हैं जो एक यादृच्छिक प्रयोग से संबंधित हैं। तब P(A U B) = P(A) + P(B) – P(A ∩ B) यदि A और B पारस्परिक रूप से विशिष्ट घटनाएँ (Mutually Exclusive Events) हैं, तो P(A U B) = P(A) + P(B) क्योंकि पारस्परिक रूप से विशिष्ट घटनाओं के लिए P(A ∩ B) = 0।
• स्वतंत्र घटनाएँ (Independent Events): यदि A और B दो स्वतंत्र घटनाएँ हैं, तो P(A ∩ B) = P(A) × P(B)। उदाहरण: यदि दो पासे उछाले जाते हैं। एक पासे पर विषम संख्या (Odd Number) आने और दूसरे पासे पर सम संख्या (Even Number) आने की संभावना क्या है? एक पासे के उछालने पर संभावित परिणामों की कुल संख्या, n(S) = 6 (क्योंकि 6 में से कोई एक चेहरा)। मान लें A वह घटना है जिसमें एक पासे पर विषम संख्या आती है = {1, 3, 5}। => n(A) = 3 मान लें B वह घटना है जिसमें दूसरे पासे पर सम संख्या आती है = {2, 4, 6}। => n(B) = 3 आवश्यक संभावना, P(A ∩ B) = P(A) × P(B) =। यदि A कोई घटना है और A¯ उसकी पूरक घटना है (अर्थात, A¯ वह घटना है जो A नहीं होती)। तब

स्वतंत्र घटनाएँ: यदि A और B दो स्वतंत्र घटनाएँ हैं, तब

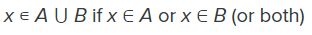
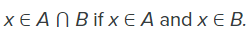
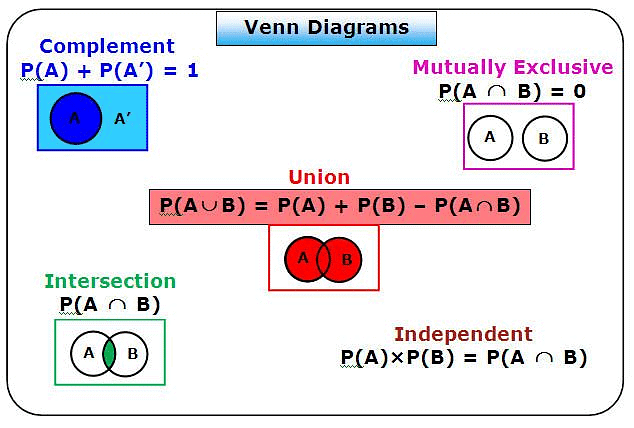
P(A ∩ B) = P(A).P(B)

मान लीजिए कि A कोई घटना है और A¯ इसकी पूरक घटना है (अर्थात, A¯ वह घटना है जिसमें A नहीं होती)। तब

• घटना पर संभावना मान लीजिए E एक घटना है जो एक यादृच्छिक प्रयोग से संबंधित है। मान लीजिए कि x परिणाम E के लिए अनुकूल हैं और y परिणाम E के लिए अनुकूल नहीं हैं, तब उदाहरण: जब एक पासा फेंका जाता है, तब 1 आने की संभावना और इसके खिलाफ क्या है? मान लीजिए E वह घटना है जिसमें एक पासा फेंकने पर 1 आता है। E के लिए अनुकूल परिणाम, x=1 E के लिए अनुकूल नहीं परिणाम, y=5

मान लीजिए E एक घटना है जो एक यादृच्छिक प्रयोग से संबंधित है। मान लीजिए कि x परिणाम E के लिए अनुकूल हैं और y परिणाम E के लिए अनुकूल नहीं हैं, तब

E के लिए अनुकूल परिणाम, x=1

E के लिए अनुकूल नहीं परिणाम, y=5

सशर्त संभावना

मान लीजिए A और B दो घटनाएँ हैं जो एक यादृच्छिक प्रयोग से संबंधित हैं। तब, A की होने की संभावना, यह मानते हुए कि B पहले ही हो चुकी है, उसे सशर्त संभावना कहा जाता है और इसे P(A/B) द्वारा दर्शाया जाता है।

उदाहरण: एक थैला में 5 काले और 4 नीले गेंदें हैं। थैले से एक-एक करके दो गेंदें बिना प्रतिस्थापन के निकाली जाती हैं। यदि पहली बार एक काली गेंद निकाली गई है, तो दूसरी बार नीली गेंद निकालने की संभावना क्या है?

हल: मान लीजिए A पहली बार काली गेंद निकालने की घटना है और B दूसरी बार नीली गेंद निकालने की घटना है। तब, P(B/A) = दूसरी बार नीली गेंद निकालने की संभावना, यह मानते हुए कि पहली बार एक काली गेंद निकाली गई है।

कुल गेंदें = 5 + 4 = 9

चूंकि एक काली गेंद पहले ही निकाली जा चुकी है,

पहली ड्रॉ के बाद कुल गेंदों की संख्या = 8

पहली ड्रॉ के बाद नीली गेंदों की कुल संख्या = 4

बाइनोमियल प्रॉबेबिलिटी वितरण

एक बाइनोमियल प्रयोग एक प्रॉबेबिलिटी प्रयोग है जो निम्नलिखित आवश्यकताओं को पूरा करता है:

• (i) प्रत्येक परीक्षण में केवल दो परिणाम हो सकते हैं। इन परिणामों को सफलता या विफलता के रूप में माना जा सकता है।
• (ii) परीक्षणों की संख्या निश्चित होनी चाहिए।
• (iii) प्रत्येक परीक्षण के परिणाम एक-दूसरे से स्वतंत्र होने चाहिए।
• (iv) प्रत्येक परीक्षण में सफलता की संभावना समान रहनी चाहिए।

एक बाइनोमियल प्रयोग में, n परीक्षणों में ठीक r सफलताओं को प्राप्त करने की संभावना दी जा सकती है:

जहाँ p = एक परीक्षण में सफलता की संभावना, q = 1 - p = एक परीक्षण में विफलता की संभावना

नोट: यदि n निष्पक्ष सिक्के उछाले जाते हैं, तो नमूना स्थान में कुल संभावित परिणामों की संख्या = 2ⁿ है।

• जब n सिक्के उछाले जाते हैं, तो ठीक r संख्या के सिर प्राप्त करने की संभावना =