सारांश: सांख्यिकी और संभावना | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download
सांख्यिकी
- सांख्यिकी को सबसे सरल रूप में डेटा की जांच और हेरफेर के रूप में वर्णित किया जा सकता है।
- जैसा कि पहले चर्चा की गई थी, सांख्यिकी का मुख्य ध्यान संख्यात्मक डेटा के विश्लेषण और गणना पर केंद्रित है।
- आइए विभिन्न लेखकों द्वारा दी गई सांख्यिकी की परिभाषाओं पर चर्चा करें।
- मेरियम-वेबस्टर डिक्शनरी के अनुसार, सांख्यिकी को इस प्रकार परिभाषित किया जा सकता है: "संविधानात्मक जानकारी जो एक विशेष क्षेत्र में जनसंख्या की स्थितियों का प्रतिनिधित्व करती है, विशेष रूप से जानकारी जिसे संख्यात्मक या अन्य संरचित प्रारूपों में व्यक्त किया जा सकता है।"
- प्रसिद्ध सांख्यिकीज्ञ सर आर्थर लियोन बॉवली सांख्यिकी को इस प्रकार परिभाषित करते हैं: "किसी भी शोध क्षेत्र से तथ्यों के संख्यात्मक बयान, जिन्हें एक-दूसरे के साथ संबंध में रखा जाता है।"
सांख्यिकी के उदाहरण
सांख्यिकी के कुछ वास्तविक जीवन के उदाहरण हैं:
- कक्षा में 50 छात्रों द्वारा प्राप्त अंकों का औसत निकालना। यहाँ औसत मान प्राप्त अंकों की सांख्यिकी है।
- मान लीजिए कि आपको यह जानना है कि एक शहर में कितने सदस्य कार्यरत हैं। चूंकि शहर की जनसंख्या 15 लाख है, इसलिए हम यहाँ 1000 लोगों (नमूना) का सर्वेक्षण करेंगे। इसके आधार पर, हम डेटा बनाएंगे, जो सांख्यिकी है।
सांख्यिकी की मूल बातें
- सांख्यिकी की मूल बातें केंद्रीय प्रवृत्ति और फैलाव के माप में शामिल हैं।
- केंद्रीय प्रवृत्तियाँ हैं: औसत (mean), माध्य (median), और मोड (mode); और फैलाव में वेरिएंस (variance) और मानक विचलन (standard deviation) शामिल होते हैं।
- औसत अवलोकनों का औसत होता है।
- माध्य वह केंद्रीय मान होता है जब अवलोकनों को क्रम में व्यवस्थित किया जाता है।
- मोड डेटा सेट में सबसे बार-बार आने वाले अवलोकनों को निर्धारित करता है।
- वेरिएशन डेटा के संग्रह के फैलाव का माप है।
- मानक विचलन औसत से डेटा के फैलाव का माप है।
- मानक विचलन का वर्ग वेरिएंस के बराबर होता है।
गणितीय सांख्यिकी
गणितीय सांख्यिकी गणित का सांख्यिकी पर अनुप्रयोग है, जिसे प्रारंभ में राज्य के विज्ञान के रूप में सोचा गया था — एक देश के बारे में तथ्यों का संग्रह और विश्लेषण: इसकी अर्थव्यवस्था, सैन्य, जनसंख्या, आदि। विभिन्न विश्लेषणों के लिए उपयोग की जाने वाली गणितीय तकनीकों में गणितीय विश्लेषण, रेखीय बीजगणित, स्टोकास्टिक विश्लेषण, अवकल समीकरण और माप-थ्योरी आधारित संभाव्यता सिद्धांत शामिल हैं।
सांख्यिकी के प्रकार
आधारभूत रूप से, सांख्यिकी के दो प्रकार हैं।
- वर्णनात्मक सांख्यिकी
- अनुमानात्मक सांख्यिकी
वर्णनात्मक सांख्यिकी के मामले में, डेटा या डेटा का संग्रह संक्षेप में वर्णित किया जाता है। लेकिन अनुमानात्मक सांख्यिकी के मामले में, इसका उपयोग वर्णनात्मक सांख्यिकी को समझाने के लिए किया जाता है। इन दोनों प्रकारों का बड़े पैमाने पर उपयोग किया गया है।
वर्णनात्मक सांख्यिकी में डेटा को संक्षेपित और समझाया जाता है। संक्षेपण एक जनसंख्या नमूने से किया जाता है, जिसमें कई कारकों जैसे औसत और मानक विचलन का उपयोग किया जाता है। वर्णनात्मक सांख्यिकी डेटा के एक सेट को चार्ट, ग्राफ़ और संक्षेप उपायों के माध्यम से व्यवस्थित, प्रस्तुत और समझाने का एक तरीका है। हिस्टोग्राम, पाई चार्ट, बार, और स्कैटर प्लॉट डेटा को संक्षेपित करने और इसे तालिकाओं या ग्राफ़ में प्रस्तुत करने के सामान्य तरीके हैं। वर्णनात्मक सांख्यिकी केवल वर्णनात्मक होती हैं: इन्हें उस डेटा से परे सामान्यीकृत करने की आवश्यकता नहीं होती है जो वे एकत्र करते हैं।
हम वर्णनात्मक सांख्यिकी के अर्थ को अनुमानात्मक सांख्यिकी का उपयोग करके समझने का प्रयास करते हैं। हम एकत्रित डेटा के अर्थ को संप्रेषित करने के लिए अनुमानात्मक सांख्यिकी का उपयोग करते हैं, जब इसे एकत्र किया गया, मूल्यांकित किया गया, और संक्षेपित किया गया हो। अनुमानात्मक सांख्यिकी में संभाव्यता सिद्धांत का उपयोग इस बात को निर्धारित करने के लिए किया जाता है कि किसी अध्ययन नमूने में पाए गए पैटर्न को उस व्यापक जनसंख्या पर लागू किया जा सकता है, जिससे नमूना लिया गया था। अनुमानात्मक सांख्यिकी का उपयोग परिकल्पनाओं का परीक्षण करने और चर के बीच संबंधों का अध्ययन करने के लिए किया जाता है, और इसका उपयोग जनसंख्या के आकार की भविष्यवाणी करने के लिए भी किया जा सकता है। अनुमानात्मक सांख्यिकी का उपयोग नमूनों से निष्कर्ष और अनुमान निकालने के लिए किया जाता है, अर्थात्, सटीक सामान्यीकरण बनाने के लिए।
सांख्यिकी सूत्र
सांख्यिकीय विश्लेषण में सामान्यतः उपयोग किए जाने वाले सूत्र नीचे दिए गए तालिका में प्रस्तुत हैं।

सारांश सांख्यिकी
सांख्यिकी में, सारांश सांख्यिकी वर्णात्मक सांख्यिकी का एक भाग है (जो सांख्यिकी के प्रकारों में से एक है), जो नमूना डेटा के बारे में जानकारी की सूची प्रदान करता है। हम जानते हैं कि सांख्यिकी डेटा को दृश्य रूप से और मात्रात्मक रूप से प्रस्तुत करने से संबंधित है। इस प्रकार, सारांश सांख्यिकी सांख्यिकीय जानकारी को संक्षेपित करने का कार्य करती है। सारांश सांख्यिकी सामान्यतः डेटा को एक सरल रूप में संक्षेपित करने का प्रयास करती है, ताकि पर्यवेक्षक एक नज़र में जानकारी को समझ सके। सामान्यतः, सांख्यिकीविद् अवलोकनों का वर्णन करने के लिए निम्नलिखित खोजने का प्रयास करते हैं:
- केंद्र प्रवृत्ति या स्थानों का गणितीय औसत।
- वितरण आकृतियों का स्क्यूनेस या कुर्तोसिस।
- विखंडन का मानक औसत अपसामान्य विचलन।
- सांख्यिकीय निर्भरता का सहसंबंध गुणांक।
सारांश सांख्यिकी तालिका
सारांश सांख्यिकी तालिका डेटा के सारांशित सांख्यिकीय जानकारी का दृश्य प्रतिनिधित्व है जो तालिका रूप में प्रस्तुत किया जाता है। उदाहरण के लिए, कक्षा के 20 छात्रों के रक्त समूह O, A, B, AB, B, B, AB, O, A, B, B, AB, AB, O, O, B, A, AB, B, A हैं।
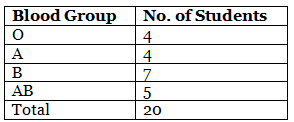
इस प्रकार, सारांश सांख्यिकी तालिका दर्शाती है कि कक्षा में 4 छात्रों का रक्त समूह O है, 4 छात्रों का रक्त समूह A है, 7 छात्रों का रक्त समूह B है और 5 छात्रों का रक्त समूह AB है। सारांश सांख्यिकी तालिका सामान्यतः जनसंख्या, बेरोजगारी, और अर्थव्यवस्था से संबंधित बड़े डेटा का प्रतिनिधित्व करने के लिए व्यवस्थित रूप से सारांशित करने के लिए उपयोग की जाती है, ताकि सटीक परिणामों की व्याख्या की जा सके।
आंकड़ों की सीमा
आंकड़ों का उपयोग कई क्षेत्रों में किया जाता है जैसे कि मनोविज्ञान, भूविज्ञान, सामाजिक विज्ञान, मौसम पूर्वानुमान, संभावना और भी बहुत कुछ। आंकड़ों का उद्देश्य डेटा से समझ प्राप्त करना है, यह अनुप्रयोगों पर ध्यान केंद्रित करता है, और इसलिए इसे एक गणितीय विज्ञान के रूप में विशिष्ट रूप से माना जाता है।
आंकड़ों में विधियाँ
विधियाँ डेटा को इकट्ठा करने, संक्षेपित करने, विश्लेषण करने और व्याख्या करने में शामिल हैं। यहां कुछ विधियाँ नीचे प्रदान की गई हैं।
- डेटा संग्रहण
- डेटा संक्षेपण
- आंकिक विश्लेषण
आंकड़ों में डेटा क्या है?
डेटा तथ्यों का एक संग्रह है, जैसे कि संख्या, शब्द, माप, अवलोकन आदि।
डेटा के प्रकार
- गुणात्मक डेटा - यह वर्णात्मक डेटा है। उदाहरण - वह तेज़ दौड़ सकती है, वह पतला है।
- संख्यात्मक डेटा - यह संख्यात्मक जानकारी है। उदाहरण - एक ऑक्टोपस आठ-पैर वाला जीव है।
संख्यात्मक डेटा के प्रकार
- अविभाज्य डेटा - इसका एक निश्चित मूल्य होता है। इसे गिना जा सकता है।
- सतत डेटा - यह निश्चित नहीं होता, बल्कि डेटा की एक श्रृंखला होती है। इसे मापा जा सकता है।
डेटा का प्रतिनिधित्व
डेटा का प्रतिनिधित्व करने के विभिन्न तरीके हैं जैसे कि ग्राफ, चार्ट या तालिकाएँ। सांख्यिकीय डेटा का सामान्य प्रतिनिधित्व इस प्रकार है:
- बार ग्राफ
- पाई चार्ट
- लाइन ग्राफ
- चित्रग्राफ
- हिस्टोग्राम
- आवृत्ति वितरण
बार ग्राफ
बार ग्राफ समूहित डेटा को आयताकार बार के साथ प्रदर्शित करता है जिनकी लंबाई उन मानों के अनुपात में होती है जिन्हें वे दर्शाते हैं। बार को लंबवत या क्षैतिज रूप से प्लॉट किया जा सकता है।
पाई चार्ट
यह एक प्रकार का ग्राफ है जिसमें एक वृत्त को क्षेत्रों में विभाजित किया जाता है। इन क्षेत्रों में से प्रत्येक पूरे का एक अनुपात दर्शाता है।
रेखा ग्राफ
रेखा चार्ट एक सीधी रेखा से जुड़े डेटा बिंदुओं की श्रृंखला द्वारा प्रदर्शित किया जाता है। डेटा बिंदुओं की श्रृंखला को 'मार्कर' कहा जाता है।
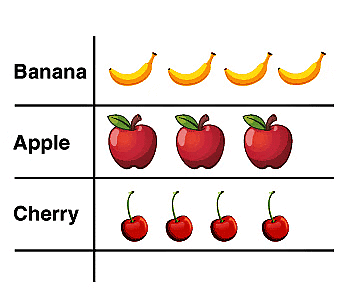
चित्रग्राफ
एक शब्द या वाक्यांश के लिए चित्रात्मक प्रतीक, अर्थात् चित्रों की मदद से डेटा दिखाना। जैसे कि सेब, केला और चेरी के अलग-अलग संख्या हो सकते हैं, और यह केवल डेटा का प्रतिनिधित्व है।
हिस्टोग्राम
एक आरेख जो आयतों से बना होता है। जिसका क्षेत्र एक चर की आवृत्ति के अनुपात में होता है और जिसकी चौड़ाई वर्ग अंतराल के बराबर होती है।
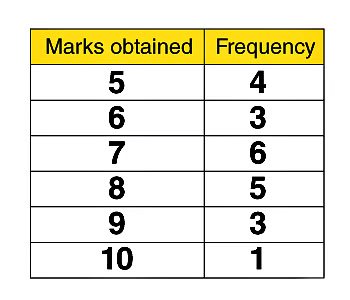
आवृत्ति वितरण
एक डेटा मान की आवृत्ति को अक्सर "f" द्वारा प्रदर्शित किया जाता है। एक आवृत्ति तालिका एकत्रित डेटा मानों को उनके संबंधित आवृत्तियों के साथ बढ़ते क्रम में व्यवस्थित करके बनाई जाती है।
केंद्रीय प्रवृत्ति के माप
गणित में, सांख्यिकी का उपयोग समूहित और असंगठित डेटा की केंद्रीय प्रवृत्तियों का वर्णन करने के लिए किया जाता है। केंद्रीय प्रवृत्ति के तीन माप हैं:
- मीन
- मेडियन
- मोड
केंद्रीय प्रवृत्ति के ये तीनों माप डेटा सेट के केंद्रीय मान को खोजने के लिए उपयोग किए जाते हैं।
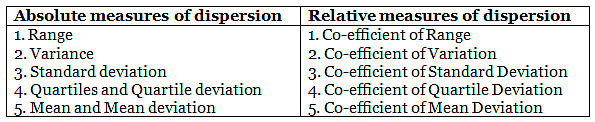
व्यतिकरण के माप
सांख्यिकी में, व्यतिकरण के माप डेटा की विविधता को समझने में मदद करते हैं, अर्थात् यह समझने में कि डेटा कितना समरूप या विषम है। सरल शब्दों में, यह दर्शाता है कि चर कितना संकुचित या बिखरा हुआ है। हालांकि, व्यतिकरण के दो प्रकार होते हैं, पूर्ण और सापेक्ष। इन्हें नीचे सारणीबद्ध किया गया है:
सांख्यिकी में स्क्यूनेस
स्क्यूनेस, सांख्यिकी में, एक संभावना वितरण में विषमत्व का माप है। यह दिए गए डेटा सेट के लिए सामान्य वितरण की वक्रता के विचलन को मापता है। स्क्यूड वितरण का मान सकारात्मक, नकारात्मक या शून्य हो सकता है। सामान्य वितरण का बेल वक्र आमतौर पर शून्य स्क्यूनेस रखता है।
ANOVA सांख्यिकी ANOVA का अर्थ है Variance का विश्लेषण। यह सांख्यिकी मॉडल का एक संग्रह है, जिसका उपयोग दिए गए डेटा सेट के लिए औसत भिन्नता को मापने के लिए किया जाता है।
स्वतंत्रता के डिग्री
सांख्यिकीय विश्लेषण में, स्वतंत्रता के डिग्री का उपयोग उन मूल्यों के लिए किया जाता है जो बदलने के लिए स्वतंत्र होते हैं। स्वतंत्र डेटा या जानकारी, जिसे एक पैरामीटर का अनुमान लगाने के दौरान स्थानांतरित किया जा सकता है, वह स्वतंत्रता के डिग्री कहलाता है।
सांख्यिकी के अनुप्रयोग
सांख्यिकी के गणित और वास्तविक जीवन में व्यापक अनुप्रयोग हैं। सांख्यिकी के कुछ अनुप्रयोग निम्नलिखित हैं:
- अनुप्रयुक्त सांख्यिकी, सैद्धांतिक सांख्यिकी और गणितीय सांख्यिकी
- मशीन लर्निंग और डेटा माइनिंग
- समाज में सांख्यिकी
- सांख्यिकीय कम्प्यूटिंग
- कला के गणित पर लागू सांख्यिकी
संभाव्यता के शर्तें और परिभाषाएँ
- नमूना बिंदु: यह संभावित परिणामों में से एक को दर्शाता है। उदाहरण के लिए, एक ताश के पत्तों के डेक में ♥4 एक नमूना बिंदु है, इसी तरह, ♣क्वीन भी एक नमूना बिंदु है।
- प्रयोग या परीक्षण: परीक्षणों की एक श्रृंखला जहां परिणाम हमेशा अप्रत्याशित होते हैं। उदाहरण के लिए, सिक्का उछालना, ताश के पत्तों में से एक कार्ड चुनना, डाइस फेंकना, आदि।
- नमूना स्थान: सभी संभावित परिणामों का सेट नमूना स्थान कहलाता है, इसे S द्वारा दर्शाया जाता है।
- अनुकूल परिणाम: अनुकूल परिणाम, जैसा कि नाम से स्पष्ट है, वे परिणाम हैं जिनमें एक व्यक्ति रुचि रखता है।
- समान संभावित घटनाएँ: किसी भी घटनाओं के सेट को समान संभावित कहा जाता है यदि उनके घटित होने की संभावना समान हो। उदाहरण के लिए: जब डाइस फेंका जाता है, तो छह (1 से 6 तक के घटनाएँ) समान संभावित होती हैं।
- व्यापक घटनाएँ: घटनाओं के एक सेट को व्यापक कहा जाता है यदि उनमें से कम से कम एक घटना हमेशा प्रयोग के निष्पादन के दौरान होती है। उदाहरण के लिए, सिक्का उछालने का उदाहरण लेते हैं, यहाँ 1 से 6 तक सभी घटनाएँ व्यापक हैं।
- आपसी विशेष घटनाएँ: घटनाओं के एक सेट को आपसी विशेष कहा जाता है यदि उनमें से किसी एक घटना का घटित होना किसी अन्य घटना के घटित होने की संभावना को रोकता है। आपसी विशेष घटनाएँ समान नमूना स्थान में होती हैं। यदि A और B दोनों समान नमूना स्थान में आपसी विशेष घटनाएँ हैं, तो P(A∩B) = 0।
- स्वतंत्र घटनाएँ: घटनाओं के एक सेट को स्वतंत्र कहा जाता है यदि किसी घटना का घटित होना अन्य घटनाओं के घटित होने से प्रभावित नहीं होता। स्वतंत्र घटनाएँ विभिन्न नमूना स्थानों में होती हैं। यदि A और B दोनों विभिन्न नमूना स्थानों में स्वतंत्र घटनाएँ हैं, तो P(A∩B) = P(A)P(B)।
- निर्भर घटनाएँ: यदि एक घटना का घटित होना दूसरी घटना की संभावना को प्रभावित करता है, तो ये दोनों घटनाएँ निर्भर कहलाती हैं। अब जब हम संभाव्यता की परिभाषाएँ और शर्तें जान चुके हैं, तो चलिए संभाव्यता के सिद्धांत, इसकी परिभाषा और अन्य संबंधित अवधारणाओं की ओर बढ़ते हैं।
- पूरक घटना: इस प्रकार की घटना घटनाओं के न होने को दर्शाती है। किसी घटना P का पूरक घटना, न P (या P’) है।
- असंभव घटना: वह घटना जो नहीं हो सकती, उसे असंभव घटना कहा जाता है। उदाहरण के लिए, सिक्का उछालने में एक ही समय में सिर और पूंछ आना असंभव है।
संभाव्यता की परिभाषा किसी घटना की संभाव्यता की गणितीय परिभाषा इसकी अनुकूल मामलों की संख्या का कुल मामलों की संख्या के अनुपात के रूप में परिभाषित की जाती है। S को एक नमूना स्थान मानते हैं और E को एक घटना मानते हैं, ऐसा मानते हैं कि n(S) = n, n(E) = m और प्रत्येक परिणाम समान रूप से संभावित है। तब
संभावनाओं के प्रकार
संभावनाओं की तीन महत्वपूर्ण श्रेणियाँ हैं:
- सैद्धांतिक संभावना
- प्रायोगिक संभावना
- आक्ष्मिक संभावना
आइए हम इन तीनों के बारे में विस्तार से जानते हैं:
सैद्धांतिक संभावना
सैद्धांतिक संभावना किसी घटना के घटने की संभावनाओं पर आधारित होती है। यह संभावना मुख्यतः संभाव्यता के पीछे के तर्क पर निर्भर करती है। उदाहरण के लिए, यदि एक सिक्का उछाला जाता है, तो सिर या पूँछ आने की सैद्धांतिक संभावना ½ या 0.5 होगी।
प्रायोगिक संभावना
यह प्रकार की संभावना एक प्रयोग के अवलोकनों पर आधारित होती है। प्रायोगिक संभावना को संभावित परिणामों की संख्या को कुल परीक्षणों की संख्या से निर्धारित किया जा सकता है। उदाहरण के लिए, यदि एक सिक्का 8 बार उछाला जाता है और सिर 4 बार आता है, तो सिर आने की प्रायोगिक संभावना 4/8 या 1/2 होगी।
आक्ष्मिक संभावना
आक्ष्मिक संभावना में एक सेट कमांड या धारणाएँ निर्धारित की जाती हैं जो सभी प्रकारों पर लागू होती हैं। ये आक्सिमों को कोलमोरोव द्वारा सेट किया गया है और इन्हें कोलमोरोव के तीन आक्सिम कहते हैं। आक्ष्मिक संभावना के तरीकों से घटनाओं के अस्तित्व या अनुपस्थिति की संभावनाओं को मापना संभव है।
पूरक घटनाएँ
ऐसी घटनाएँ जिनमें केवल दो परिणाम हो सकते हैं, जो यह बताती हैं कि कोई घटना होगी या नहीं होगी। उदाहरण के लिए, एक व्यक्ति आपके निवास पर आएगा या नहीं आएगा, सरकारी नौकरी पाना या नौकरी न पाना आदि पूरक घटनाओं के उदाहरण हैं। किसी घटना के घटने की पूरक संभावना, उस घटना के न घटने की संभावना का बिल्कुल विपरीत होती है। कुछ और अतिरिक्त उदाहरण हैं:

संभाव्यता घनत्व फ़ंक्शन
संभाव्यता घनत्व फ़ंक्शन (PDF) वह संभाव्यता फ़ंक्शन है जो एक निरंतर यादृच्छिक चर की घनत्व के लिए निर्धारित किया गया है, जो निश्चित मानों की श्रेणी में विद्यमान है। PDF सामान्य वितरण को स्पष्ट करता है और यह बताता है कि कैसे औसत और विचलन मौजूद हैं। मानक सामान्य वितरण का उपयोग सांख्यिकी के एक डेटाबेस को बनाने के लिए किया जाता है, जो अक्सर विज्ञान में वास्तविक मान वाले चर का वर्णन करने के लिए उपयोग किया जाता है, जिसका वितरण पहचाना नहीं गया है।
संभाव्यता के सूत्र
संभाव्यता के उदाहरणों में, एक चीज जो बहुत मदद करती है, वह है सूत्र और प्रमेय, क्योंकि कभी-कभी संभाव्यता थोड़ी भ्रमित करने वाली हो जाती है, इसलिए हम अगले भाग में सूत्रों पर नज़र डालेंगे;
- P(A ∪ B) = P(A) P(B) – P(A ∩ B).
- यदि A और B पारस्परिक रूप से विशेष घटनाएँ हैं, अर्थात् A ∩ B = ϕ, तो P(A ∪ B) = P(A) P(B).
- यदि A, B, और C कोई तीन घटनाएँ हैं, तो जोड़ने का सूत्र इस प्रकार है; P(A ∪ B ∪ C) = P(A) P(B) P(C) – P(A ∩ B) – P(B ∩ C) – P(A ∩ C) + P(A ∩ B ∩ C)
- यदि A, B, और C कोई तीन घटनाएँ हैं जो पारस्परिक रूप से विशेष हैं, तो; P(A ∪ B ∪ C) = P(A) P(B) P(C)
संविधानिक संभाव्यता
मान लें A और B कोई दो घटनाएँ हैं जो एक यादृच्छिक प्रयोग से संबंधित हैं। फिर, घटना A की होने की संभाव्यता उस स्थिति में, जब B पहले ही हो चुकी है, और B की संभाव्यता शून्य के बराबर नहीं है (P(B) ≠ 0), इसे संविधानिक संभाव्यता कहा जाता है और इसे P(A|B) द्वारा दर्शाया जाता है।
संभावना के सशर्त बिंदु
- यदि E घटना का पूरक है, तो किसी भी घटना A के लिए, 0 ≤ P(A) ≤ 1, यह संभावना का दायरा है।
- यदि A और B स्वतंत्र घटनाएँ हैं, तो P(B|A) = P(B) ∵ P(A∩B) = P(A)×P(B)
संभावना के लिए याद रखने योग्य बिंदु
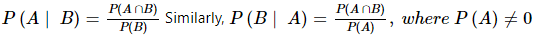
यदि A और B किसी यादृच्छिक प्रयोग में दो घटनाएँ हैं, तो; P(A ∩ B) = P(A | B) P(B), यदि P(B) ≠ 0। P(A ∩ B) = P(B | A) P(A), यदि P(A) ≠ 0।
महत्वपूर्ण संभावना प्रमेय और वितरण
इस अनुभाग में हम कुछ महत्वपूर्ण संभावना संबंधित प्रमेयों की जांच करेंगे जैसे कुल संभावना का नियम, बायेस का प्रमेय, बाइनोमियल वितरण आदि।
कुल संभावना का नियम: मान लीजिए E1, E2, ….., En n आपस में विशिष्ट और पूर्ण घटनाएँ हैं जो एक यादृच्छिक प्रयोग से संबंधित हैं। यदि A एक घटना है जो E1 या E2 या ... या En के साथ होती है, तो; P(A) = P(E1) × P(A | E1) + P(E2) × P(A | E2) + ... + P(En) × P(A | En)।
बायेस का प्रमेय: मान लीजिए E1, E2, ….., En n आपस में विशिष्ट और पूर्ण घटनाएँ हैं जो एक यादृच्छिक प्रयोग से संबंधित हैं और S नमूना स्थान है। यदि A एक घटना है जो E1 या E2 या ... या En के साथ होती है, ऐसी स्थिति में P(A) ≠ 0।
बाइनोमियल वितरण: यदि किसी घटना में विशेष प्रयास की सफलता की संभावना p है और असफलता की संभावना q = 1 – p है, तो n स्वतंत्र प्रयोगों में ठीक x सफल घटनाओं की संभावना इस प्रकार है:
बाइनोमियल वितरण का औसत और विचलन: बाइनोमियल वितरण B(n, p) का औसत और विचलन इस प्रकार दिया गया है:
औसत: औसत, माध्य, और मोड का कुछ सिद्धांत: औसत को औसत मान/अपेक्षित मान के रूप में परिभाषित किया गया है। माध्य डेटा/अवलोकन की केंद्रीय भाग है। मोड उस भाग से संबंधित है जो प्रदान किए गए अवलोकन में सबसे अधिक हुआ है। औसत, माध्य, और मोड के बीच का संबंध इस प्रकार है; मोड = 3 माध्य – 2 औसत।
संभावना के हल किए गए समस्याएँ
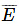
हल की गई संभावना के उदाहरणों के साथ संभावना के बारे में अधिक जानें:
उदाहरण 1: दो पासे एक साथ फेंके जाते हैं। उनके ऊपर आए संख्याओं का कुल योग एक प्रमुख संख्या है, इसकी संभावना ज्ञात कीजिए।
हल: दो पासों को एक साथ फेंकने के लिए नमूना स्थान है: S = {(a, b)} {जहाँ a = 1, 2, ….., 6 और b = 1, 2, ……, 6} ⇒ n (S) = 36
मान लीजिए A S का एक उपसमुच्चय है जिसे इस प्रकार परिभाषित किया गया है: A = {(a, b) | a+b एक प्रमुख संख्या है}। A = {(1, 1), (1, 2), (1, 4), (1, 6), (2, 1), (2, 3), (2, 5), (3, 2), (3, 4), (4, 1), (4, 3), (5, 2), (5, 6), (6, 1), (6, 5)} ⇒ n (A) = 15।
उदाहरण 2: यदि एक निष्पक्ष पासा 4 बार फेंका जाता है, तो ठीक 2 बार 6 आने की संभावना ज्ञात कीजिए।
हल: दिया गया, एक निष्पक्ष पासा 4 बार फेंका जाता है। मान लीजिए p 6 आने की संभावना है = 1 / 6 और q 6 न आने की संभावना है, अर्थात = 1 – (1 / 6) = 5 / 6
जैसा कि हम जानते हैं, बाइनोमियल वितरण के अनुसार: यहाँ हम पाते हैं, n = 4, x = 2, p = 1 / 6 और q = 5 / 6।
इसलिए निष्पक्ष पासा 4 बार फेंके जाने पर ठीक 2 बार 6 आने की संभावना इस प्रकार है;
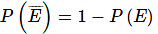
मान लीजिए कि E1, E2, ….., En एक बेतरतीब प्रयोग से जुड़े n पारस्परिक रूप से विशिष्ट और समग्र घटनाएँ हैं। यदि A एक ऐसी घटना है जो E1 या E2 या … या En के साथ होती है, तो:
P(A) = P(E1) × P(A | E1) + P(E2) × P(A | E2) + … + P(En) × P(A | En)
संभाव्यता के बारे में अधिक जानें, हल की गई संभाव्यता उदाहरणों के साथ:
उदाहरण 1: दो पासे एक साथ फेंके जाते हैं। उन पर आने वाले संख्याओं का योग एक अभाज्य संख्या (prime number) होने की संभावना ज्ञात कीजिए।
समाधान: दो पासों के एक साथ फेंकने के लिए नमूना स्थान है: S = {(a, b)} {जहाँ a = 1, 2, ….., 6 और b = 1, 2, ……, 6} ⇒ n (S) = 36
मान लीजिए A एक उपसमुच्चय है S का, जिसे इस प्रकार परिभाषित किया गया है:
A = {(a, b) | a + b एक अभाज्य संख्या है। A = {(1, 1), (1, 2), (1, 4), (1, 6), (2, 1), (2, 3), (2, 5), (3, 2), (3, 4), (4, 1), (4, 3), (5, 2), (5, 6), (6, 1), (6, 5)} ⇒ n (A) = 15
जैसा कि हम जानते हैं:
उदाहरण 2: यदि एक निष्पक्ष पासा 4 बार फेंका जाता है, तो ठीक 2 बार 6 आने की संभावना ज्ञात कीजिए।
समाधान: दिया गया है, एक निष्पक्ष पासा 4 बार फेंका जाता है। मान लीजिए p 6 आने की संभावना है = 1 / 6 और q 6 न आने की संभावना है, यानी = 1 – (1 / 6) = 5 / 6
जैसा कि हम जानते हैं, बायनॉमियल वितरण के अनुसार: यहाँ हम पाते हैं, n = 4, x = 2, p = 1 / 6 और q = 5 / 6। अतः जब एक निष्पक्ष पासा 4 बार फेंका जाता है, तो ठीक 2 बार 6 आने की संभावना इस प्रकार दी जाती है:
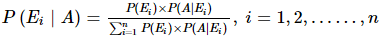
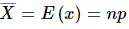
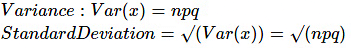
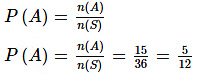
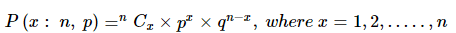
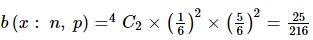
|
142 videos|172 docs|185 tests
|















