सूत्र: संभावना | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download
संभावना के लिए सूत्र और परिभाषा
- संभावना एक संख्यात्मक प्रतिनिधित्व है जो किसी विशेष घटना के होने की संभावना या संभावना को दर्शाता है।
- संभावना यह दर्शाती है कि घटनाएँ कितनी बार होती हैं। जब घटनाएँ होती हैं, जैसे कि गेंद फेंकना या किसी पत्ते को चुनना, तो प्रत्येक घटना के साथ एक संबंधित संभावना होती है।
- गणितीय दृष्टिकोण से, संभावना को अनुकूल परिणामों की संख्या और संभावित परिणामों की कुल संख्या के अनुपात के रूप में परिभाषित किया जाता है।
- संभावना का सिद्धांत तीन दृष्टिकोणों को शामिल करता है: क्लासिकल अप्रोच, रिलेटिव फ्रिक्वेंसी अप्रोच, और सब्जेक्टिव अप्रोच।
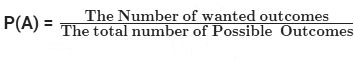

मूल परिभाषा और सूत्र
- यादृच्छिक घटना: यदि किसी प्रयोग को समान परिस्थितियों में कई बार दोहराया जाता है और प्रत्येक बार वही परिणाम नहीं मिलता, लेकिन एक परीक्षण में परिणाम कई संभावित परिणामों में से एक होता है, तो ऐसे प्रयोग को यादृच्छिक घटना या संभाव्य घटना कहा जाता है।
- मूल घटना: मूल घटना यादृच्छिक घटना की प्रत्येक घटना का परिणाम दर्शाती है। जब भी यादृच्छिक घटना होती है, तो प्रत्येक संबंधित परिणाम को मूल घटना के रूप में संदर्भित किया जाता है।
- नमूना स्थान: नमूना स्थान यादृच्छिक घटना के सभी संभावित परिणामों के सेट को दर्शाता है। उदाहरण के लिए, जब एक सिक्का उछाला जाता है, तो संभावित परिणाम सिर और पूंछ होते हैं।
- घटना: एक घटना उस नमूना स्थान का उपसमुच्चय है जो एक यादृच्छिक घटना से संबंधित है।
- घटना का घटित होना: एक यादृच्छिक घटना से संबंधित घटना को तब घटित माना जाता है जब इसके भीतर कोई भी मूल घटना वास्तविक परिणाम है।
मूल संभावना सूत्र
मूल संभावना सूत्र
- संभावना सीमा – 0 ≤ P(A) ≤ 1
- पूरक घटनाओं का नियम – P(AC) + P(A) = 1
- योग का नियम – P(A∪B) = P(A) + P(B) – P(A∩B)
- विभाज्य घटनाएँ – घटनाएँ A और B विभाज्य हैं यदि P(A∩B) = 0
- सशर्त संभावना – बेयेस सूत्र
- स्वतंत्र घटनाएँ – घटनाएँ A और B स्वतंत्र हैं यदि P(A∩B) = P(A) ⋅ P(B)
नमूना संभावना आधारित प्रश्न
प्रश्न 1: एक बैग में 7 लाल गोले, 5 नीले गोले, और 4 हरे गोले हैं। बैग से बिना प्रतिस्थापन के दो गोले यादृच्छिक रूप से चुने जाते हैं। दोनों नीले होने की संभावना क्या है?
हल: पहले खींचने पर, नीले गोले को चुनने की संभावना 5/16 है (16 कुल गोले में से 5 नीले गोले)। पहले गोले के खींचने के बाद, 15 कुल गोले में से 4 नीले गोले बचे हैं। दूसरे खींचने पर, नीले गोले को चुनने की संभावना 4/15 है। दोनों गोले नीले होने की संभावना की गणना करने के लिए => संभावना = 20/24 = 5/6
प्रश्न 2: एक बैग में 3 हरे बल्ब, 4 नारंगी बल्ब और 5 सफेद बल्ब हैं। बैग से एक बल्ब यादृच्छिक रूप से उठाया जाता है। हरे या सफेद बल्ब को चुनने की संभावना क्या है?
हल: बैग में बल्बों की कुल संख्या 3 हरे + 4 नारंगी + 5 सफेद = 12 बल्ब हैं। हरे बल्बों की संख्या 3 है, और सफेद बल्बों की संख्या 5 है। हरे या सफेद बल्ब चुनने की संभावना, हम हरे बल्बों और सफेद बल्बों की संख्या को जोड़ते हैं, और फिर इसे बल्बों की कुल संख्या से विभाजित करते हैं। संभावना = (हरे बल्बों की संख्या + सफेद बल्बों की संख्या) / बल्बों की कुल संख्या = 8/12 = 2/3
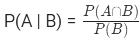
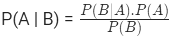
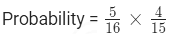
प्रश्न 3: जोई ट्रिबियानी ने दो प्रतिभागियों के साथ एक रैक रेस आयोजित की। पहले प्रतिभागी के जीतने की संभावना 2/7 है, और दूसरे प्रतिभागी के जीतने की संभावना 3/5 है। उनकी में से एक के जीतने की संभावना क्या है? हल: मान लेते हैं:
P(A) = पहले प्रतिभागी के जीतने की संभावना = 2/7
P(B) = दूसरे प्रतिभागी के जीतने की संभावना = 3/5
दोनों प्रतिभागियों के एक साथ जीतने की संभावना (टाई) शून्य है क्योंकि केवल एक विजेता हो सकता है। इसलिए, उनमें से एक के जीतने की संभावना है:
P(उनमें से एक जीतता है) = P(A) + P(B) – P(A और B)
P(उनमें से एक जीतता है) = P(A) + P(B) – 0 (क्योंकि P(A और B) = 0)
P(उनमें से एक जीतता है) = P(A) + P(B)
दिए गए संभावनाओं को प्रतिस्थापित करते हुए:
प्रश्न 4: एक दराज में 4 काले पेन, 3 नीले पेन, और 5 लाल पेन हैं। दराज से एक पेन यादृच्छिक रूप से निकाली जाती है। यह काला या नीला होने की संभावना क्या है? हल: हमें दराज से एक काले या नीले पेन निकालने की संभावना की गणना करनी है।
दराज में कुल पेन की संख्या है: 4 काले + 3 नीले + 5 लाल = 12 पेन
काले पेन निकालने की संभावना है 4/12
नीले पेन निकालने की संभावना है 3/12 = 1/4
इसलिए, काले या नीले पेन निकालने की संभावना को हम व्यक्तिगत संभावनाओं को जोड़कर प्राप्त करते हैं:
संभावना = 4/12 + 3/12
संभावना = 7/12
प्रश्न 5: सिल्वेस्टर स्टेलोन ने छात्रों के एक समूह के लिए गुब्बारों का एक डिब्बा लाया। डिब्बे में 3 आकार A के गुब्बारे, 4 आकार B के गुब्बारे, और 5 आकार C के गुब्बारे हैं। यदि डिब्बे से तीन गुब्बारे यादृच्छिक रूप से निकाले जाते हैं, तो सभी तीन गुब्बारे विभिन्न आकारों के होने की संभावना क्या है? हल: गुब्बारों की कुल संख्या = 3 आकार A के गुब्बारे + 4 आकार B के गुब्बारे + 5 आकार C के गुब्बारे = 12
n(s) = 12C3 = 220
n(e) = 3C1 * 4C1 * 5C1 = 60
P = 60/220 = 3/11

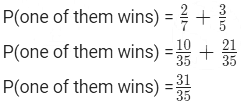
|
142 videos|172 docs|185 tests
|
















