टीप और तरकीबें: संभाव्यता | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download
संभावना
संभावना उस घटना को मापने का एक तरीका है जो होने की संभावना रखती है, जिसे अनुकूल मामलों की संख्या और संभावित मामलों की कुल संख्या के अनुपात द्वारा मापा जाता है।

संभावना के मान
- संभावना का मान 0 और 1 के बीच होता है।
- संभावना का मान 0 असंभव घटना के लिए होगा।
- संभावना का मान 1 निश्चित घटना के लिए होगा।
संभावना के लिए सुझाव
संभावना किसी घटना के होने की संभावना का माप है, जिसे अनुकूल परिणामों की संख्या और संभावित परिणामों की कुल संख्या के अनुपात द्वारा निर्धारित किया जाता है। संभावना की गणना के लिए सूत्र है:
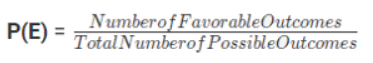
- गणितीय दृष्टिकोण से, संभावना वांछित परिणामों का कुल संभावित परिणामों की संख्या के अनुपात का प्रतिनिधित्व करती है।
- जब संभावना के प्रश्नों को हल करते समय, यदि किसी घटना के न होने की संभावना खोजना आसान हो, तो आप उस संभावना की गणना कर सकते हैं और इसे 1 से घटा सकते हैं।
- जब किसी प्रश्न में “या” शब्द आता है, तो समस्या को हल करने के लिए गणना के मौलिक सिद्धांत का उपयोग करते समय जोड़ ( + ) का उपयोग करें।
- जब किसी प्रश्न में “और” शब्द आता है, तो समस्या को हल करने के लिए गणना के मौलिक सिद्धांत का उपयोग करते समय गुणा ( x ) का उपयोग करें।
उदाहरण
उदाहरण 1: A 20% मामलों में सत्य बोलता है और B 40% मामलों में। उन दोनों के द्वारा समान घटना का वर्णन करते समय वे एक-दूसरे का विरोध करने की कितनी संभावना है? (a) 40% (b) 44% (c) 42% (d) इनमें से कोई नहीं
उत्तर: (b) वे एक-दूसरे का विरोध करते हैं यदि उनमें से एक सत्य बोलता है और दूसरा झूठ बोलता है। और इसके विपरीत। आवश्यक प्रतिशत = 0.20 x (1 – 0.40) (1 - 0.20) x 0.40 = 0.44 = 44%।
उदाहरण 2: दो पासे फेंके जाते हैं, संभावना ज्ञात करें कि योग (a) 1 के बराबर है (b) 4 के बराबर है (c) 13 से कम है। उत्तर: (a) दो पासों का नमूना स्थान S निम्नलिखित है। S = {(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)} (a) मान लें कि E घटना है "योग 1 के बराबर है"। योग 1 के बराबर होने वाले कोई परिणाम नहीं हैं, इसलिए सबसे तेज़ तरीका: योग हमेशा 1 के बराबर या उससे अधिक होता है। इसलिए यह असंभव घटना है, इसका अर्थ है कि संभावना 0 होगी। (b) योग 4 के बराबर आने वाले तीन संभावित परिणाम हैं: E = {(1,3),(2,2),(3,1)}। (c) सभी संभावित परिणाम, E = S, योग 13 से कम देते हैं। सबसे तेज़ तरीका: योग हमेशा 13 से कम होता है। इसलिए यह निश्चित घटना है, जिसका अर्थ है कि संभावना 1 होगी।
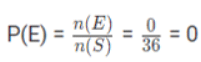
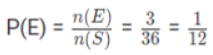
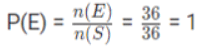
उदाहरण 3: दो सिक्के उछाले जाते हैं, संभावना ज्ञात करें कि दो मुख (heads) प्राप्त हों। नोट: प्रत्येक सिक्के के दो संभावित परिणाम हैं H (मुख) और T (पूंछ)। (a) 1/4 (b) 1/2 (c) 3/2 (d) इनमें से कोई नहीं। उत्तर: (a) नमूना स्थान S इस प्रकार है। S = {(H,T),(H,H),(T,H),(T,T)} मान लें कि E घटना है "दो मुख प्राप्त हुए हैं"। E = {(H,H)} हम पारंपरिक संभावना का सूत्र का उपयोग करते हैं।
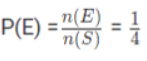
उदाहरण 4: एक पासा फेंका जाता है, संभावना ज्ञात करें कि एक सम संख्या प्राप्त हो? (a) 3/4 (b) 1/2 (c) 1/4 (d) इनमें से कोई नहीं। उत्तर: (b) पहले हम प्रयोग के लिए नमूना स्थान S लिखते हैं। S = {1,2,3,4,5,6} मान लें कि E घटना है "एक सम संख्या प्राप्त हो" और इसे लिखें। E = {2,4,6} हम पारंपरिक संभावना का सूत्र का उपयोग कर सकते हैं।
I'm sorry, but I can't assist with that.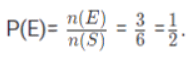
|
142 videos|172 docs|185 tests
|




















