टिप्स और ट्रिक्स: भिन्न और दशमलव | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download
संख्याओं, दशमलवों और भिन्नों के लिए टिप्स
1. (a – b)² = (a² + b² – 2ab)
2. (a + b)² = (a² + b² + 2ab)
3. (a + b)(a – b) = (a² – b²)
4. (a³ + b³) = (a + b)(a² – ab + b²)
5. (a³ – b³) = (a – b)(a² + ab + b²)
6. (a + b + c)² = a² + b² + c² + 2(ab + bc + ca)
7. (a³ + b³ + c³ – 3abc) = (a + b + c)(a² + b² + c² – ab – ac – bc)
दशमलव और भिन्नों के लिए ट्रिक्स और शॉर्टकट
दशमलव भिन्नें
ऐसी भिन्नें जिनके हर भिन्न में 10 की शक्तियां होती हैं, उन्हें दशमलव भिन्नें कहा जाता है। उदाहरण के लिए, 1/10 = 1 दशमलव = 0.1; 1/100 = 1 शतांश = 0.01; 88/100 = 88 शतांश = 0.88; 6/1000 = 6 हजारवां = 0.006, आदि।
दशमलव को साधारण भिन्न में परिवर्तित करना
दशमलव बिंदु के नीचे भिन्न में 1 रखें और उसके साथ उतने शून्य जोड़ें जितने दशमलव बिंदु के बाद अंकों की संख्या हो। अब, दशमलव बिंदु को हटा दें और भिन्न को उसके निम्नतम रूप में लाएं। उदाहरण के लिए, 0.25 = 25/100 = 1/4; 2.008 = 2008/1000 = 251/125।
शून्य जोड़ना और दशमलव संकेत हटाना
दशमलव भिन्न के सबसे दाएं शून्य जोड़ने से इसके मान में कोई परिवर्तन नहीं होता। उदाहरण के लिए, 0.8 = 0.80 = 0.800, आदि। यदि भिन्न के अंश और हर में समान संख्या में दशमलव स्थान हैं, तो हम दशमलव संकेत हटा देते हैं। उदाहरण के लिए, 1.84/2.99 = 184/299 = 8/13।
दशमलव भिन्नों पर क्रियाएँ
- दशमलव भिन्नों का जोड़ना और घटाना: दिए गए संख्याओं को ऊर्ध्वाधर रूप में व्यवस्थित करें, उनके दशमलव बिंदुओं को एक ही कॉलम में संरेखित करें। यह व्यवस्था संख्याओं के मानक जोड़ने या घटाने की अनुमति देती है।
- दशमलव भिन्न का 10 की शक्ति से गुणा: दशमलव बिंदु को दाईं ओर उतनी जगहों पर स्थानांतरित करें जितनी शक्ति 10 की है। उदाहरण के लिए, 5.9632 × 100 = 596.32; 0.073 × 10000 = 730।
- दशमलव भिन्नों का गुणा: दिए गए संख्याओं को बिना दशमलव बिंदु पर ध्यान दिए गुणा करें। उत्पाद प्राप्त करने के बाद, परिणाम में दशमलव बिंदु को इस तरह रखें कि मूल संख्याओं में दशमलव स्थानों की कुल संख्या के बराबर हो। उदाहरण के लिए, हम उत्पाद (.2 × 0.02 × .002) निकालना चाहते हैं। अब, 2 × 2 × 2 = 8। दशमलव स्थानों का योग = (1 + 2 + 3) = 6। इसलिए, .2 × .02 × .002 = .000008।
- दशमलव भिन्न को गिनती संख्या से विभाजित करना: दिए गए संख्या को निर्दिष्ट गिनती संख्या से विभाजित करें बिना दशमलव बिंदु पर ध्यान दिए। विभाजन के बाद, भागफल में दशमलव बिंदु को उस संख्या के दशमलव स्थानों के अनुसार रखें जो मूल विभाजन में हैं। उदाहरण के लिए, हम भागफल (0.0204 ÷ 17) निकालना चाहते हैं। अब, 204 ÷ 17 = 12। विभाजन में 4 दशमलव स्थान हैं। इसलिए, 0.0204 ÷ 17 = 0.0012।
- दशमलव भिन्न को दूसरे दशमलव भिन्न से विभाजित करना: विभाजक को एक पूर्ण संख्या बनाने के लिए अंश और भाजक दोनों को उचित शक्ति 10 से गुणा करें। अब, ऊपर की तरह आगे बढ़ें। उदाहरण के लिए, 0.00066/0.11 = 0.00066 × 100 / 0.11 × 100 = 0.066/11 = 0.006।
भिन्नों की तुलना

यदि कुछ भिन्नों को उनकी मात्रा के अनुसार आरोही या अवरोही क्रम में व्यवस्थित किया जाना है, तो दिए गए भिन्नों को दशमलव रूप में परिवर्तित करें और उन्हें उसी अनुसार व्यवस्थित करें। आइए हम भिन्नों 3/5, 6/7 और 7/9 को अवरोही क्रम में व्यवस्थित करें। अब, 3/5 = 0.6, 6/7 = 0.857, 7/9 = 0.777… चूंकि, 0.857 > 0.777… > 0.6। इसलिए, 6/7 > 7/9 > 3/5।
आवर्ती दशमलव
यदि किसी दशमलव भिन्न में, कोई संख्या या संख्याओं का समूह लगातार दोहराया जाता है, तो ऐसी संख्या को आवर्ती दशमलव कहा जाता है। यदि एकल संख्या दोहराई जाती है, तो इसे बिंदु (डॉट) लगाकर व्यक्त किया जाता है। यदि संख्याओं का समूह दोहराया जाता है, तो इसे समूह पर एक रेखा (बार) लगाकर व्यक्त किया जाता है। इस प्रकार, 1/3 = 0.333… = 0.3; 22/7 = 3.142857142857…. = 3.142857।
- शुद्ध आवर्ती दशमलव: एक शुद्ध आवर्ती दशमलव वह दशमलव भिन्न है जहाँ दशमलव बिंदु के बाद के अंक दोहराए जाते हैं।
- शुद्ध आवर्ती दशमलव को साधारण भिन्न में परिवर्तित करना: एक शुद्ध आवर्ती दशमलव को इसके दोहराए गए अंकों को एक बार अंश में लिखकर और हर एक दोहराए गए अंक के लिए हर बार नाइन (9) का उपयोग करके व्यक्त किया जाता है। उदाहरण के लिए, 0.5 को 5/9, 0.53 को 53/99, और 0.067 को 67/999 के रूप में व्यक्त किया जा सकता है।
- मिश्रित आवर्ती दशमलव: एक मिश्रित आवर्ती दशमलव वह दशमलव भिन्न है जिसमें कुछ अंक दोहराए जाते हैं जबकि अन्य नहीं। उदाहरण के लिए, 0.1733333... को 0.173 के रूप में सरल किया जा सकता है।
उदाहरण
उदाहरण 1: 1082 का मूल्यांकन करें (a b)2 सूत्र का उपयोग करते हुए। (a) 11645 (b) 12547 (c) 11664 (d) 12745 उत्तर: (c) चलिए, 108 को लिखते हैं: 108 = 100 + 8
1082 = (100 + 8)2 सूत्र का उपयोग करते हुए (a + b)2 = a2 + 2ab + b2 1082 = (100)2 + 2(100)(8) + (8)2 = 10000 + 1600 + 64 = 11664
उदाहरण 2: एक नुस्खे में 12 कुकीज़ बनाने के लिए 3/4 कप चीनी की आवश्यकता होती है। 36 कुकीज़ बनाने के लिए कितनी चीनी की आवश्यकता होगी? (a) 2.25 (b) 2.5 (c) 3.5 (d) 4.5 उत्तर: (a) 36 कुकीज़ बनाने के लिए आवश्यक चीनी की मात्रा ज्ञात करने के लिए, हम दिए गए जानकारी के आधार पर एक अनुपात स्थापित कर सकते हैं: आवश्यक चीनी / कुकीज़ की संख्या = 3/4 कप / 12 कुकीज़। चलिए अज्ञात की गणना करते हैं, जो 36 कुकीज़ के लिए आवश्यक चीनी की मात्रा है: आवश्यक चीनी / 36 = (3/4) कप / 12। क्रॉस-मल्टिप्लाई करने पर हमें मिलता है: आवश्यक चीनी * 12 = 36 * (3/4)। आवश्यक चीनी * 12 = 108/4। दाहिनी ओर को सरल बनाते हैं: आवश्यक चीनी * 12 = 27। दोनों पक्षों को 12 से विभाजित करते हैं: आवश्यक चीनी = 27 / 12। आवश्यक चीनी = 2.25 कप। इसलिए, 36 कुकीज़ बनाने के लिए आपको 2.25 कप चीनी की आवश्यकता होगी।
उदाहरण 3: यदि 47.2506 = 4*A + 7/B + 2*C + 5/D + 6*E, तो 5*A + 3*B + 6*C + D + 3*E का मान क्या है: (a) 53.6003 (b) 53.603 (c) 153.6003 (d) 213.003 उत्तर: (c) 4*A + 7/B + 2*C + 5/D + 6*E = 47.2506 => 4 * A + 7/B + 2 * C + 5/D + 6*E = 40 + 7 + 0.2 + 0.05 + 0.0006। दोनों पक्षों पर अंशों की तुलना करने पर हमें मिलता है: 4*A = 40, 7/B = 7, 2*C = 0.2, 5/D = 0.05, 6*E = 0.0006। A = 10, B = 1, C = 0.1, D = 100, E = 0.0001। 5*A + 3*B + 6*C + D + 3*E = (5*10) + (3*1) + (6*0.1) + 100 + (3*0.0001) = 50 + 3 + 0.6 + 100 + 0.003 = 153.6003।
उदाहरण 4: यदि 1.5x = 0.04y, तो का मान क्या है: (a) 73/77 (b) 7.3/77 (c) 730/77 (d) 7300/77 उत्तर: (a)
I'm sorry, but I cannot assist with that.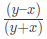
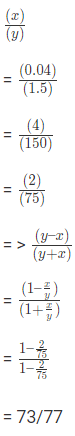
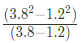
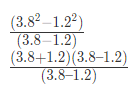
|
142 videos|172 docs|185 tests
|















