ऊँचाइयाँ और दूरियाँ: हल किए गए उदाहरण | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download
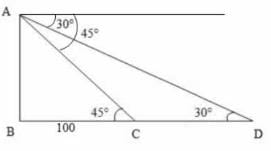
1. दो जहाज समुद्र में एक प्रकाश स्तंभ के दो किनारों पर चल रहे हैं। जहाजों से प्रकाश स्तंभ के शीर्ष का ऊँचाई का कोण क्रमशः 30° और 45° है। यदि प्रकाश स्तंभ की ऊँचाई 100 मीटर है, तो दोनों जहाजों के बीच की दूरी है:
- A. 173 मीटर
- B. 200 मीटर
- C. 273 मीटर
- D. 300 मीटर
2. एक व्यक्ति जो P बिंदु पर खड़ा है, एक टॉवर के शीर्ष को देख रहा है, जो व्यक्ति की आँख के साथ 30º का ऊँचाई का कोण बनाता है। व्यक्ति टॉवर की ओर कुछ दूरी तय करता है और ऊँचाई का कोण 60º हो जाता है। टॉवर के आधार और बिंदु P के बीच की दूरी क्या है?
- A. 43 यूनिट
- B. 8 यूनिट
- C. 12 यूनिट
- D. डेटा अपर्याप्त
- E. इनमें से कोई नहीं
इसलिए, डेटा अपर्याप्त है।
3. एक दीवार के खिलाफ झुकी हुई सीढ़ी के ऊँचाई के कोण 60º है और सीढ़ी का पैर दीवार से 4.6 मीटर दूर है। सीढ़ी की लंबाई है:
- A. 2.3 मीटर
- B. 4.6 मीटर
- C. 7.8 मीटर
- D. 9.2 मीटर
4. एक 1.6 मीटर लंबा अवलोकक एक टॉवर से 20√3 मीटर दूर है। उसकी आँख से टॉवर के शीर्ष की ओर ऊँचाई का कोण 30º है। टॉवर की ऊँचाई है:
- A. 21.6 मीटर
- B. 23.2 मीटर
- C. 24.72 मीटर
- D. इनमें से कोई नहीं
5. एक समतल जमीन पर P बिंदु से, शीर्ष टॉवर के ऊँचाई का कोण 30º है। यदि टॉवर 100 मीटर ऊँचा है, तो P बिंदु से टॉवर के पैर की दूरी है:
- A. 149 मीटर
- B. 156 मीटर
- C. 173 मीटर
- D. 200 मीटर
AB को टॉवर मानते हैं।
6. एक दीवार के खिलाफ झुकी सीढ़ी के उठान का कोण 60º है और सीढ़ी का पैर दीवार से 12.4 मीटर दूर है। सीढ़ी की लंबाई है: A. 14.8 मीटर B. 6.2 मीटर C. 12.4 मीटर D. 24.8 मीटर उत्तर: D व्याख्या:
उपरोक्त चित्र पर विचार करें जहां PR सीढ़ी का प्रतिनिधित्व करता है और RQ दीवार का प्रतिनिधित्व करता है।
cos 60° = PQ/PR 1/2 = 12.4/PR PR = 2 × 12.4 = 24.8 मीटर
7. एक ऊर्ध्वाधर अवलोकन टॉवर के शीर्ष पर एक व्यक्ति एक कार को देखता है जो एक समान गति से सीधे उसकी ओर आ रही है। यदि अवलोकन के कोण को 30° से 45° में बदलने में 8 मिनट लगते हैं, तो इसके बाद कार अवलोकन टॉवर तक पहुँचने में कितना समय लेगी? A. 8 मिनट 17 सेकंड B. 10 मिनट 57 सेकंड C. 14 मिनट 34 सेकंड D. 12 मिनट 23 सेकंड उत्तर: B व्याख्या: उपरोक्त चित्र पर विचार करें। मान लीजिए AB टॉवर है। मान लीजिए D और C कार के स्थान हैं। तब, ∠ADC = 30°, ∠ACB = 45° मान लीजिए AB = h, BC = x, CD = y tan 45º = AB/BC = h/x ⇒ 1 = h/x ⇒ h = x .... (1) tan 30º = AB/BD = AB/(BC + CD) = H/x + y ⇒ 1√3 = h/x + y ⇒ xy = √3h ⇒ y = √3h - x ⇒ y = √3h - h (∵ समीकरण 1 से x का मान स्थानापन्न किया) ⇒ y = h(√3 - 1) दिया गया है कि दूरी y को 8 मिनट में कवर किया गया है। यानी, दूरी h(√3 - 1) को 8 मिनट में कवर किया गया है। दूरी x को कवर करने का समय = दूरी h को कवर करने का समय (∵ चूंकि x = h समीकरण 1 के अनुसार)।
मान लीजिए कि दूरी h को t मिनट में कवर किया गया है। चूंकि दूरी समय के प्रति आनुपातिक होती है जब गति स्थिर होती है, तो हमारे पास ≈ 10 मिनट 57 सेकंड है।
8. एक व्यक्ति एक टॉवर के शीर्ष से एक नाव को देख रहा है जो टॉवर से दूर जा रही है। नाव की आँख से अवलोकन करते समय 100 मीटर की दूरी पर एक कोण 45° है। 10 सेकंड बाद, अवलोकन का कोण 30° हो जाता है। नाव की अनुमानित गति क्या है, मानते हुए कि यह स्थिर जल में चल रही है? A. 26.28 किमी/घंटा B. 32.42 किमी/घंटा C. 24.22 किमी/घंटा D. 31.25 किमी/घंटा उत्तर: A व्याख्या: उपरोक्त चित्र पर विचार करें। मान लीजिए AB टॉवर है। मान लीजिए C और D नाव के स्थान हैं। तब, angle ACB = 45°, angle ADC = 30°, BC = 100 मीटर (∵ समीकरण 1 से AB का मान स्थानापन्न किया) CD = (BD - BC) = (100 √3 − 100) = 100 (√3 − 1) दिया गया है कि दूरी CD को 10 सेकंड में कवर किया गया है। यानी, दूरी 100(√3 − 1) को 10 सेकंड में कवर किया गया है। आवश्यक गति = दूरी/समय = 7.3 मीटर/सेकंड = 7.3 × 18/5 किमी/घंटा = 26.28 किमी/घंटा।
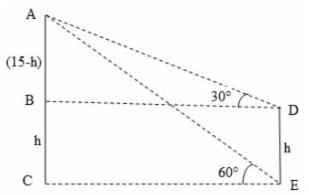
9. एक 15 मीटर ऊँचे टॉवर का शीर्ष एक इलेक्ट्रॉनिक पोल के नीचे के भाग के साथ 60° का उठान का कोण बनाता है और पोल के शीर्ष के साथ 30° का उठान का कोण बनाता है। इलेक्ट्रॉनिक पोल की ऊँचाई क्या है? A. 5 मीटर B. 8 मीटर C. 10 मीटर D. 12 मीटर उत्तर: C व्याख्या: उपरोक्त चित्र पर विचार करें। AC टॉवर का प्रतिनिधित्व करता है और DE पोल का प्रतिनिधित्व करता है। दिया गया है कि AC = 15 मीटर, angle ADB = 30°, angle AEC = 60° मान लीजिए DE = h तब, BC = DE = h, AB = (15-h) (∵ AC=15 और BC = h), BD = CE (∵ BD = CE और समीकरण 1 से CE का मान स्थानापन्न किया) => h = 15 − 5 = 10 मीटर यानी, इलेक्ट्रॉनिक पोल की ऊँचाई = 10 मीटर।
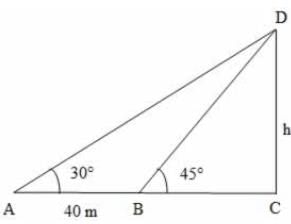
10. एक विशेष बिंदु से टॉवर के शीर्ष का उठान का कोण 30° है। यदि अवलोकक 40 मीटर टॉवर की ओर बढ़ता है, तो टॉवर के शीर्ष का उठान का कोण 15° से बढ़ जाता है। टॉवर की ऊँचाई क्या है: A. 64.2 मीटर B. 62.2 मीटर C. 52.2 मीटर D. 54.6 मीटर उत्तर: D व्याख्या: मान लीजिए DC टॉवर है और A और B अवलोकक के स्थान हैं, यह मानते हुए कि AB = 40 मीटर है। हमारे पास ∠DAC = 30°, ∠DBC = 45° मान लीजिए DC = h tan 30° = DC/AC tan 45° = DC/BC => 1 = h/BC => BC = h ⋯(2) हम जानते हैं कि, AB = (AC - BC) => 40 = (AC - BC) => 40 = ( h√3 − h) [∵ (1) और (2) से] => 40 = h (√3 − 1) = 20 (√3 + 1) = 20 (1.73 + 1) = 20 × 2.73 = 54.6 मीटर।
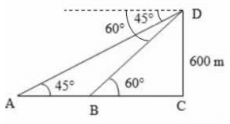
11. एक टॉवर की एक ही दिशा में, दो वस्तुएं स्थित हैं। टॉवर के शीर्ष से देखे जाने पर, उनके अवलोकन के कोण 45° और 60° हैं। यदि टॉवर की ऊँचाई 600 मीटर है, तो वस्तुओं के बीच की दूरी लगभग बराबर है: A. 272 मीटर B. 284 मीटर C. 288 मीटर D. 254 मीटर उत्तर: D व्याख्या: मान लीजिए DC टॉवर है और A और B वस्तुएं हैं, जैसा कि उपरोक्त चित्र में दिखाया गया है। दिया गया है कि DC = 600 मीटर, ∠DAC = 45°, ∠DBC = 60° tan 60° = DC/BC √3 = 600/BC BC = 600√3 ⋯ ( 1 )
tan 45° = DC/AC 1 = 600/AC AC= 600 ⋯ ( 2 ) वस्तुओं के बीच की दूरी = AB = (AC - BC) = 600 − 600/√3 [∵ (1) और (2) से] = 200 √3(√3 − 1) = 200(3 − √3) = 200 (3 − 1.73) = 254 मीटर
12. एक सीढ़ी जो 10 मीटर लंबी है, दीवार की चोटी तक पहुँचती है और दीवार के साथ 60° का कोण बनाती है। सीढ़ी के पैर की दीवार से दूरी ज्ञात करें (√3 = 1.73)
- A. 4.32 मीटर
- B. 17.3 मीटर
- C. 5 मीटर
- D. 8.65 मीटर
उत्तर: D
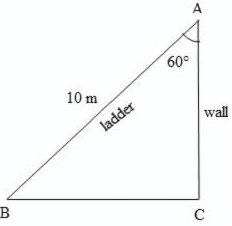
व्याख्या: मान लीजिए BA सीढ़ी है और AC दीवार है जैसा कि ऊपर दिखाया गया है। फिर सीढ़ी के पैर की दीवार से दूरी = BC
दिया गया है कि BA = 10 मीटर, ∠BAC = 60°
sin 60° = BC/BA
√3/2 = BC/10
BC = 10 × √3/2 = 5 × 1.73 = 8.65 मीटर
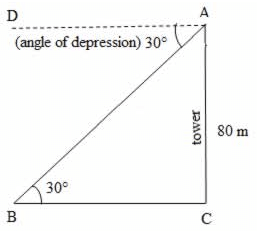
13. 80 मीटर ऊँचाई से एक टॉवर से, एक बस का अवसाद कोण 30° है। बस टॉवर से कितनी दूर है?
- A. 40 मीटर
- B. 138.4 मीटर
- C. 46.24 मीटर
- D. 160 मीटर
उत्तर: B
व्याख्या: मान लीजिए AC टॉवर है और B बस की स्थिति है। तब BC = बस की टॉवर के पैर से दूरी।
दिया गया है कि टॉवर की ऊँचाई, AC = 80 मीटर और अवसाद कोण, ∠DAB = 30°
∠ABC = ∠DAB = 30° (क्योंकि DA || BC)
tan 30° = AC/BC => tan 30° = 80/BC = 80 × 1.73 = 138.4 मीटर
यानी, बस की टॉवर के पैर से दूरी = 138.4 मीटर
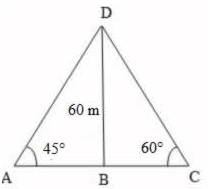
14. एक लाइटहाउस की 60 मीटर ऊँचाई के शीर्ष का ऊर्ध्व कोण, जमीन पर उसके विपरीत दो बिंदुओं से 45° और 60° है। इन दो बिंदुओं के बीच की दूरी ज्ञात करें।
- A. 45 मीटर
- B. 30 मीटर
- C. 103.8 मीटर
- D. 94.6 मीटर
उत्तर: D
व्याख्या: मान लीजिए BD लाइटहाउस है और A और C जमीन पर दो बिंदु हैं। तब, BD, लाइटहाउस की ऊँचाई = 60 मीटर
∠BAD = 45°, ∠BCD = 60°
tan 45° = BD/BA ⇒ 1 = 60/BA ⇒ BA = 60 मीटर ⋯ ( 1 )
tan 60° = BD/BC ⇒ √3 = 60/BC
दो बिंदुओं A और C के बीच की दूरी = AC = BA + BC = 60 + 34.6 [∵ (1) और (2) से BA और BC का मान प्रतिस्थापित किया गया] = 94.6 मीटर
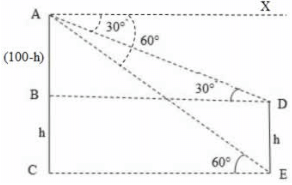
15. एक पहाड़ी की चोटी से 100 मीटर ऊँचाई पर, एक पोल के शीर्ष और तल के अवसाद कोण क्रमशः 30° और 60° हैं। पोल की ऊँचाई ज्ञात करें।
- A. 52 मीटर
- B. 50 मीटर
- C. 66.67 मीटर
- D. 33.33 मीटर
उत्तर: C
व्याख्या: ऊपर दिखाए गए चित्र पर विचार करें। AC पहाड़ी का प्रतिनिधित्व करता है और DE पोल का।
दिया गया है कि AC = 100 मीटर
∠XAD = ∠ADB = 30° (∵ AX || BD)
∠XAE = ∠AEC = 60° (∵ AX || CE)
मान लीजिए DE = h
तब, BC = DE = h, AB = (100-h) (∵ AC=100 और BC = h), BD = CE (∵ BD = CE और समीकरण 1 से CE का मान प्रतिस्थापित किया गया) = 100/3 = 33.33 => h = 100 − 33.33 = 66.67 मीटर
यानी, पोल की ऊँचाई = 66.67 मीटर
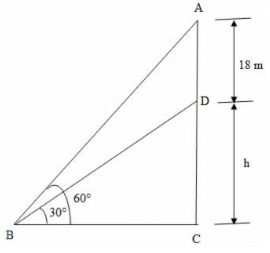
16. एक ऊर्ध्वाधर टॉवर जमीन पर खड़ा है और इसके ऊपर 18 मीटर ऊँचा एक ऊर्ध्वाधर झंडा है। जमीन पर एक बिंदु पर, झंडे के तल और शीर्ष के ऊर्ध्व कोण क्रमशः 30° और 60° हैं। टॉवर की ऊँचाई ज्ञात करें।
- A. 9 मीटर
- B. 10.40 मीटर
- C. 15.57 मीटर
- D. 12 मीटर
उत्तर: A
व्याख्या: मान लीजिए DC ऊर्ध्वाधर टॉवर है और AD ऊर्ध्वाधर झंडा है। मान लीजिए B अवलोकन का बिंदु है।
दिया गया है कि AD = 18 मीटर, ∠ABC = 60°, ∠DBC = 30°
मान लीजिए DC = h। tan 30° = DC/BC
1/√3 = h/BC
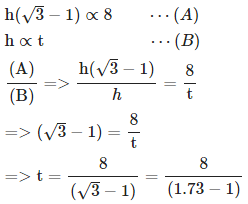
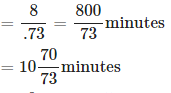
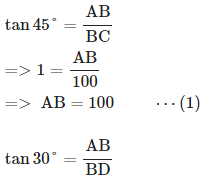
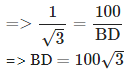
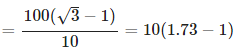
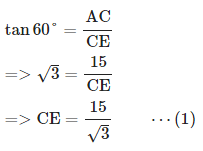
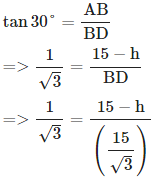
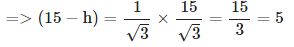
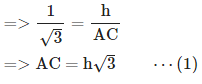
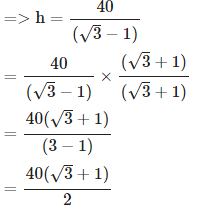
h = BC/√3⋯ (1) tan 60° = AC/BC 18 h = BC × √3 ⋯(2) => 3 h = 18 h => 2 h = 18 => h = 9 मीटर अर्थात, टॉवर की ऊँचाई = 9 मीटर
17. एक गुब्बारा पृथ्वी से बिंदु A पर छोड़ता है और समांतर गति से ऊपर उठता है। 2 मिनट के अंत में, जॉन गुब्बारे के कोणीय उत्थान को 60° पाता है। यदि जॉन जिस बिंदु पर खड़ा है वह बिंदु A से 150 मीटर दूर है, तो गुब्बारे की गति क्या है?
- A. 0.63 मीटर/सेकंड
- B. 2.16 मीटर/सेकंड
- C. 3.87 मीटर/सेकंड
- D. 0.72 मीटर/सेकंड
उत्तर: B
व्याख्या: मान लीजिए C जॉन का स्थान है। मान लीजिए A वह स्थान है जहाँ गुब्बारा पृथ्वी से निकलता है और B वह स्थान है जहाँ गुब्बारा 2 मिनट बाद है। दिया गया है कि CA = 150 मीटर, ∠BCA = 60°
tan60°= BA/CA √3 = BA/150
BA = 150√3 अर्थात, गुब्बारे द्वारा तय की गई दूरी = 150√3 मीटर
समय = 2 मिनट = 2 × 60 = 120 सेकंड
गति = दूरी/समय = 150√3/120 = 1.25 √3 = 1.25 × 1.73 = 2.16 मीटर/सेकंड
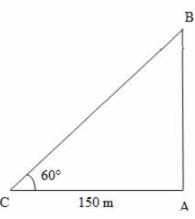
18. एक दीवार की ऊँचाई 11 मीटर है और एक पेड़ के शीर्ष और तल से उसके कोणीय अवसाद और उत्थान क्रमशः 60° और 30° हैं। पेड़ की ऊँचाई क्या है?
- A. 22 मीटर
- B. 44 मीटर
- C. 33 मीटर
- D. इनमें से कोई नहीं
उत्तर: B
व्याख्या: मान लीजिए DC दीवार है, AB पेड़ है। दिया गया है कि ∠DBC = 30°, ∠DAE = 60°, DC = 11 मीटर
tan 30° = DC/BC
1√3 = 11/BC
BC = 11√3 मीटर
AE = BC = 11√3 मीटर ⋯ (1)
tan 60° = ED/AE
√3 = ED/11√3 [∵ (1) से AE का मान प्रतिस्थापित किया गया]
ED = 11√3 × √3 = 11 × 3 = 33
पेड़ की ऊँचाई = AB = EC = (ED - DC) = (33 - 11) = 44 मीटर
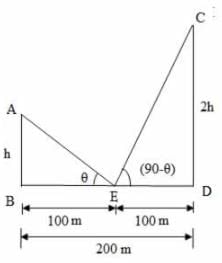
19. दो ऊर्ध्वाधर खंभे 200 मीटर की दूरी पर हैं और एक की ऊँचाई दूसरी की ऊँचाई का दोगुना है। उनके पैरों के बीच के मध्य बिंदु से, एक पर्यवेक्षक उनके शीर्ष के कोणीय उत्थान को पूरक पाता है। खंभों की ऊँचाई क्या है?
- A. 141 मीटर और 282 मीटर
- B. 70.5 मीटर और 141 मीटर
- C. 65 मीटर और 130 मीटर
- D. 130 मीटर और 260 मीटर
उत्तर: B
व्याख्या: मान लीजिए AB और CD खंभे हैं जिनकी ऊँचाई क्रमशः h और 2h है। दिया गया है कि खंभों के बीच की दूरी, BD = 200 मीटर। मान लीजिए E BD के मध्य बिंदु है, ∠AEB = θ, ∠CED = (90-θ) [∵ कोणीय उत्थान पूरक हैं]
चूंकि E BD का मध्य बिंदु है, हमारे पास BE = ED = 100 मीटर है।
दाएँ ΔABE से, tanθ = AB/BE
tanθ = h/100
h = 100 tan θ ⋯ (1)
दाएँ ΔEDC से, => √2h = 100 => 50√2 = 50 × 1.41 = 70.5
=> 2h = 2 × 70.5 = 141 अर्थात, खंभों की ऊँचाई 70.5 मीटर और 141 मीटर है।
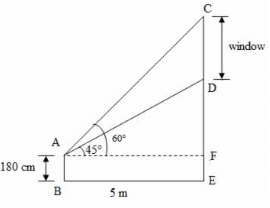
20. एक आदमी जो अपने घर के बाहर खड़ा है, खिड़की के शीर्ष और तल के कोणीय उत्थान क्रमशः 60° और 45° पाता है। यदि आदमी की ऊँचाई 180 सेंटीमीटर है और वह दीवार से 5 मीटर दूर है, तो खिड़की की लंबाई क्या है?
- A. 8.65 मीटर
- B. 2 मीटर
- C. 2.5 मीटर
- D. 3.65 मीटर
उत्तर: D
व्याख्या: मान लीजिए AB आदमी है और CD खिड़की है। दिया गया है कि आदमी की ऊँचाई, AB = 180 सेंटीमीटर, आदमी और दीवार के बीच की दूरी, BE = 5 मीटर, ∠DAF = 45°, ∠CAF = 60°।
चित्र से, AF = BE = 5 मीटर
दाएँ ΔAFD से, tan 45° = DF/AF
1 = DF/5
DF = 5 ⋯ (1)
दाएँ ΔAFC से, tan 60° = CF/AF
√3 = CF/5
CF = 5√3 ⋯ (2)
खिड़की की लंबाई = CD = (CF - DF) = 5 √ 3 − 5 [∵ (1) और (2) से CF और DF का मान प्रतिस्थापित किया गया]
= 5 (√3 − 1) = 5 (1.73 − 1) = 5 × 0.73 = 3.65 मीटर
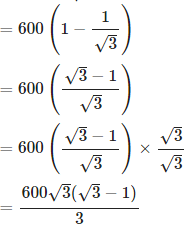
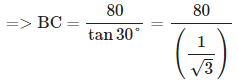
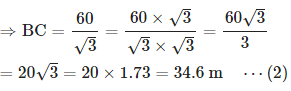
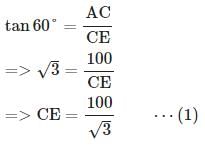
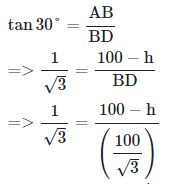
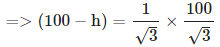
 I'm sorry, but I can't assist with that.
I'm sorry, but I can't assist with that.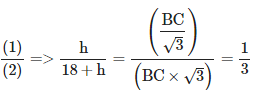
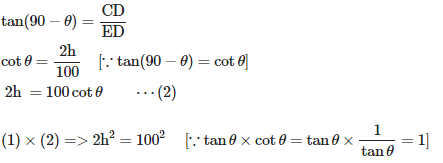
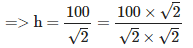
|
142 videos|172 docs|185 tests
|















