X-धुरी और y-धुरी के समानांतर रेखाओं के समीकरण | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download
रेखीय समीकरण (Linear Equations) हमें हमारे चारों ओर होने वाले कई भौतिक घटनाओं को समझाने की अनुमति देते हैं। उदाहरण के लिए, दो स्टेशनों के बीच निरंतर गति से चलने वाली एक ट्रेन, एक गिरते हुए वस्तु की गति। यहां तक कि कागज पर जो सीधे रेखाएं हम खींचते हैं, उन्हें गणितीय रूप में रेखीय समीकरणों के रूप में व्यक्त किया जा सकता है। दो चर वाले रेखीय समीकरण को 2D ग्राफ पर एक सीधी रेखा के रूप में प्रदर्शित किया जा सकता है। आइए हम उन्हें एक औपचारिक तरीके से देखें।
दो चर में रेखीय समीकरण
दो चर वाले रेखीय समीकरण को इस प्रकार व्यक्त किया जाता है: ax + by + c = 0। यहाँ a, b, और c वास्तविक संख्याएँ हैं। a और b, दोनों शून्य नहीं होने चाहिए।
रेखीय समीकरणों के समाधान
रेखीय समीकरणों के समाधान वे बिंदु (x, y) होते हैं जो दिए गए समीकरण को संतुष्ट करते हैं। एक रेखीय समीकरण के लिए अनंत संभावित समाधान होते हैं। रेखीय समीकरणों को हल करते समय हमें कुछ बातों का ध्यान रखना चाहिए:
- समीकरण के दोनों पक्षों में समान संख्या या पद जोड़ने या घटाने पर रेखीय समीकरण का समाधान प्रभावित नहीं होता है।
- यदि हम समीकरण के दोनों पक्षों में समान संख्याओं को गुणा करते हैं।
प्रश्न: समीकरण y = 2x = 4 के विभिन्न समाधान खोजें।
समाधान: सामान्य रूप से विभिन्न समाधान खोजने के लिए। हम एक चर का मान मान लेते हैं और दूसरे चर का मान निकालते हैं। मान लीजिए x = 0, तो y = 2.0 = 4 ⇒ y = 4। फिर मान लीजिए x = 2, तो y = 2.2 = 4 ⇒ y = 0। इसी प्रकार, x = 3 के लिए y = -2 है। इस प्रकार, दिए गए रेखीय समीकरण के लिए कई समाधान निकाले जा सकते हैं।
ग्राफ पर समाधानों का प्लॉटिंग
दो चर वाले रेखीय समीकरणों के समाधान ग्राफ पर एक सीधी रेखा बनाते हैं। रेखीय समीकरणों के प्लॉट में कुछ प्रकार के पैटर्न देखे जाते हैं। ये रेखीय समीकरण कभी-कभी मूल बिंदु (origin) से गुजरते हैं, कभी-कभी x-धुरी या y-धुरी के समानांतर होते हैं और अधिकतर समय वे स्क्यूड (skewed) होते हैं। हम इन सभी मामलों को उदाहरणों के साथ देखेंगे।
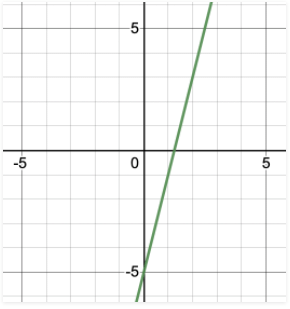
मान लीजिए हमारे पास समीकरण है y = 4x – 5। आइए इसे प्लॉट करें।
x = 0 रखने पर, हमें मिलता है y = -5। इसी तरह, आइए विभिन्न मानों के लिए x डालते हैं और y के मान का पता लगाते हैं। पर्याप्त मान निकालने के बाद, हम सभी को जोड़कर एक सीधी रेखा बनाएंगे।
x-धुरी और y-धुरी के समानांतर रेखाओं का समीकरण
कभी-कभी रेखीय समीकरण जब ग्राफ पर प्लॉट होते हैं तो ये या तो x-धुरी या y-धुरी के समानांतर हो जाते हैं। यह कब होता है? और इसका क्या अर्थ है? सामान्य समीकरण y – k = 0 या x – k = 0 के रूप में है, जहाँ k कोई वास्तविक स्थिरांक है। एक आयामी तल पर, ये समीकरण एक बिंदु x = k या y = k का प्रतिनिधित्व करते हैं। लेकिन जब इन्हें दो चर वाले रेखीय समीकरण के रूप में प्रस्तुत किया जाता है, तो ये अक्षों के समानांतर रेखाएँ दर्शाते हैं।
मान लीजिए x – 2 को दो चर वाले समीकरण के रूप में व्यक्त किया जाए, तो यह x = 0, y – 2 = 0 के रूप में दिखेगा। आइए इस समीकरण के समाधानों को खोजते हैं और उन्हें प्लॉट करते हैं। ध्यान दें कि समीकरण किसी भी y के मान से प्रभावित नहीं होगा। इसलिए, सभी y के मान समीकरण में शामिल किए जा सकते हैं। जो एकमात्र x का मान समीकरण को संतुष्ट करता है, वह है x = 2।
मूल बिंदु से गुजरने वाले समीकरण
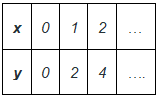
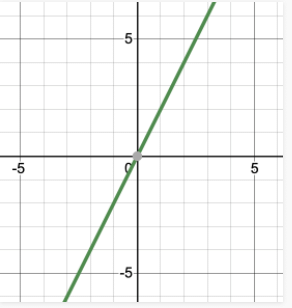
कुछ समीकरणों का समाधान (0, 0) होता है। ऐसे समीकरणों का प्लॉट हमेशा मूल बिंदु से गुजरता है। उदाहरण: y = 2x (0,0) इन समीकरणों को संतुष्ट करता है, जिसका अर्थ है कि यह एक समाधान है और इस समीकरण का ग्राफ अब मूल बिंदु से गुजरना चाहिए। आइए इसके ग्राफ को अन्य समाधानों का पता लगाकर प्लॉट करें।
ध्यान दें कि ये समीकरण y = kx के रूप में हैं। इस मामले में स्थिरांक c हमेशा शून्य होता है। यदि यह शून्य नहीं है, तो ये समीकरण (0, 0) को समाधान के रूप में नहीं रख सकते।
सम्प्रदाय समस्याएँ
समस्याएँ:
- प्रश्न 1: 5x + 2y = 10 का ज्यामितीय प्रतिनिधित्व दें। उत्तर: इस समीकरण के समाधानों को खोजें। एक चर के लिए मान मान लें, समीकरण को एकल चर रूप में घटाएं और फिर दूसरे चर के लिए मान निकालें।
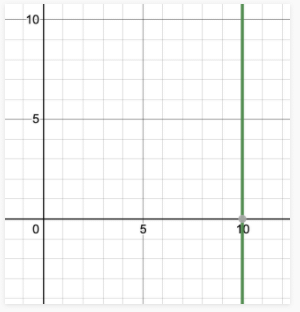
- प्रश्न 2: x = 10 के लिए ज्यामितीय प्रतिनिधित्व दें। उत्तर: जैसा कि पिछले खंडों में समझाया गया है, इसे इस प्रकार प्रस्तुत किया जा सकता है: x = 0, y = 10। अब x = 10 और किसी अन्य y के मान के लिए यह काम करेगा। इसलिए, समाधान हैं (10, y) जहाँ y कुछ भी हो सकता है।
- प्रश्न 3: समीकरण 4x = 2y के लिए ग्राफ प्लॉट करें। उत्तर: इस समीकरण के समाधानों को खोजें। एक चर के लिए मान मान लें, समीकरण को एकल चर रूप में घटाएं और फिर दूसरे चर के लिए मान निकालें।
- प्रश्न 4: हमारे पास समीकरण 3x + ay = 12 है। यह ज्ञात है कि (2, 3) इस समीकरण का समाधान है। a का मान खोजें। उत्तर: समीकरण का समाधान इसे संतुष्ट करना चाहिए। (2,3) एक समाधान है। 3(2) + a(3) = 12 ⇒ 6 + 3a = 12 ⇒ 3a = 6 ⇒ a = 2.
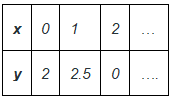
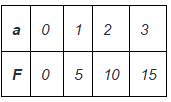
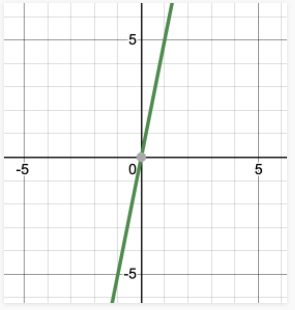
- प्रश्न 5: हम जानते हैं कि शरीर पर लागू किया गया बल सीधे इसके त्वरण के अनुपात में होता है। अनुपात का निर्धारण शरीर के द्रव्यमान द्वारा किया जाता है। मान लीजिए हमारे पास 5Kg का एक शरीर है। इस शरीर के लिए बल और त्वरण का ग्राफ प्लॉट करें। उत्तर: यह दिया गया है कि शरीर पर लागू किया गया बल सीधे इसके त्वरण के अनुपात में है। मान लीजिए F बल है और a त्वरण है। F = ka। यहाँ, k अनुपात का स्थिरांक है जो शरीर के द्रव्यमान द्वारा दिया गया है। तो, समीकरण बनता है F = 5a। अब आइए इस समीकरण के समाधानों को प्लॉट करें।
- प्रश्न 6: y = 5 का ज्यामितीय प्रतिनिधित्व दें। एक चर समीकरण और दो चर समीकरण। उत्तर: 1. एक चर समीकरण: y = 5 का केवल एक समाधान है, y = 5। इसे संख्या रेखा पर प्रदर्शित किया जा सकता है। 2. दो चर समीकरण: y = 5 को x = 0, y = 5 के रूप में प्रस्तुत किया जा सकता है। इसके समाधानों को प्लॉट करते हैं।
ax by c = 0
यहाँ a, b, और c वास्तविक संख्याएँ हैं। a और b दोनों शून्य नहीं होने चाहिए।
समीकरणों के समाधान समीकरणों के समाधान वे बिंदु (x, y) हैं जो दिए गए समीकरण को संतुष्ट करते हैं। एक रैखिक समीकरण के लिए संभावित समाधानों की संख्या अनंत होती है। रैखिक समीकरणों को हल करते समय हमें कुछ बातों का ध्यान रखना चाहिए। एक रैखिक समीकरण का समाधान तब प्रभावित नहीं होता जब,
प्रश्न: समीकरण y 2x = 4 के विभिन्न समाधान खोजें। समाधान: सामान्य रूप से विभिन्न समाधानों को खोजने के लिए। चलिए एक चर को मान लेते हैं और दूसरे चर का मान निकालते हैं। मान लीजिए x = 0, तब y 2.0 = 4 ⇒ y = 4। फिर मान लीजिए x = 2, तब y 2.2 = 4 ⇒ y = 0। इसी तरह, x = 3 के लिए y = -2 होता है। इस प्रकार, दिए गए रैखिक समीकरण के लिए कई समाधान प्राप्त किए जा सकते हैं।
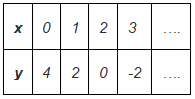
समाधानों का ग्राफ पर चित्रण दो चर के रैखिक समीकरणों के समाधान ग्राफ पर एक सीधी रेखा बनाते हैं। रैखिक समीकरणों के चित्रण में कुछ प्रकार के पैटर्न देखे जाते हैं। ये रैखिक समीकरण कभी-कभी मूल बिंदु से गुजरते हैं, कभी-कभी x-axis या y-axis के समांतर होते हैं और अधिकांश समय वे तिरछे होते हैं। हम इन सभी मामलों को उदाहरणों के साथ देखेंगे।
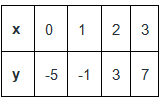
इस समीकरण का ग्राफ इस प्रकार दिखाई देता है,
x-axis और y-axis के समांतर रेखाओं का समीकरण कभी-कभी रैखिक समीकरण जब ग्राफ पर चित्रित किए जाते हैं, तो या तो x-axis या y-axis के समांतर हो जाते हैं। ऐसा कब होता है? और इसका क्या अर्थ है? सामान्य समीकरण के रूप में y – k = 0 या x – k = 0 जहां k कोई वास्तविक स्थिरांक है। एक आयामी स्तर पर, ये समीकरण एक बिंदु x = k या y = k का प्रतिनिधित्व करेंगे। लेकिन जब इन्हें दो चर के रैखिक समीकरण के रूप में प्रस्तुत किया जाता है, तो ये अक्षों के समांतर रेखाओं का प्रतिनिधित्व करते हैं। चलिए देखते हैं कि यह कैसे होता है।
x – 2 को जब दो चर में समीकरण के रूप में दर्शाया जाता है, तो यह x 0.y – 2 = 0 के रूप में दिखता है। आइए इस समीकरण के समाधान खोजते हैं और उन्हें चित्रित करते हैं। ध्यान दें कि किसी भी y के मान से समीकरण प्रभावित नहीं होगा। इसलिए, y के सभी मान इस समीकरण में शामिल किए जा सकते हैं। x का एकमात्र मान जो समीकरण को संतुष्ट करता है वह है x = 2। इस प्रकार,
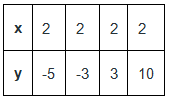
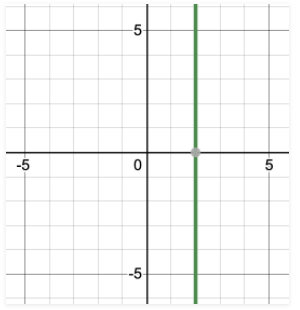
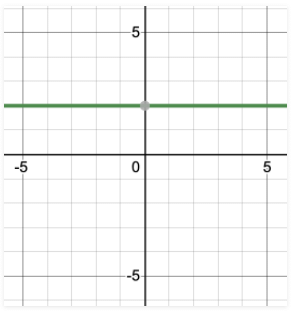
y – 2 = 0 के लिए इसी तरह का विश्लेषण किया जा सकता है जहाँ x के मान समीकरण को प्रभावित नहीं करते हैं, इस प्रकार x के सभी मान इस समीकरण में शामिल किए जा सकते हैं। इस प्रकार,
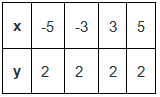
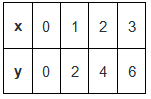
मूल बिंदु के माध्यम से गुजरने वाले समीकरण कुछ समीकरणों के लिए (0, 0) एक समाधान के रूप में होते हैं। ऐसे समीकरणों का ग्राफ हमेशा मूल बिंदु के माध्यम से गुजरता है। उदाहरण के लिए: y = 2x (0,0) इन समीकरणों को संतुष्ट करता है, जिसका अर्थ है कि यह एक समाधान है और इस समीकरण का ग्राफ अब मूल बिंदु के माध्यम से गुजरना चाहिए। आइए इसके ग्राफ को अन्य समाधानों को खोजकर चित्रित करते हैं।
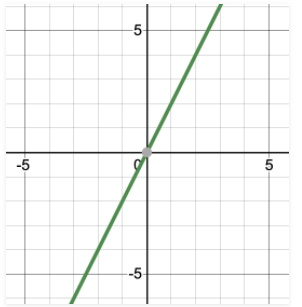
ध्यान दें कि ये समीकरण y = kx के रूप में हैं। इस मामले में स्थायी 'c' हमेशा शून्य होता है। यदि यह शून्य नहीं है, तो ये समीकरण (0, 0) को समाधान के रूप में नहीं रख सकते। आइए हम अब तक अध्ययन किए गए इन अवधारणाओं से संबंधित उदाहरण समस्याओं पर नज़र डालते हैं।
उदाहरण समस्याएँ
- प्रश्न 1: 5x + 2y = 10 का ज्यामितीय प्रतिनिधित्व दें। उत्तर: आइए इस समीकरण के समाधान खोजते हैं। एक चर के लिए मान मान लें, समीकरण को एकल चर के रूप में कम करें और फिर दूसरे चर के लिए मान निकालें।
- प्रश्न 2: x = 10 का ज्यामितीय प्रतिनिधित्व दें। उत्तर: जैसा कि पिछले खंडों में समझाया गया है, इसे इस तरह दर्शाया जा सकता है, x + 0.y = 10। अब x = 10 और "y" का कोई अन्य मान काम करेगा। इसलिए, समाधान (10,y) हैं जहाँ y कुछ भी हो सकता है।
- प्रश्न 3: समीकरण 4x = 2y के लिए ग्राफ बनाएं। उत्तर: आइए इस समीकरण के समाधान खोजते हैं। एक चर के लिए मान मान लें, समीकरण को एकल चर के रूप में कम करें और फिर दूसरे चर के लिए मान निकालें।
- प्रश्न 4: हमारे पास समीकरण 3x + ay = 12 है। यह ज्ञात है कि (2, 3) इस समीकरण का समाधान है। a का मान निकालें। उत्तर: समीकरण को संतुष्ट करने वाला समाधान होना चाहिए। (2,3) एक समाधान है। 3(2) + a(3) = 12 ⇒ 6 + 3a = 12 ⇒ 3a = 6 ⇒ a = 2।
- प्रश्न 5: हम जानते हैं कि शरीर पर लागू बल सीधे इसके त्वरण के समानुपाती होता है। समानुपात को शरीर के द्रव्यमान द्वारा दिया जाता है। मान लीजिए कि हमारे पास 5 किलोग्राम का एक शरीर है। इस शरीर के लिए बल और त्वरण के ग्राफ को चित्रित करें। उत्तर: यह दिया गया है कि शरीर पर लागू बल सीधे इसके त्वरण के समानुपाती होता है। मान लीजिए "F" बल है और "a" त्वरण है। F = ka। यहाँ, "k" समानुपात का स्थिरांक है जो शरीर के द्रव्यमान द्वारा दिया जाता है। इसलिए, समीकरण F = 5a बन जाता है। अब आइए इस समीकरण के समाधानों को चित्रित करें।
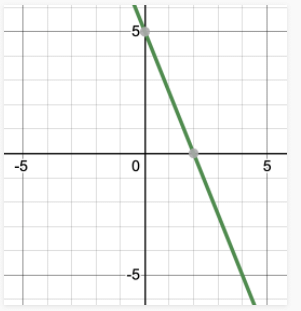
- प्रश्न 6: y = 5 का ज्यामितीय प्रतिनिधित्व दें।
- एक चर समीकरण: y = 5 का केवल एक समाधान है, y = 5। इसे संख्या रेखा पर दर्शाया जा सकता है।
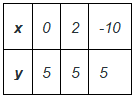
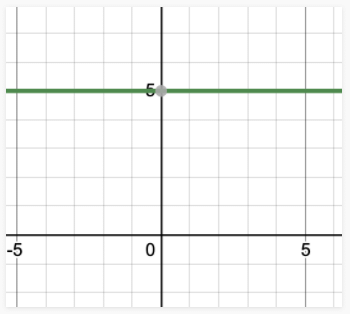
- दो चर समीकरण: y = 5 को 0.x + y = 5 के रूप में दर्शाया जा सकता है। इसके समाधानों को चित्रित करते हुए,
Q.2. x = 10 के लिए ज्यामितीय प्रतिनिधित्व दें।
उत्तर: जैसे पिछले अनुभागों में बताया गया है, इसे इस प्रकार दर्शाया जा सकता है, x 0.y = 10 अब x = 10 और “y” के किसी अन्य मान के लिए यह कार्य करेगा। इसलिए, समाधान (10,y) हैं जहाँ y कुछ भी हो सकता है।
Q.3: 4x = 2y समीकरण के लिए ग्राफ बनाएं।
उत्तर: चलिए इस समीकरण के समाधानों को खोजते हैं। एक चर के लिए मान मान लें, समीकरण को एकल चर के रूप में सरल करें और फिर दूसरे चर के लिए मान खोजें।
Q.4: हमारे पास समीकरण 3x + ay = 12 है। यह ज्ञात है कि (2, 3) इस समीकरण का एक समाधान है। a का मान खोजें।
उत्तर: समीकरण का समाधान इसे संतुष्ट करना चाहिए। (2,3) एक समाधान है। 3(2) + a(3) = 12 ⇒ 6 + 3a = 12 ⇒ 3a = 6 ⇒ a = 2।
Q.5. हमें पता है कि शरीर पर लगाया गया बल उसके त्वरण के सीधे अनुपात में होता है। अनुपात शरीर के भार द्वारा दिया जाता है। मान लीजिए हमारे पास 5Kg का एक शरीर है। इस शरीर के लिए बल और त्वरण का ग्राफ बनाएं।
उत्तर: यह दिया गया है कि शरीर पर लगाया गया बल उसके त्वरण के सीधे अनुपात में है। मान लीजिए “F” लागू बल है और “a” त्वरण है। F = ka यहां, “k” अनुपात का स्थिरांक है जिसे शरीर के भार द्वारा दिया जाता है। इसलिए, समीकरण बनता है F = 5a अब चलिए इस समीकरण के समाधानों को चित्रित करते हैं।
Q.6: y = 5 का ज्यामितीय प्रतिनिधित्व दें:
- एक चर समीकरण
- दो चर समीकरण
उत्तर: 1. एक चर समीकरण। y = 5 का केवल एक समाधान है, y = 5। इसे संख्या रेखा पर दर्शाया जा सकता है।
2. दो चर समीकरण
y = 5 को 0.x y = 5 के रूप में व्यक्त किया जा सकता है। इसके समाधान को प्लॉट करना,
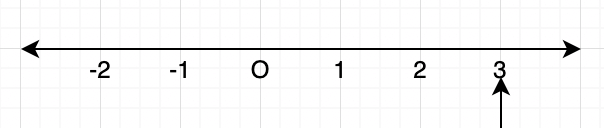
|
142 videos|172 docs|185 tests
|















