सारांश और उदाहरण: संख्या श्रृंखला | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download
| Table of contents |

|
| प्रकार 2: पूर्ण वर्ग या पूर्ण घन |

|
| प्रकार 3: गुणनखंडन / अभाज्य गुणनखंडन |

|
| प्रकार 4: फिबोनाच्ची श्रेणी |

|
| प्रकार 5: अंकों का योग |

|
| प्रकार 14: वैकल्पिक श्रृंखला |

|
संख्याओं की श्रृंखला (Number Series) प्रतियोगी परीक्षाओं में एक महत्वपूर्ण विषय है, जिसमें इस खंड के लिए विशेष रूप से पाँच प्रश्न समर्पित होते हैं। यह विभिन्न परीक्षाओं में महत्वपूर्ण स्थान रखता है। प्रतियोगी परीक्षाओं की तैयारी कर रहे उम्मीदवार केवल 2-3 मिनट में संख्याओं की श्रृंखला के विभिन्न प्रकारों और पैटर्न को समझकर 4-5 अंक प्राप्त कर सकते हैं।
संख्याओं की श्रृंखला क्या है?
- संख्याओं की श्रृंखला एक प्रकार का अनुक्रम है, जहाँ कुछ संख्याएँ गलती से संख्याओं की श्रृंखला में डाली गई होती हैं और उस श्रृंखला में कुछ संख्या गायब होती है। हमें पहले अवलोकन करना होता है और फिर उस श्रृंखला के लिए सही संख्या खोजना होता है।
- प्रश्न यह भी हो सकते हैं जहाँ आपको श्रृंखला को जारी रखने या श्रृंखला के तत्काल अगले पद का निर्धारण करना होता है। अनुक्रम उन संख्याओं की सूची है जो एक विशिष्ट क्रम में लिखी जाती हैं।
संख्याओं की श्रृंखला के सामान्य प्रकार

प्रकार 1: जोड़ना / घटाना या गुणा / भाग करना
ये श्रृंखलाएँ सम या विषम संख्याओं के जोड़ने या घटाने के पैटर्न का पालन करती हैं।
उदाहरण 1: निम्नलिखित श्रृंखला में प्रश्न चिह्न के स्थान पर क्या आना चाहिए: 19, 23, 39, 75, ?, 239।
- संख्याओं की श्रृंखला को हल करने का सबसे सामान्य तरीका दो आसन्न संख्याओं के बीच के अंतर की जाँच करना है, लेकिन अंतर केवल जोड़ने/घटाने तक सीमित नहीं होता, बल्कि यह गुणा/भाग के साथ भी हो सकता है। इसलिए, यह जानने के लिए कि बढ़ती श्रृंखला में जोड़ने या गुणा करने पर विचार करना है, पहले और अंतिम संख्या के बीच के अंतर की मदद से अनुमान लगाना चाहिए।
- यदि अंतर पहले और अंतिम संख्या को बनाने के लिए उपयोग किए गए चरणों के अनुसार कम लगता है, तो हमें जोड़ने की जाँच करनी चाहिए। यदि अंतर बड़ा या बहुत बड़ा लगता है, तो हमें आसन्न संख्याओं के बीच गुणा करने की ट्रिक की जाँच करनी चाहिए।
उदाहरण 1 में, पहले नंबर (19) और अंतिम नंबर (239) के बीच का अंतर 220 है।
अब एक सवाल उठेगा कि हम कैसे मान लेंगे कि अंतर अधिक है या कम। हम इसे पहले संख्या से अंतिम संख्या तक पहुंचने के लिए आवश्यक कदमों की संख्या को ध्यान में रखकर मान लेंगे।
- उदाहरण 1 में, 19 को 239 में पांच कदमों में बदला जाता है, क्योंकि उनके बीच चार और संख्या हैं, जिनमें से हमें एक को पता करना है।
- 19 और 239 के बीच 220 का अंतर पांच कदमों में तार्किक रूप से बढ़ती श्रृंखला में गुणन की तुलना में जोड़ने को प्राथमिकता देता है।
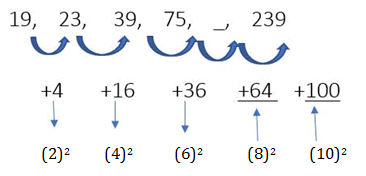
- 75 + 64 = 139, 139 + 100 = 239, 139 सही उत्तर है।
उदाहरण 2: निम्नलिखित श्रृंखला में प्रश्न चिह्न के स्थान पर क्या आना चाहिए: 10, 31, 95, 288, ?, 2609।
जैसा कि हम ऊपर के उदाहरण में देख सकते हैं, पहले संख्या (10) और अंतिम संख्या (2609) के बीच का अंतर 2599 है, जो हमें संख्याओं के बीच गुणन की चाल की जांच करने के लिए संकेत करता है।

(288*3) + 4 = 868, सही उत्तर है।
नोट: गुणन की चाल की जांच करते समय हमेशा श्रृंखला के दाहिने सिरे से शुरू करें।
उदाहरण 3: निम्नलिखित श्रृंखला में प्रश्न चिह्न के स्थान पर क्या आना चाहिए: 30, 34, 43, 59, 84, 120, ?। (क) 169 (ख) 148 (ग) 153 (घ) 176 (ङ) इनमें से कोई नहीं
सही उत्तर विकल्प (क) है। दिए गए पैटर्न हैं:
4, 9, 16, 25 और इसी तरह। तो, गायब संख्या 169 = 120 + 49 है।
उदाहरण 4: निम्नलिखित श्रृंखला में प्रश्न चिह्न के स्थान पर क्या आना चाहिए: 40, 54, 82, ?, 180, 250। (क) 142 (ख) 124 (ग) 136 (घ) 163 (ङ) इनमें से कोई नहीं
सही उत्तर विकल्प (c) है। पैटर्न है: 14, 28, 42, 56, 70। इसलिए, गायब संख्या 82 है। 42 = 124
उदाहरण 5: नीचे दिए गए श्रृंखला में गलत संख्या खोजें: 0, 1, 3, 8, 18, 35, 264 (क) 62 (ख) 35 (ग) 18 (घ) 8 (ङ) इनमें से कोई नहीं
लगातार संख्याओं के बीच अंतर में एक पैटर्न है:
0 - 1 = 1 ← 02
1 - 3 = 2 ← 12
3 - 8 = 5 ← 22
8 - 18 = 10 ← 32
18 - 35 = 17 ← 42
अगला अंतर 52 होना चाहिए, अर्थात् 26। 35 - 61 = 26 ← 52
इससे, सही क्रम होगा: 0, 1, 3, 8, 18, 35, 61 और इसलिए, गलत संख्या है: 264
उदाहरण 6: नीचे दिए गए श्रृंखला में गलत संख्या खोजें: 5531, 5506, 5425, 5304, 5135, 4910, 4621 (क) 5531 (ख) 5425 (ग) 4621 (घ) 5135 (ङ) 5506
संख्या को 5531 के स्थान पर 5555 होना चाहिए। -72, -92, -112, -132, -152, -172…
उदाहरण 7: नीचे दिए गए श्रृंखला में गलत संख्या खोजें: 6, 7, 9, 13, 26, 37, 69 (क) 7 (ख) 26 (ग) 69 (घ) 37 (ङ) 9
सही उत्तर विकल्प (ख) है।
संख्या को 26 के स्थान पर 21 होना चाहिए। पैटर्न है: 1, 2, 4, 8, 16, 32
उदाहरण 8: नीचे दिए गए श्रृंखला में गलत संख्या खोजें: 1, 3, 10, 36, 152, 760, 4632 (क) 3 (ख) 36 (ग) 4632 (घ) 760 (ङ) 152
सही उत्तर विकल्प (घ) है।
संख्या को 760 के स्थान पर 770 होना चाहिए। पैटर्न है: ×1 2, ×2 4, ×3 6, ×4 8, ×5 10, ×6 12, …
प्रकार 2: पूर्ण वर्ग या पूर्ण घन
प्रकार 2: पूर्ण वर्ग या पूर्ण घन
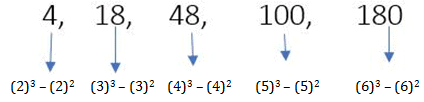
प्रश्न: 4, 18, 48, 100, 180, ___।
- यदि प्रकार-1 किसी श्रेणी में लागू नहीं होता है, तो अगले चरण में हमें दिए गए संख्याओं या उनके अंतर की तुलना प्राकृतिक संख्याओं के वर्ग या घन से करनी चाहिए, जैसा कि उपरोक्त उदाहरण में किया गया है। अतः, (7)³ - (7)² = 294, सही उत्तर है।
(क) पूर्ण वर्ग श्रृंखला:
(क) पूर्ण वर्ग श्रृंखला:
यह प्रकार की श्रृंखला एक संख्या के वर्ग पर आधारित होती है जो समान क्रम में होती है और उस दी गई श्रृंखला में एक वर्ग संख्या गायब होती है।
उदाहरण 11: निम्नलिखित विकल्पों में, कुछ संख्या श्रृंखलाएँ हैं। इनमें से एक में त्रुटि है, गलत संख्या का चयन करें:
(क) 3, 9, 15, 21
(ख) 9, 81, 225, 441
(ग) 441, 529, 676, 841
(घ) 900, 841, 784, 729
उत्तर: (ग)
समाधान: पहली श्रृंखला केवल एक ए.पी. है जिसमें सामान्य अंतर 6 है। अब, हम देख सकते हैं कि दूसरी श्रृंखला पूर्ण वर्ग श्रृंखला है। यह श्रृंखला विकल्प (क) में दी गई श्रृंखला से बनाई जा सकती है। तीसरी श्रृंखला एक दो-स्तरीय वर्ग श्रृंखला है लेकिन 841 की जगह हमें 900 होना चाहिए। यह गलत श्रृंखला है। अंतिम श्रृंखला भी एक वर्ग श्रृंखला है। इसलिए चार प्रस्तुत विकल्पों में सही विकल्प या गलत श्रृंखला C) 441, 529, 676, 841 है।
उदाहरण 12: निम्नलिखित श्रृंखला में प्रश्न चिह्न के स्थान पर क्या आना चाहिए: 841, ?, 2401, 3481, 4761 उत्तर: ये संख्याएँ कुछ पूर्णांकों के वर्ग हैं:
292, 392, 492, 592, 692
अतः गायब संख्या 392 = 1521 है।
उदाहरण 13: निम्नलिखित श्रृंखला में प्रश्न चिह्न के स्थान पर क्या आना चाहिए: 1, 9, 25, ?, 81, 121 उत्तर: 12, 32, 52, 72, 92, 112 गायब संख्या 49 है।
उदाहरण 14: निम्नलिखित श्रृंखला में प्रश्न चिह्न के स्थान पर क्या आना चाहिए: 289, 225, 169, ?, 81 उत्तर: 172, 152, 132, 112, 92
गायब संख्या 121 है।
(b) पूर्ण घन श्रृंखला:
(b) पूर्ण घन श्रृंखला:
इस प्रकार की श्रृंखला एक संख्या के घन पर आधारित होती है जो समान क्रम में होती है और उस दी गई श्रृंखला में एक घन संख्या गायब होती है। उदाहरण 15: निम्नलिखित श्रृंखला में प्रश्न चिह्न के स्थान पर क्या आना चाहिए: 3375, ?, 24389, 46656, 79507 उत्तर: 153, 223, 293, 363, 433 (प्रत्येक घन अंक में सात जोड़कर अगली घन संख्या प्राप्त होती है)
गायब संख्या 10648 है।
उदाहरण 16: निम्नलिखित श्रृंखला में प्रश्न चिह्न के स्थान पर क्या आना चाहिए: 729, 6859, 24389, ?, 117649, 205379 उत्तर: 93, 193, 293, 393, 493, 593
गायब संख्या 59319 है।
उदाहरण 17: निम्नलिखित श्रृंखला में प्रश्न चिह्न के स्थान पर क्या आना चाहिए: 1000, 8000, 27000, 64000, ? उत्तर: 103, 203, 303, 403, 503
गायब संख्या 125000 है।
प्रकार 3: गुणनखंडन / प्राथमिक गुणनखंडन
प्रकार 3: गुणनखंडन / अभाज्य गुणनखंडन
- यदि प्रकार 1 और प्रकार 2 एक अनुक्रम में लागू नहीं होते हैं, तो अगले चरण में संख्याओं के गुणनखंड बनाने का प्रयास करना चाहिए।
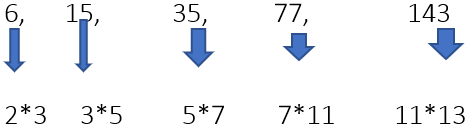
उदाहरण 18: 6, 15, 35, 77, 143, __। उपरोक्त उदाहरण में, उत्तर प्राप्त करने के लिए सभी पूर्ववर्ती तरीके लागू नहीं होते। इसलिए, हम दी गई संख्याओं के गुणनखंड बनाएंगे। (2, 3, 5, 7, 11, 13) ये सभी अभाज्य संख्या हैं, आरोही क्रम में। इसलिए, 13*17 = 221, सही उत्तर है।
प्रकार 4: फिबोनाच्ची श्रेणी
प्रकार 4: फिबोनाच्ची श्रेणी
- एक श्रृंखला जिसमें एक संख्या पिछले दो संख्याओं का उपयोग करके बनाई जाती है, उसे फिबोनाच्ची श्रृंखला कहा जाता है।
उदाहरण 19: 1, 4, 5, 9, 14, 23, ___ उपरोक्त अनुक्रम में, सभी संख्याएँ पिछले दो संख्याओं का योग हैं। इसलिए, 23 + 14 = 37, सही उत्तर है।
प्रकार 5: अंकों का योग
प्रकार 5: अंकों का योग
उदाहरण 20: उपरोक्त अनुक्रम में, दो अंकों के बीच का अंतर पहले अंक के अंकों का योग है। इसलिए, 89 17 = 106, सही उत्तर है।

उदाहरण 21: सभी अंकों को उनके योग से गुणा किया जाता है या उनके योग से बारी-बारी से जोड़ा जाता है। इसलिए, 11788 25 = 11813, सही उत्तर है।
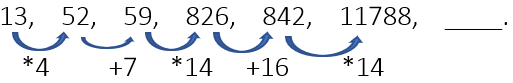
प्रकार 6: वैकल्पिक पैटर्न श्रृंखला
- जब प्रश्न में दिए गए अंकों की संख्या अधिक होती है या जब प्रश्न श्रृंखला के दो अंकों या एक ही अंक के श्रृंखला में दो बार आने का संकेत देता है, तो ये सभी वैकल्पिक पैटर्न श्रृंखला का संकेत देते हैं।
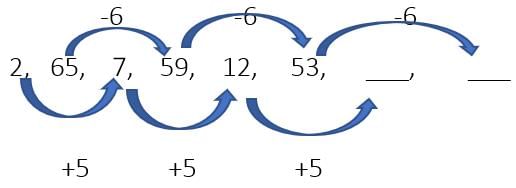
उदाहरण 22: तो, अंकों हैं 12 5 = 17, 53-6 = 47 उत्तर। 17, 47
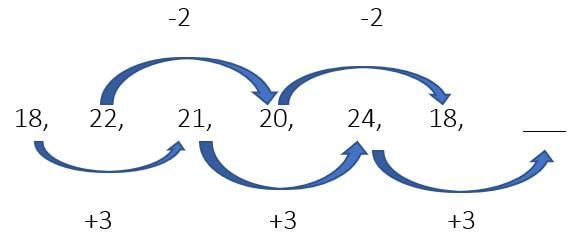
उदाहरण 23: तो, अंक है 24 3 = 27 उत्तर। 27
प्रकार 7: दशमलव पैटर्न श्रृंखला
जब अनुक्रम के अंकों को दशमलव रूप में दिया जाता है, तो यह दशमलव पैटर्न श्रृंखला होती है। उदाहरण 24: तो, उत्तर है 18 * 0.8 = 14.4

उदाहरण 25: 16, 24, 60, 210, 945, __ पैटर्न है: 16 x 1.5 = 24 24 x 2.5 =60 60 x 3.5 = 210 210 x 4.5 = 945 945 x 5.5 = 5197.5
प्रकार 8: ब्रैकेट पैटर्न श्रृंखला
ब्रैकेट पैटर्न का उपयोग करते समय हम पहले बाहर से गुणा करते हैं और दिए गए संख्या के आधार पर या तो जोड़ते हैं या घटाते हैं।
उदाहरण 26: 3, 28, 180, ____, 3676 पैटर्न है: (3 1)x7 = 28 (28 2)x6 =180 (180 3)x5 = 915 (915 4)x4 = 3676 उत्तर। 915
उदाहरण 27: 37, 31, 52, 144, __, 2810 पैटर्न है: (37-6)x1=31 (31-5)x2=52 (52-4)x3=144 (144-3)x4=564 (564-2)x5=2810 उत्तर। 564
प्रकार 9: डुअल पैटर्न श्रृंखला
उदाहरण 28: 15, 9, 8, 12, 36, 170 19, a, b, __, d, e, पैटर्न है: (15-6)x1=9 (9-5)x2=8 (8-4)x3=12 इसी तरह: (19-6)x1=13 (13-5)x2=16 (16-4)x3=36 उत्तर। 36
प्रकार 10: फैक्टोरियल आधारित श्रृंखला
यह नवीनतम परीक्षा में पूछे गए प्रश्नों का एक नया पैटर्न है।
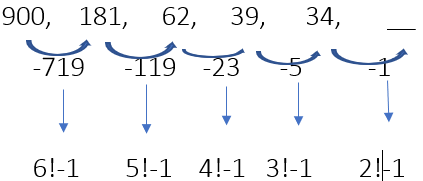
उदाहरण 29: उत्तर: 33
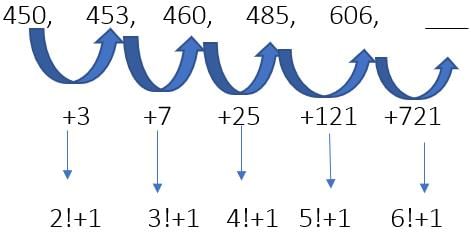
उदाहरण 30: उत्तर: 606 721 = 1327
प्रकार 11: अंकगणितीय श्रृंखला
एक श्रृंखला जिसमें अगला पद पिछले पद में एक निश्चित संख्या जोड़कर या घटाकर प्राप्त किया जाता है।
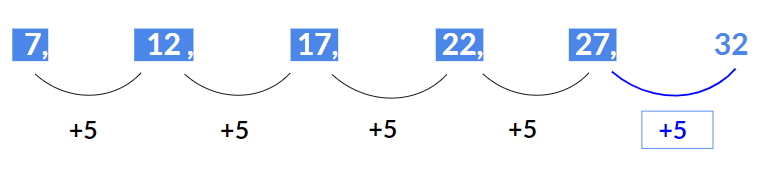
उदाहरण 1: अगला पद ज्ञात करें 7, 12, 17, 22, 27, ? समाधान: उपर्युक्त श्रृंखला एक अंकगणितीय श्रृंखला है जहाँ प्रत्येक पद में 5 जोड़ा जाता है। अर्थात:
- 12 = 7 + 5
- 17 = 12 + 5
- 22 = 17 + 5
- 27 = 22 + 5
अतः अगला पद होगा 27 + 5 = 32।
उदाहरण 2: गायब पद लिखें 29, 23, 17, 11, ? समाधान: उपर्युक्त श्रृंखला एक अंकगणितीय श्रृंखला है जहाँ प्रत्येक पद से 6 घटाया जाता है। अर्थात:
- 29 – 6 = 23
- 23 – 6 = 17
- 17 – 6 = 11
अतः अगला पद होगा 11 - 6 = 5।
प्रकार 11: ज्यामितीय श्रृंखला
एक श्रृंखला जहाँ प्रत्येक अगली संख्या को पिछले संख्या को एक विशेष संख्या से गुणा या भाग देकर प्राप्त किया जाता है।
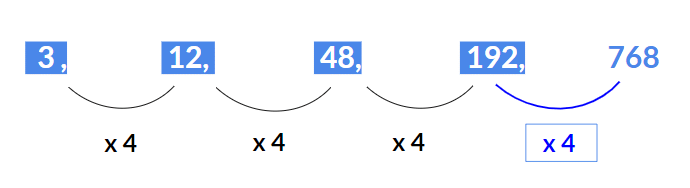
उदाहरण 1: गायब पद ज्ञात करें 3, 12, 48, 192, ? समाधान: यहाँ प्रत्येक संख्या को 4 से गुणा किया जाता है। अर्थात:
- 12 = 3 x 4
- 48 = 12 x 4
- 192 = 48 x 4
अतः अगला पद होगा 192 x 4 = 768।
उदाहरण 2: अगला पद ज्ञात करें 729, 243, 81, 27, ? समाधान: यहाँ प्रत्येक संख्या को 3 से भाग दिया जाता है।
- 729/3 = 243
- 243/3 = 81
- 81/3 = 27
अतः अगला पद होगा 27/3 = 9
प्रकार 12: मिश्रित श्रृंखला
एक श्रृंखला जिसमें एक से अधिक पैटर्न एकल श्रृंखला में व्यवस्थित होते हैं।
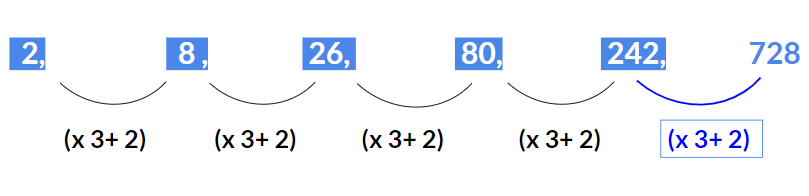
उदाहरण 1: गायब संख्या का पता लगाएं 2, 8, 26, 80, 242, ? समाधान: यहां पैटर्न है (x 3 2)।
- 2 x 3 2 = 8
- 8 x 3 2 = 26
- 26 x 3 2 = 80
- 80 x 3 2 = 242
इसलिए गायब संख्या होगी 242 x 3 2 = 728
उदाहरण 2: अगली संख्या का पता लगाएं 5, 12, 27, 59, ? समाधान: यहां प्रत्येक संख्या को 2 से गुणा किया जाता है और लगातार प्राइम नंबर जोड़े जाते हैं।
- 5 x 2 + 2 = 12
- 12 x 2 + 3 = 27
- 27 x 2 + 5 = 59
इसलिए अगली संख्या होगी 59 x 2 + 7 = 125
प्रकार 13: अंकगणितीय – ज्यामितीय श्रृंखला
एक श्रृंखला जो अंकगणितीय और ज्यामितीय श्रृंखला का संयोजन है।
उदाहरण: अगली संख्या का पता लगाएं 3, 5, 10, 12, 24, 26, ? समाधान: यहां पैटर्न है (2, x 2, 2, x 2 …..)
- 3 + 2 = 5
- 5 x 2 = 10
- 10 + 2 = 12
- 12 x 2 = 24
- 24 + 2 = 26
इसलिए अगली संख्या होगी 26 x 2 = 52
प्रकार 14: वैकल्पिक श्रृंखला
प्रकार 14: वैकल्पिक श्रृंखला
एक श्रृंखला जहाँ दो श्रृंखलाएँ मिलकर एक एकल श्रृंखला बनाती हैं।
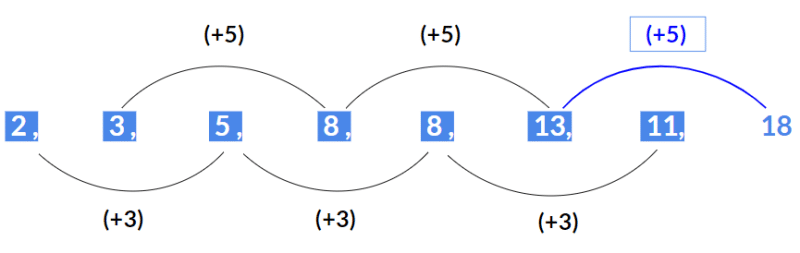
उदाहरण 1: अगला पद खोजें 2, 3, 5, 8, 8, 13, 11, ? समाधान: ► यहाँ वैकल्पिक पद जो 2 से शुरू होते हैं, एक अंकगणितीय श्रृंखला बनाते हैं जिसमें सामान्य अंतर 3 है। (2, 5, 8, 11) ► इसके अतिरिक्त, वैकल्पिक पद जो 3 से शुरू होते हैं, एक और अंकगणितीय श्रृंखला बनाते हैं जिसमें सामान्य अंतर 5 है। (3, 8, 13,..)
इसलिए अगला पद 18 होगा।
उदाहरण 2: अगला पद खोजें 3, 5, 7, 10, 11, 15, 15, ? समाधान: यहाँ वैकल्पिक पद जो 3 से शुरू होते हैं, एक अंकगणितीय श्रृंखला बनाते हैं जिसमें सामान्य अंतर 4 है। (3, 7, 11, 15) इसके अतिरिक्त, वैकल्पिक पद जो 5 से शुरू होते हैं, एक भिन्नात्मक श्रृंखला बनाते हैं जिसमें सामान्य अनुपात 2 है। (5, 10, 15) इसलिए अगला पद 20 होगा।
याद रखने योग्य महत्वपूर्ण बिंदु
- यदि परिवर्तन धीमा या क्रमिक है, तो यह एक अंतर श्रृंखला है।
- उदाहरण:
- यदि परिवर्तन समान रूप से तीव्र है, तो यह अनुपात श्रृंखला है।
- यदि प्रारंभ में वृद्धि तीव्र है, लेकिन बाद में धीमी हो जाती है, तो यह वर्ग या घन संख्याओं को जोड़कर बनाई जाती है।
- यदि श्रृंखला वैकल्पिक है, तो यह मिश्रित श्रृंखला हो सकती है या दो विभिन्न संचालन वैकल्पिक रूप से चल रहे हैं।




|
142 videos|172 docs|185 tests
|















