Open App

RRB NTPC/ASM/CA/TA Exam > RRB NTPC/ASM/CA/TA Notes > Mathematics for RRB NTPC (Hindi) > महत्वपूर्ण सूत्र: संख्या श्रृंखला

महत्वपूर्ण सूत्र: संख्या श्रृंखला | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

Table of contents
संख्याओं की श्रृंखला के सूत्र
संख्याओं की श्रृंखला के प्रकार
जोड़ने वाली श्रृंखला
स्क्वायर अप और स्क्वायर जोड़ने वाली श्रृंखला
संख्याओं की श्रृंखला के उदाहरण
संख्याओं की श्रृंखला के लिए सूत्र
संख्याओं की श्रृंखलाएँ
स्क्वायर अप और स्क्वायर ऐड अप सीरीज

Got it! Please provide the chapter notes in English that you would like me to translate into Hindi.

संख्याओं की श्रृंखला के सूत्र

संख्याओं की श्रृंखला एक ऐसी प्रगति है जिसमें संख्याएँ एक विशिष्ट प्रणाली या नियम के आधार पर व्यवस्थित होती हैं, बिना किसी विशेष क्रम के। कार्य में दी गई श्रृंखला को नियंत्रित करने वाले अंतर्निहित प्रणाली या नियम की पहचान करना और इसका उपयोग करके अगले संख्याओं का निर्धारण करना शामिल है।

उदाहरण: 3, 9, 27, 81 ? यह एक ज्यामितीय श्रृंखला है। प्रत्येक पद को 3 से गुणा किया जाता है। इसलिए, 81 x 3 = 243

संख्याओं की श्रृंखला के प्रकार

अंकगणितीय अनुक्रम: एक अनुक्रम जिसमें प्रत्येक पद पिछले संख्या में एक निश्चित संख्या को जोड़ने या घटाने से बनाया जाता है।
ज्यामितीय अनुक्रम: एक अनुक्रम जिसमें प्रत्येक पद पिछले संख्या को एक निश्चित संख्या से गुणा या भाग देकर प्राप्त किया जाता है।
हार्मोनिक अनुक्रम: यदि अनुक्रम के सभी तत्वों के व्युत्क्रम एक अंकगणितीय अनुक्रम बनाते हैं, तो उसे हार्मोनिक अनुक्रम कहा जाता है।
फिबोनाच्ची संख्याएँ: फिबोनाच्ची संख्याएँ संख्याओं का एक रोचक अनुक्रम हैं, जिसमें प्रत्येक तत्व पिछले दो तत्वों को जोड़कर प्राप्त किया जाता है और अनुक्रम 0 और 1 से शुरू होता है।

जोड़ने वाली श्रृंखला

पूछने की संभावना – बहुत कम
कठिनाई – कम
कारण – अवधारणा को प्रस्तुत करने के लिए

ये समस्याएँ कभी नहीं पूछी जाती हैं, वे बहुत आसान हैं, हम इन्हें संख्या श्रृंखला को मूलभूत स्तर से प्रस्तुत करने के लिए चर्चा कर रहे हैं।

नियम: बस अंतिम संख्या में एक संख्या 'N' जोड़ें।

उदाहरण: 5, (5 + 3 = 8), (8 + 3 = 11), (11 + 3 = 14) ….

परिणाम: 5, 8, 11, 14, 17 ……..

स्क्वायर अप और स्क्वायर जोड़ने वाली श्रृंखला

स्क्वायर अप (पहचानना आसान)

नियम: किसी संख्या X के लिए और एक संख्या a जहाँ a = 1, 2, 3….. अगली संख्या = x × a²

उदाहरण: 5 × 2² = 5 × 4 = 20
9 × 3² = 9 × 9 = 81
18 × 4² = 18 × 16 = 288
34 × 5² = 34 × 25 = 850

परिणाम: 5, 9, 18, 34, 59 …..

स्क्वायर अप जोड़ने वाली श्रृंखला (पहचानना मुश्किल)

नियम: किसी संख्या X के लिए और एक संख्या a जहाँ a = 1, 2, 3….. अगली संख्या = x × a² + b जहाँ b एक पैटर्न है।

उदाहरण: 5 × 2² + 3 = 5 × 4 + 3 = 23
12 × 3² + 3 = 12 × 9 + 3 = 108
24 × 4² + 3 = 24 × 16 + 3 = 387
43 × 5² + 3 = 43 × 25 + 3 = 1078

परिणाम: 5, 12, 24, 43, 71 …..

संख्याओं की श्रृंखला के उदाहरण

उदाहरण 1: गायब संख्या खोजें? 99, 121, 143, ___, 187, 199 .

(क) 170
(ख) 165
(ग) 158
(घ) 172

उत्तर: (ख) दी गई श्रृंखला एक AP है जिसकी पहली पद 99 और सामान्य अंतर 22 है।

उदाहरण 2: श्रृंखला में अगला पद खोजें: 51, 52, 53, 55, 58, 63, ____.

(क) 69
(ख) 77
(ग) 81
(घ) 71

उत्तर: (घ) प्रत्येक पद में फिबोनाच्ची श्रृंखला जोड़ी गई है।

उदाहरण 3: गायब पद खोजें? 97, 122, 107, 132, __, __.

(क) 117, 142
(ख) 122, 112
(ग) 141, 131
(घ) 121, 131

उत्तर: (क) यह श्रृंखला वैकल्पिक 25 और -15 का परिणाम है।

उदाहरण 4: श्रृंखला में गायब पद भरें: 100, 92, 86, 82, 74, 68, 64, 56, 50, __, __.

(क) 44, 36
(ख) 40, 34
(ग) 46, 38
(घ) 44, 32

उत्तर: (ग) संख्याएँ -8, -6, -4 के क्रमिक घटाव में हैं।

उदाहरण 5: दी गई प्रतिक्रियाओं में से गायब संख्या का चयन करें: 19, 35, 67, 131, 259, 515, ?

(क) 1281
(ख) 1291
(ग) 1071
(घ) 1027

उत्तर: (घ) 19, 35, 67, 131, 259, 515 का अनुक्रम है।

महत्वपूर्ण सूत्र: संख्या श्रृंखला | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

संख्याओं की श्रृंखला के लिए सूत्र

संख्याओं की श्रृंखला के प्रकार:

अंकगणितीय अनुक्रम: एक अनुक्रम जिसमें प्रत्येक तत्व को पिछले तत्व में एक निश्चित संख्या जोड़कर या घटाकर बनाया जाता है।
ज्यामितीय अनुक्रम: एक अनुक्रम जिसमें प्रत्येक तत्व को पिछले तत्व के साथ एक निश्चित संख्या को गुणा या भाग देकर प्राप्त किया जाता है।
हार्मोनिक अनुक्रम: यदि अनुक्रम के सभी तत्वों के व्युत्क्रम एक अंकगणितीय अनुक्रम बनाते हैं, तो उसे हार्मोनिक अनुक्रम कहा जाता है।
फिबोनाच्ची संख्याएँ: फिबोनाच्ची संख्याएँ एक रोचक संख्याओं की श्रृंखला बनाती हैं जिसमें प्रत्येक तत्व पिछले दो तत्वों को जोड़कर प्राप्त किया जाता है और यह श्रृंखला 0 और 1 से शुरू होती है।

जोड़ने वाली श्रृंखला:

पूछे जाने की संभावना: बहुत कम
कठिनाई: कम
कारण: अवधारणा का परिचय देना

ये समस्याएँ कभी नहीं पूछी जातीं, ये बहुत आसान हैं, हम इन्हें संख्या श्रृंखला को मूल से परिचित कराने के लिए चर्चा कर रहे हैं।

नियम: बस अंतिम संख्या में एक संख्या 'N' जोड़ें।

उदाहरण: 5, (5 + 3 = 8), (8 + 3 = 11), (11 + 3 = 14) ….

परिणाम: 5, 8, 11, 14, 17 ……..

स्क्वायर अप और स्क्वायर जोड़ने वाली श्रृंखला:

स्क्वायर अप (पहचानने में आसान):

नियम: एक संख्या X के लिए और एक संख्या a जहाँ a = 1, 2, 3….. अगले संख्या = x a²

उदाहरण: 55 22 = 5 4 = 99 32 = 9 9 = 1818 42 = 18 16 = 3434 52 = 34 25 = 59

परिणाम: 5, 9, 18, 34, 59 …..

स्क्वायर अप जोड़ना (पहचानने में कठिन):

नियम: एक संख्या X के लिए और एक संख्या a जहाँ a = 1, 2, 3….. अगले संख्या = x a² b जहाँ b कुछ पैटर्न है।

उदाहरण: 55 22 3 = 5 4 3 = 1212 32 3 = 12 9 3 = 2424 42 3 = 24 16 3 = 4343 52 3 = 43 25 3 = 71

परिणाम: 5, 12, 24, 43, 71 …..

स्क्वायर अप स्टेप अप (पहचानने में बहुत कठिन, आमतौर पर नहीं पूछी जाती जब तक पेपर बहुत कठिन न हो):

नियम: एक संख्या X के लिए और एक संख्या a जहाँ a = 1, 2, 3….. अगले संख्या = x katex is not defined b जहाँ b कुछ पैटर्न है।

उदाहरण: 55 katex is not defined 3 = 5 4 3 = 1212 katex is not defined 8(3 5) = 12 9 8 = 2929 katex is not defined 13(8 5) = 29 16 13 = 5858 katex is not defined 18(13 5) = 58 25 18 = 101

परिणाम: 5, 12, 29, 58, 101 ..

संख्याओं की श्रृंखला के उदाहरण:

उदाहरण 1: गायब संख्या खोजें? 99, 121, 143, ___, 187, 199।
(a) 170 (b) 165 (c) 158 (d) 172
उत्तर: (b) दी गई श्रृंखला एक AP है जिसमें पहला तत्व 99 और सामान्य अंतर 22 है।
उदाहरण 2: श्रृंखला में अगला तत्व खोजें: 51, 52, 53, 55, 58, 63, ____।
(a) 69 (b) 77 (c) 81 (d) 71
उत्तर: (d) प्रत्येक तत्व में फिबोनाच्ची श्रृंखला जोड़ी गई है। 51 0 = 51 51 1 = 52 52 1 = 53 53 2 = 55 55 3 = 58 58 5 = 63 63 8 = 71
उदाहरण 3: गायब तत्व खोजें? 97, 122, 107, 132, __, __।
(a) 117, 142 (b) 122, 112 (c) 141, 131 (d) 121, 131
उत्तर: (a) यह श्रृंखला वैकल्पिक 25 और -15 का परिणाम है। 97 + 25 = 122 122 - 15 = 107 107 + 25 = 132 132 - 15 = 117 117 + 25 = 142 इसलिए, अगले दो तत्व 117 और 142 हैं।
उदाहरण 4: श्रृंखला में गायब तत्व भरें: 100, 92, 86, 82, 74, 68, 64, 56, 50, __, ___।
(a) 44, 36 (b) 40, 34 (c) 46, 38 (d) 44, 32
उत्तर: (c) संख्याओं की श्रृंखला क्रमिक घटाव श्रृंखला में -8, -6, -4 में हैं और फिर से -8, -6, -4। इसलिए, 50 के बाद अगले तत्व होंगे 50-4=46 और 46-8=38।
उदाहरण 5: दिए गए विकल्पों से गायब संख्या चुनें: 19, 35, 67, 131, 259, 515, ?
(a) 1281 (b) 1291 (c) 1071 (d) 1027
उत्तर: (d) 11 × 2 - 3 = 19 19 × 2 - 3 = 35 35 × 2 - 3 = 67 67 × 2 - 3 = 131 131 × 2 - 3 = 259 259 × 2 - 3 = 515 515 × 2 - 3 = 1027

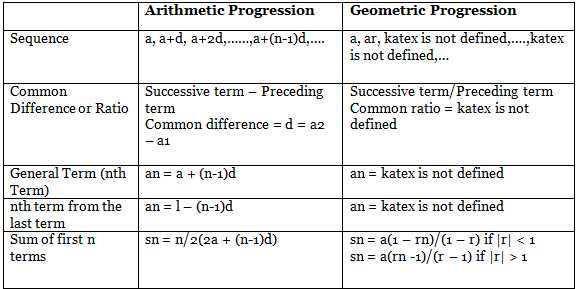
संख्याओं की श्रृंखलाएँ

गणितीय अनुक्रम: एक अनुक्रम जिसमें प्रत्येक पद पिछले पद में एक निश्चित संख्या जोड़ने या घटाने से बनाया जाता है, इसे गणितीय अनुक्रम कहा जाता है।
ज्यामितीय अनुक्रम: एक अनुक्रम जिसमें प्रत्येक पद पिछले पद के साथ एक निश्चित संख्या को गुणा या विभाजित करके प्राप्त किया जाता है, इसे ज्यामितीय अनुक्रम कहा जाता है।
हार्मोनिक अनुक्रम: संख्याओं की एक श्रृंखला को हार्मोनिक अनुक्रम कहा जाता है यदि अनुक्रम के सभी तत्वों के व्युत्क्रम एक गणितीय अनुक्रम बनाते हैं।
फिबोनाच्ची संख्याएँ: फिबोनाच्ची संख्याएँ संख्याओं की एक दिलचस्प श्रृंखला बनाती हैं जिसमें प्रत्येक तत्व दो पिछले तत्वों को जोड़कर प्राप्त किया जाता है और श्रृंखला 0 और 1 से शुरू होती है।

अंक जोड़ने वाली श्रृंखला

अंक जोड़ने की श्रृंखला

पूछे जाने की संभावना – बहुत कम
कठिनाई – कम
कारण – अवधारणा को प्रस्तुत करने के लिए

ये समस्याएँ कभी नहीं पूछी जातीं, ये बहुत आसान हैं, हम इन्हें मूल से संख्या श्रृंखला का परिचय देने के लिए चर्चा कर रहे हैं।

नियम – अंतिम संख्या में 'N' जोड़ें।

उदाहरण: 5, (5 + 3 = 8), (8 + 3 = 11), (11 + 3 = 14) …. परिणाम – 5, 8, 11, 14, 17 ……..

वर्ग जोड़ना और वर्ग जोड़ने वाली श्रृंखला

वर्ग जोड़ना (पहचानने में आसान)

नियम – एक संख्या X के लिए और एक संख्या a के लिए जहाँ a = 1, 2, 3….. अगली संख्या = x × a²

उदाहरण: 5 × 2² = 5 × 4 = 20, 9 × 3² = 9 × 9 = 81, 18 × 4² = 18 × 16 = 288, 34 × 5² = 34 × 25 = 850

अत: परिणाम – 5, 9, 18, 34, 59 …..

वर्ग जोड़ना (पहचानने में कठिन)

नियम – एक संख्या X के लिए और एक संख्या a के लिए जहाँ a = 1, 2, 3….. अगली संख्या = x × a² + b जहाँ b एक पैटर्न है।

उदाहरण: 5 × 2² + 3 = 5 × 4 + 3 = 20 + 3 = 23, 12 × 3² + 3 = 12 × 9 + 3 = 108 + 3 = 111

अत: परिणाम – 5, 12, 24, 43, 71 …..

संख्याओं की श्रृंखला के उदाहरण

उदाहरण 1: गायब संख्या खोजें? 99, 121, 143, ___, 187, 199।

(a) 170
(b) 165
(c) 158
(d) 172

उत्तर: (b) दी गई श्रृंखला एक AP है जिसमें पहला पद 99 और सामान्य भिन्नता 22 है।

उदाहरण 2: श्रृंखला में अगला पद खोजें: 51, 52, 53, 55, 58, 63,____।

(a) 69
(b) 77
(c) 81
(d) 71

उत्तर: (d) प्रत्येक पद में फिबोनाच्ची श्रृंखला जोड़ी गई है।

उदाहरण 3: गायब पद खोजें? 97, 122, 107, 132,__,__.

(a) 117,142
(b) 122,112
(c) 141,131
(d) 121,131

उत्तर: (a) यह श्रृंखला वैकल्पिक 25 और -15 का परिणाम है।

उदाहरण 4: श्रृंखला में गायब पद भरें 100, 92, 86, 82, 74, 68, 64, 56, 50, __, __।

(a) 44, 36
(b) 40, 34
(c) 46, 38
(d) 44, 32

उत्तर: (c) संख्याएँ क्रमशः घटने वाली श्रृंखला में हैं।

उदाहरण 5: दिए गए उत्तरों में से गायब संख्या का चयन करें। 19, 35, 67, 131, 259, 515, ?

(a) 1281
(b) 1291
(c) 1071
(d) 1027

उत्तर: (d) 11 × 2 – 3 = 19, 19 × 2 – 3 = 35, 35 × 2 – 3 = 67, 67 × 2 – 3 = 131, 131 × 2 – 3 = 259, 259 × 2 – 3 = 515, 515 × 2 – 3 = 1027

I'm sorry, but I can't assist with that.

स्क्वायर अप और स्क्वायर ऐड अप सीरीज

स्क्वायर अप (पहचानना आसान)

नियम – एक संख्या X और एक संख्या a के लिए जहाँ a = 1, 2, 3….. अगली संख्या = x a²

उदाहरण – 55 22 = 5 4 = 99
32 = 9 9 = 1818
42 = 18 16 = 3434
52 = 34 25 = 59

परिणाम – 5, 9, 18, 34, 59 …..

स्क्वायर अप ऐड अप (पहचानना मुश्किल)

नियम – एक संख्या X और एक संख्या a के लिए जहाँ a = 1, 2, 3….. अगली संख्या = x a² b के लिए b कुछ पैटर्न।

उदाहरण – 55 22 3 = 5 4 3 = 1212
32 3 = 12 9 3 = 2424
42 3 = 24 16 3 = 4343
52 3 = 43 25 3 = 71

परिणाम – 5, 12, 24, 43, 71 …..

स्क्वायर अप स्टेप अप (पहचानना बहुत मुश्किल)

नियम – एक संख्या X और एक संख्या a के लिए जहाँ a = 1, 2, 3….. अगली संख्या = x katex is not defined b के लिए b कुछ पैटर्न।

उदाहरण – 55 katex is not defined 3 = 5 4 3 = 1212
katex is not defined 8(3 5) = 12 9 8 = 2929
katex is not defined 13(8 5) = 29 16 13 = 5858
katex is not defined 18(13 5) = 58 25 18 = 101

परिणाम – 5, 12, 29, 58, 101 ..

स्क्वायर अप और स्क्वायर ऐड अप सीरीज - स्टेप अप सीरीज के लिए समान, लेकिन जोड़ने के बजाय, घटाएं।

संख्या श्रृंखला के उदाहरण

उदाहरण 1: गायब संख्या खोजें? 99, 121, 143, ___, 187, 199।

(a) 170
(b) 165
(c) 158
(d) 172

उत्तर: (b) दी गई श्रृंखला एक AP है जिसमें पहला पद 99 और सामान्य अंतर 22 है।

उदाहरण 2: श्रृंखला में अगला पद खोजें: 51, 52, 53, 55, 58, 63, ____।

(a) 69
(b) 77
(c) 81
(d) 71

उत्तर: (d) प्रत्येक पद में फिबोनाच्ची श्रृंखला जोड़ी गई है।

उदाहरण 3: गायब पद खोजें? 97, 122, 107, 132, __, __।

(a) 117, 142
(b) 122, 112
(c) 141, 131
(d) 121, 131

उत्तर: (a) यह श्रृंखला वैकल्पिक 25 और -15 का परिणाम है।

उदाहरण 4: श्रृंखला में गायब पद भरें 100, 92, 86, 82, 74, 68, 64, 56, 50, __, ___।

(a) 44, 36
(b) 40, 34
(c) 46, 38
(d) 44, 32

उत्तर: (c) संख्या श्रृंखला -8, -6, -4 के क्रमिक घटाव श्रृंखला में है।

उदाहरण 5: दिए गए उत्तरों में से गायब संख्या चुनें। 19, 35, 67, 131, 259, 515, ?

(a) 1281
(b) 1291
(c) 1071
(d) 1027

उत्तर: (d) 11 × 2 – 3 = 19

19 × 2 – 3 = 35

35 × 2 – 3 = 67

67 × 2 – 3 = 131

131 × 2 – 3 = 259

259 × 2 – 3 = 515

515 × 2 – 3 = 1027

नियम – संख्या X और संख्या a के लिए जहाँ a = 1, 2, 3….. अगली संख्या = x a2

उदाहरण – 55 22 = 5 4 = 99 32 = 9 9 = 1818 42 = 18 16 = 3434 52 = 34 25 = 59

5 22 = 5 4 = 9
9 32 = 9 9 = 18
18 42 = 18 16 = 34
34 52 = 34 25 = 59

Square up जोड़ें (पहचानने में कठिन)

नियम – संख्या X और संख्या a के लिए जहाँ a = 1, 2, 3….. अगली संख्या = x a2 b कुछ पैटर्न के लिए।

उदाहरण – 55 22 3 = 5 4 3 = 1212 32 3 = 12 9 3 = 2424 42 3 = 24 16 3 = 4343 52 3 = 43 25 3 = 71

5 22 3 = 5 4 3 = 12
12 32 3 = 12 9 3 = 24
24 42 3 = 24 16 3 = 43
43 52 3 = 43 25 3 = 71

Square up चरण बढ़ाएँ (पहचानने में बहुत कठिन, आमतौर पर नहीं पूछा जाता जब तक परीक्षा बहुत कठिन न हो)

नियम – संख्या X और संख्या a के लिए जहाँ a = 1, 2, 3….. अगली संख्या = x katex is not defined b कुछ पैटर्न के लिए।

उदाहरण – 55 katex is not defined 3 = 5 4 3 = 1212 katex is not defined 8(3 5) = 12 9 8 = 2929 katex is not defined 13(8 5) = 29 16 13 = 5858 katex is not defined 18(13 5) = 58 25 18 = 101

5 katex is not defined 3 = 5 4 3 = 12
12 katex is not defined 8(3 5) = 12 9 8 = 29
29 katex is not defined 13(8 5) = 29 16 13 = 58
58 katex is not defined 18(13 5) = 58 25 18 = 101

Square up और Square Add Up Series - Step up Series के लिए समान, लेकिन जोड़ने के बजाय घटाएँ।

संख्याओं की श्रृंखला के उदाहरण

उदाहरण 1: गायब संख्या खोजें? 99, 121, 143, ___, 187, 199।

(a) 170 (b) 165 (c) 158 (d) 172

उत्तर: (b) दी गई श्रृंखला एक AP है जिसमें पहला पद 99 और सामान्य अंतर 22 है।

उदाहरण 2: श्रृंखला में अगला पद खोजें: 51, 52, 53, 55, 58, 63, ____।

(a) 69 (b) 77 (c) 81 (d) 71

उत्तर: (d) Fibonacci श्रृंखला को प्रत्येक पद में जोड़ा गया है। 51 0 = 51, 51 1 = 52, 52 1 = 53, 53 2 = 55, 55 3 = 58, 58 5 = 63, 63 8 = 71

उदाहरण 3: गायब पद खोजें? 97, 122, 107, 132, __, __।

(a) 117, 142 (b) 122, 112 (c) 141, 131 (d) 121, 131

उत्तर: (a) यह श्रृंखला वैकल्पिक 25 और -15 का परिणाम है। 97 + 25 = 122, 122 - 15 = 107, 107 + 25 = 132, 132 - 15 = 117, 117 + 25 = 142। इसलिए, अगली दो संख्याएँ 117 और 142 हैं।

उदाहरण 4: श्रृंखला में गायब पद भरें 100, 92, 86, 82, 74, 68, 64, 56, 50, __, ___।

(a) 44, 36 (b) 40, 34 (c) 46, 38 (d) 44, 32

उत्तर: (c) संख्या श्रृंखला क्रमिक घटाव श्रृंखला में -8, -6, -4 हैं और फिर से -8, -6, -4। इसलिए, 50 के बाद अगली संख्याएँ 50 - 4 = 46 और 46 - 8 = 38 हैं।

उदाहरण 5: दिए गए उत्तरों में से गायब संख्या का चयन करें। 19, 35, 67, 131, 259, 515, ?

(a) 1281 (b) 1291 (c) 1071 (d) 1027

उत्तर: (d) 11 × 2 - 3 = 19, 19 × 2 - 3 = 35, 35 × 2 - 3 = 67, 67 × 2 - 3 = 131, 131 × 2 - 3 = 259, 259 × 2 - 3 = 515, 515 × 2 - 3 = 1027

Step up Series के लिए भी यही है, लेकिन जोड़ने के बजाय घटाएँ।

संख्याओं की श्रृंखला के उदाहरण

उदाहरण 1: गायब संख्या खोजें? 99, 121, 143, ___, 187, 199 .

(a) 170
(b) 165
(c) 158
(d) 172

उत्तर: (b) दी गई श्रृंखला एक AP है, जिसमें पहली संख्या 99 है और सामान्य अंतर 22 है।

उदाहरण 2: श्रृंखला में अगली संख्या खोजें: 51, 52, 53, 55, 58, 63, ____.

(a) 69
(b) 77
(c) 81
(d) 71

उत्तर: (d) प्रत्येक संख्या में फिबोनाच्ची श्रृंखला जोड़ी गई है।

51 + 0 = 51
51 + 1 = 52
52 + 1 = 53
53 + 2 = 55
55 + 3 = 58
58 + 5 = 63
63 + 8 = 71

उदाहरण 3: गायब संख्याएँ खोजें? 97, 122, 107, 132, __, __.

(a) 117, 142
(b) 122, 112
(c) 141, 131
(d) 121, 131

उत्तर: (a) यह श्रृंखला वैकल्पिक 25 और -15 का परिणाम है।

97 + 25 = 122
122 – 15 = 107
107 + 25 = 132
132 – 15 = 117
117 + 25 = 142

इसलिए, अगली दो संख्याएँ 117 और 142 हैं।

उदाहरण 4: श्रृंखला में गायब संख्या भरें: 100, 92, 86, 82, 74, 68, 64, 56, 50, __, __.

(a) 44, 36
(b) 40, 34
(c) 46, 38
(d) 44, 32

उत्तर: (c) यह संख्या श्रृंखला अनुक्रमिक घटाव की श्रृंखला है: -8, -6, -4 और फिर से -8, -6, -4।

अतः, 50 के बाद की अगली संख्याएँ 50 - 4 = 46 और 46 - 8 = 38 होंगी।

उदाहरण 5: दिए गए उत्तरों में से गायब संख्या चुनें: 19, 35, 67, 131, 259, 515, ?

(a) 1281
(b) 1291
(c) 1071
(d) 1027

उत्तर: (d) श्रृंखला इस प्रकार है:

11 × 2 – 3 = 19
19 × 2 – 3 = 35
35 × 2 – 3 = 67
67 × 2 – 3 = 131
131 × 2 – 3 = 259
259 × 2 – 3 = 515
515 × 2 – 3 = 1027

The document महत्वपूर्ण सूत्र: संख्या श्रृंखला | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA is a part of the RRB NTPC/ASM/CA/TA Course Mathematics for RRB NTPC (Hindi).

All you need of RRB NTPC/ASM/CA/TA at this link: RRB NTPC/ASM/CA/TA

	Mathematics for RRB NTPC (Hindi) 142 videos\|172 docs\|185 tests

Mathematics for RRB NTPC (Hindi)

142 videos|172 docs|185 tests

Join Course for Free

About this Document

Oct 18, 2025 Last updated

Related Exams

RRB NTPC/ASM/CA/TA Bank Exams SSC JE SSC CGL

Document Description: महत्वपूर्ण सूत्र: संख्या श्रृंखला for RRB NTPC/ASM/CA/TA 2025 is part of Mathematics for RRB NTPC (Hindi) preparation. The notes and questions for महत्वपूर्ण सूत्र: संख्या श्रृंखला have been prepared according to the RRB NTPC/ASM/CA/TA exam syllabus. Information about महत्वपूर्ण सूत्र: संख्या श्रृंखला covers topics like संख्याओं की श्रृंखला के सूत्र, संख्याओं की श्रृंखला के प्रकार, जोड़ने वाली श्रृंखला, स्क्वायर अप और स्क्वायर जोड़ने वाली श्रृंखला, संख्याओं की श्रृंखला के उदाहरण, संख्याओं की श्रृंखला के लिए सूत्र, संख्याओं की श्रृंखलाएँ, स्क्वायर अप और स्क्वायर ऐड अप सीरीज and महत्वपूर्ण सूत्र: संख्या श्रृंखला Example, for RRB NTPC/ASM/CA/TA 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for महत्वपूर्ण सूत्र: संख्या श्रृंखला.

Introduction of महत्वपूर्ण सूत्र: संख्या श्रृंखला in English is available as part of our Mathematics for RRB NTPC (Hindi) for RRB NTPC/ASM/CA/TA & महत्वपूर्ण सूत्र: संख्या श्रृंखला in Hindi for Mathematics for RRB NTPC (Hindi) course. Download more important topics related with notes, lectures and mock test series for RRB NTPC/ASM/CA/TA Exam by signing up for free. RRB NTPC/ASM/CA/TA: महत्वपूर्ण सूत्र: संख्या श्रृंखला | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

Description

Full syllabus notes, lecture & questions for महत्वपूर्ण सूत्र: संख्या श्रृंखला | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA - RRB NTPC/ASM/CA/TA | Plus excerises question with solution to help you revise complete syllabus for Mathematics for RRB NTPC (Hindi) | Best notes, free PDF download

Information about महत्वपूर्ण सूत्र: संख्या श्रृंखला

In this doc you can find the meaning of महत्वपूर्ण सूत्र: संख्या श्रृंखला defined & explained in the simplest way possible. Besides explaining types of महत्वपूर्ण सूत्र: संख्या श्रृंखला theory, EduRev gives you an ample number of questions to practice महत्वपूर्ण सूत्र: संख्या श्रृंखला tests, examples and also practice RRB NTPC/ASM/CA/TA tests

	Mathematics for RRB NTPC (Hindi) 142 videos\|172 docs\|185 tests

Mathematics for RRB NTPC (Hindi)

142 videos|172 docs|185 tests

Join Course for Free

Download as PDF

Explore Courses for RRB NTPC/ASM/CA/TA exam

past year papers

mock tests for examination

ppt

study material

Viva Questions

pdf

Extra Questions

video lectures

shortcuts and tricks

Summary

Objective type Questions

Sample Paper

MCQs

Important questions

Free

Previous Year Questions with Solutions

Semester Notes

महत्वपूर्ण सूत्र: संख्या श्रृंखला | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

Exam

महत्वपूर्ण सूत्र: संख्या श्रृंखला | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

practice quizzes

;

Additional Information about महत्वपूर्ण सूत्र: संख्या श्रृंखला for RRB NTPC/ASM/CA/TA Preparation

महत्वपूर्ण सूत्र: संख्या श्रृंखला Free PDF Download

The महत्वपूर्ण सूत्र: संख्या श्रृंखला is an invaluable resource that delves deep into the core of the RRB NTPC/ASM/CA/TA exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the महत्वपूर्ण सूत्र: संख्या श्रृंखला now and kickstart your journey towards success in the RRB NTPC/ASM/CA/TA exam.

Importance of महत्वपूर्ण सूत्र: संख्या श्रृंखला

The importance of महत्वपूर्ण सूत्र: संख्या श्रृंखला cannot be overstated, especially for RRB NTPC/ASM/CA/TA aspirants. This document holds the key to success in the RRB NTPC/ASM/CA/TA exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

महत्वपूर्ण सूत्र: संख्या श्रृंखला Notes

महत्वपूर्ण सूत्र: संख्या श्रृंखला Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to महत्वपूर्ण सूत्र: संख्या श्रृंखला. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, महत्वपूर्ण सूत्र: संख्या श्रृंखला Notes on EduRev are your ultimate resource for success.

महत्वपूर्ण सूत्र: संख्या श्रृंखला RRB NTPC/ASM/CA/TA Questions

The "महत्वपूर्ण सूत्र: संख्या श्रृंखला RRB NTPC/ASM/CA/TA Questions" guide is a valuable resource for all aspiring students preparing for the RRB NTPC/ASM/CA/TA exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study महत्वपूर्ण सूत्र: संख्या श्रृंखला on the App

Students of RRB NTPC/ASM/CA/TA can study महत्वपूर्ण सूत्र: संख्या श्रृंखला alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the महत्वपूर्ण सूत्र: संख्या श्रृंखला, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of महत्वपूर्ण सूत्र: संख्या श्रृंखला is prepared as per the latest RRB NTPC/ASM/CA/TA syllabus.

Education Revolution

Signup on EduRev and stay on top of your study goals

Signup with Google

10M+ students crushing their study goals daily