महत्वपूर्ण तथ्य और सूत्र: ट्रेनों पर आधारित समस्याएँ | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download
परिचय
ट्रेन से संबंधित मुद्दे 'गति, समय और दूरी' से जुड़े चुनौतियों के समान हैं, और 'गति, समय और दूरी' के कुछ सिद्धांत दोनों पर लागू होते हैं। एकमात्र भिन्नता इन विशेष परिस्थितियों में गतिशील वस्तु (ट्रेन) की लंबाई का समावेश है।

महत्वपूर्ण तथ्य और सूत्र
- किमी/घंटा से मीटर/सेकंड में परिवर्तन:
- मीटर/सेकंड से किमी/घंटा में परिवर्तन:
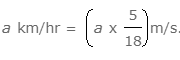
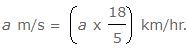
गति, समय और दूरी खोजने के लिए सूत्र
- एक ट्रेन की लंबाई l मीटर है, जो एक खंभे, खड़े व्यक्ति या सिग्नल पोस्ट को पार करने में जो समय लगाती है, वह उस ट्रेन को l मीटर की दूरी तय करने में लगने वाले समय के बराबर है।
- एक ट्रेन की लंबाई l मीटर है, जो एक स्थिर वस्तु की लंबाई b मीटर है, उसे पार करने में जो समय लगता है, वह उस ट्रेन को (l + b) मीटर की दूरी तय करने में लगने वाले समय के बराबर है।
- मान लीजिए कि दो ट्रेनें या दो वस्तुएं एक ही दिशा में u मीटर/सेकंड और v मीटर/सेकंड की गति से चल रही हैं, जहाँ u > v है, तो उनकी सापेक्ष गति = (u - v) मीटर/सेकंड है।
- मान लीजिए कि दो ट्रेनें या दो वस्तुएं विपरीत दिशाओं में u मीटर/सेकंड और v मीटर/सेकंड की गति से चल रही हैं, तो उनकी सापेक्ष गति = (u + v) मीटर/सेकंड है।
- यदि दो ट्रेनें लंबाई a मीटर और b मीटर की हैं और विपरीत दिशाओं में u मीटर/सेकंड और v मीटर/सेकंड की गति से चल रही हैं, तो:
- उन ट्रेनों के एक-दूसरे को पार करने में लगने वाला समय: यदि दो ट्रेनें लंबाई a मीटर और b मीटर की हैं और समान दिशा में u मीटर/सेकंड और v मीटर/सेकंड की गति से चल रही हैं, तो:
- तेज ट्रेन द्वारा धीमी ट्रेन को पार करने में लगने वाला समय: यदि दो ट्रेनें (या वस्तुएं) एक ही समय में A और B से एक-दूसरे के प्रति चलना शुरू करती हैं और पार करने के बाद उन्हें B और A तक पहुँचने में क्रमशः a और b सेकंड लगते हैं, तो:
- (A की गति) : (B की गति) = (√b : √a)
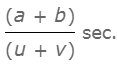
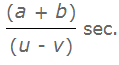
हल करने के नियम
नियम 1
ट्रेन की गति की गणना निम्नलिखित फॉर्मूले का उपयोग करके की जाती है:
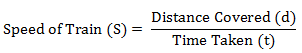
उदाहरण: मान लीजिए कि एक ट्रेन 3 घंटे में 150 किलोमीटर की दूरी तय करती है। हम ट्रेन की गति ज्ञात करने के लिए इस फॉर्मूले का उपयोग कर सकते हैं।
फॉर्मूले का उपयोग करते हुए ट्रेन की गति (S) = तय की गई दूरी (d) / लिया गया समय (t)
जहां तय की गई दूरी (d) 150 किलोमीटर है और लिया गया समय (t) 3 घंटे है, ट्रेन की गति (S) को 50 किलोमीटर प्रति घंटे के रूप में गणना की जाती है, अर्थात् 150/3।
नियम 2
- एक स्थिर वस्तु और गतिशील वस्तु की सापेक्ष गति = गतिशील वस्तु की गति।
- विपरीत दिशा में चलने वाली दो वस्तुओं की सापेक्ष गति = उनकी गति का योग।
- एक ही दिशा में चलने वाली दो वस्तुओं की सापेक्ष गति = उनकी गति का अंतर।
नियम 3
- एक खंभे, स्थिर व्यक्ति, या संकेतक या किसी अन्य नगण्य लंबाई की वस्तु को पार करते समय ट्रेन द्वारा तय की गई दूरी = ट्रेन की लंबाई।
- एक स्थिर वस्तु (पुल, प्लेटफार्म आदि) को पार करते समय ट्रेन द्वारा तय की गई दूरी, जिसकी लंबाई समान है = ट्रेन और उस विशेष स्थिर वस्तु की लंबाई का योग।
नियम 4
नियम 4
- यदि लंबाई a और b की दो ट्रेनें विपरीत दिशा में गति u और v से चल रही हैं, तो एक-दूसरे को पार करने में लगने वाला समय = (a + b) / (u + v).
- यदि लंबाई a और b की दो ट्रेनें समान दिशा में गति u और v से चल रही हैं, तो धीमी ट्रेन को पार करने में तेज ट्रेन द्वारा लगने वाला समय = (a + b) / (v - u).
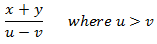
प्रश्नों को हल करने के लिए सुझाव
सुझाव 1
- 1. एक लंबाई L की ट्रेन द्वारा एक खंभे, खड़े व्यक्ति या संकेत पोस्ट को पार करने में लगा समय समान है ट्रेन द्वारा दूरी L को कवर करने में लगे समय के।
- 2. एक लंबाई L की ट्रेन द्वारा एक b लंबाई के स्टेशन को पार करने में लगा समय ट्रेन द्वारा दूरी (L + b) को कवर करने में लगे समय के बराबर है।
उदाहरण 1: एक ट्रेन जो 60 किमी/घंटा की गति से चल रही है, 9 सेकंड में एक खंभे को पार करती है। ट्रेन की लंबाई क्या है? हल: खंभे को पार करने में लगा समय = अपनी लंबाई के बराबर दूरी को कवर करने में लगा समय। ट्रेन की गति को मीटर/सेकंड में परिवर्तित करते हैं = 60 x 5 / 18 = (50/3) मीटर/सेकंड। ट्रेन की लंबाई = ट्रेन की गति x खंभे को पार करने में लगा समय = 50/3 x 9 = ट्रेन की लंबाई = 150 मीटर।
उदाहरण 2: एक ट्रेन 36 सेकंड में एक स्टेशन के प्लेटफॉर्म को पार करती है और 20 सेकंड में प्लेटफॉर्म पर खड़े व्यक्ति को। यदि ट्रेन की गति 54 किमी/घंटा है, तो प्लेटफॉर्म की लंबाई क्या है? हल: ट्रेन की गति को मीटर/सेकंड में = 54 x 5 / 18 = 15 मीटर/सेकंड। ट्रेन की लंबाई = 15 x 20 = 300 मीटर। 36 सेकंड में तय की गई दूरी = 15 x 36 = 540 मीटर। (यह ट्रेन और प्लेटफॉर्म की संयुक्त लंबाई है) प्लेटफॉर्म की लंबाई = (540 – 300) मीटर = 240 मीटर।
सुझाव 2
- 1. यदि लंबाई a और b की दो ट्रेनें विपरीत दिशा में गति u मीटर/सेकंड और v मीटर/सेकंड से चल रही हैं, तो एक-दूसरे को पार करने में लगने वाला समय = (a + b) / (u + v)।
2. यदि दो ट्रेनें जिनकी लंबाई a और b है, समान दिशा में क्रमशः u मीटर/सेकंड और v मीटर/सेकंड की गति से चल रही हैं, तो तेज ट्रेन द्वारा धीमी ट्रेन को पार करने में लगा समय = (a + b) / (u - v) होगा।
उदाहरण 1: 137 मीटर और 163 मीटर लंबाई की 2 ट्रेनें एक-दूसरे की ओर चल रही हैं और उनकी गति क्रमशः 42 किमी/घंटा और 48 किमी/घंटा है। दोनों ट्रेनें एक-दूसरे को पार करने में कितना समय लेंगी? हल: सापेक्ष गति = 42 + 48 = 90 किमी/घंटा = (90 x 5/18) मीटर/सेकंड = 25 मीटर/सेकंड। (विपरीत दिशाएँ) एक-दूसरे को पार करने का समय = 300 / 25 = 12 सेकंड।
उदाहरण 2: 2 ट्रेनें विपरीत दिशाओं में एक आदमी को प्लेटफार्म पर क्रमशः 27 सेकंड और 17 सेकंड में पार करती हैं और वे एक-दूसरे को 23 सेकंड में पार करती हैं। उनकी गति का अनुपात ज्ञात करें। हल: मान लीजिए कि गति क्रमशः x मीटर/सेकंड और y मीटर/सेकंड है। तब, पहली ट्रेन की लंबाई = 27x और दूसरी ट्रेन की लंबाई = 17y। एक-दूसरे को पार करने का समय = (27x + 17y) / (x + y) = 23। = 27x + 17y = 23x + 23y। = 4x = 6y। = x: y = 3 : 2।
टिप 3
उदाहरण: बिना रुकावट के ट्रेन की गति 54 किमी/घंटा है और रुकावट के साथ, यह 45 किमी/घंटा है। ट्रेन प्रति घंटे कितने मिनट रुकती है?
हल:
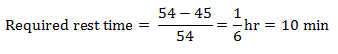
टिप 4
यदि दो ट्रेनें समान लंबाई की हैं और विभिन्न गति से एक पोल को पार करने में समय t1 और t2 लेती हैं, तो एक-दूसरे को पार करने में लगा समय ज्ञात करने की प्रक्रिया:
I. यदि ट्रेनें विपरीत दिशा में चल रही हैं:
II. यदि ट्रेनें समान दिशा में चल रही हैं:
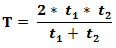
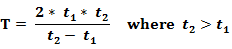
उदाहरण: - दो समान लंबाई की ट्रेनें 4 सेकंड और 5 सेकंड में क्रमशः एक पोल को पार करती हैं। यदि ये ट्रेनें समान दिशा में चल रही हैं, तो वे एक-दूसरे को पार करने में कितना समय लेंगी?
विविध प्रश्न
विविध प्रश्न
1. एक ट्रेन जिसकी लंबाई 300 मीटर है, 54 किमी/घंटा की गति से चल रही है। यह 150 मीटर लंबे पुल को पार करने में कितना समय लेगी?
समाधान:
गति = {54 × (5/18)} मीटर/सेकंड = 15 मीटर/सेकंड
कुल दूरी जो तय करनी है = (300 + 150) मीटर = 450 मीटर
समय = दूरी/गति
आवश्यक समय = 450 / 15 = 30 सेकंड
2. दो ट्रेनों को विपरीत दिशाओं में चलने के लिए एक व्यक्ति को प्लेटफॉर्म पर पार करने में क्रमशः 28 सेकंड और 18 सेकंड लगते हैं। ट्रेनों को एक-दूसरे को पार करने में 26 सेकंड लगे। उनकी गति का अनुपात क्या है?
समाधान:
मान लीजिए पहली ट्रेन की गति x है और दूसरी ट्रेन की गति y है
पहली ट्रेन की लंबाई = गति × समय = 28x
दूसरी ट्रेन की लंबाई = गति × समय = 18y
तो, {(28x + 18y) / (x + y)} = 26
⇒ 28x + 18y = 26x + 26y
⇒ 2x = 8y
इसलिए, x:y = 4:1
3. एक ट्रेन जो 56 किमी/घंटा की गति से चल रही है, 18 सेकंड में एक खंभे को पार करती है। ट्रेन की लंबाई क्या है?
गति = {56 × (5/18)} मीटर/सेकंड = (140/9) मीटर/सेकंड
ट्रेन की लंबाई (दूरी) = गति × समय = {(140/9) × 18} = 280 मीटर
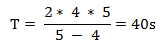
|
142 videos|172 docs|185 tests
|





















