महत्वपूर्ण सूत्र: घड़ी और कैलेंडर | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

प्रतियोगी परीक्षाओं में घड़ी और कैलेंडर से संबंधित प्रश्नों की संख्या विशेष परीक्षा और उसके ढांचे के आधार पर बहुत भिन्न हो सकती है। सामान्यतः, ये विषय तर्कशक्ति या मात्रात्मक खंड का एक छोटा हिस्सा बनाते हैं, जिसमें एक मानक सेट में संभवतः 1-5 प्रश्न हो सकते हैं, हालांकि यह निश्चित नहीं है और प्रत्येक परीक्षा के प्रारूप के साथ बदल सकता है।

घड़ी

• मिनट स्थान: घड़ी का चेहरा या डायल एक गोलाकार सतह है जिसे 60 समान भागों में बांटा गया है, जिसे मिनट स्थान कहा जाता है।
• घंटे की सुई और मिनट की सुई: घड़ी पर छोटी सुई को घंटे की सुई या शॉर्टहैंड कहा जाता है, जबकि बड़ी सुई (एक के बजाय) को मिनट की सुई या लॉन्ग हैंड कहा जाता है।

कैलेंडर

सामान्य और लीप वर्ष

• सामान्य वर्ष: एक सामान्य वर्ष, जो लीप वर्ष नहीं है, में 365 दिन होते हैं।
• लीप वर्ष: एक लीप वर्ष में 366 दिन होते हैं, और यह दो शर्तों का पालन करता है: (a) हर वर्ष जो 4 से विभाजित होता है, वह लीप वर्ष होता है, सिवाय शताब्दियों के। (b) हर 4वीं शताब्दी एक लीप वर्ष होती है, जबकि अन्य शताब्दियों को लीप वर्ष नहीं माना जाता।

अजीब दिन

किसी दिए गए तिथि के सप्ताह के दिन का निर्धारण करते समय, हम 'अजीब दिन' की अवधारणा का उपयोग करते हैं। किसी दिए गए समयावधि में, पूर्ण सप्ताहों के बाद के दिन को अजीब दिन कहा जाता है।

घड़ी के महत्वपूर्ण अवलोकन और सूत्र

घड़ी के महत्वपूर्ण अवलोकन और सूत्र

• एक घड़ी एक पूर्ण वृत्त है जिसमें 360 डिग्री होते हैं। इसे 12 समान भागों में विभाजित किया जाता है, अर्थात् प्रत्येक भाग: 360/12 = 30 डिग्री
• चूंकि मिनट की सुई एक घंटे में एक पूर्ण चक्कर लगाती है, यह 60 मिनट में 360 डिग्री कवर करती है।
• इसके अलावा, चूंकि घंटे की सुई एक घंटे में 12 भागों में से केवल एक भाग कवर करती है, इसका अर्थ है कि घंटे की सुई 60 मिनट में 30 डिग्री कवर करती है, अर्थात् 1/2 डिग्री प्रति मिनट।
• इसलिए, मिनट की सुई की सापेक्ष गति है।
• प्रत्येक घंटे में, दोनों सुइयाँ एक बार मेल खाती हैं। 12 घंटे में, वे 11 बार मिलेंगी। यह केवल 12 और 1 बजे के बीच एक ऐसे घटना के कारण होता है।
• जब सुइयाँ एक-दूसरे के साथ मेल खाती हैं या विपरीत दिशा में होती हैं, तो वे एक ही सीधी रेखा में होती हैं।
• जब दोनों सुइयाँ 90 डिग्री पर होती हैं, तो वे 15 मिनट के अंतर पर होती हैं।
• एक घंटे में, वे दो 90 डिग्री कोण बनाएंगे और 12 घंटे में केवल 22 90 डिग्री कोण होते हैं। यह 3 बजे और 9 बजे पर मिनट और घंटे की सुई द्वारा बनाए गए 90 डिग्री कोण के कारण होता है।
• जब सुइयाँ विपरीत दिशाओं में होती हैं, तो वे 30 मिनट के अंतर पर होती हैं।
• यदि एक घड़ी 9:15 दिखाती है, जबकि सही समय 9 है, तो इसे 15 मिनट जल्दी कहा जाता है। दूसरी ओर, यदि यह 8:45 दिखाती है, जबकि सही समय 9 है, तो इसे 15 मिनट देर से कहा जाता है।
• यदि दोनों घंटे और मिनट की सुई अपनी सामान्य गति से चलती हैं, तो दोनों सुइयाँ 22 बार एक दिन में मिलेंगी।
• एक दिन में, घड़ी की सुइयाँ एक सीधी रेखा में लेकिन विपरीत दिशा में 44 बार होती हैं।
• एक दिन में, घड़ी की सुइयाँ 44 बार 90 डिग्री पर होती हैं।
• एक दिन में, घड़ी की सुइयाँ 22 बार मेल खाती हैं।

घड़ी का सूत्र 1:

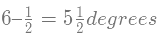
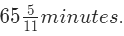
यदि मिनट की सुई घंटे की सुई से पीछे है, तो H बजे M मिनट पर दोनों सुइयों के बीच का कोण निम्नलिखित सूत्र का उपयोग करके गणना की जा सकती है:

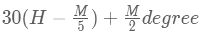
घड़ियों का सूत्र 2:

यदि मिनट की सुई घंटे की सुई से आगे है, तो H बजे M मिनट पर दोनों सुइयों के बीच का कोण निम्नलिखित सूत्र का उपयोग करके निर्धारित किया जा सकता है:

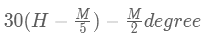
कैलेंडर के लिए महत्वपूर्ण अवलोकन और सूत्र

• एक लीप वर्ष में 366 दिन होते हैं।
• हर वर्ष जो 4 से विभाज्य है, वह एक लीप वर्ष है, यदि वह शताब्दी नहीं है।
• हर 4वीं शताब्दी एक लीप वर्ष है और कोई अन्य शताब्दी लीप वर्ष नहीं है।
• अजीब दिनों की गणना: 1 सामान्य वर्ष ≡ 365 दिन ≡ (52 सप्ताह 1 दिन) इसलिए 1 सामान्य वर्ष में अजीब दिनों की संख्या = 1।
• 1 लीप वर्ष = 366 दिन = (52 सप्ताह 2 दिन) इसलिए 1 लीप वर्ष में अजीब दिनों की संख्या = 2।
• 100 वर्ष = (76 सामान्य वर्ष 24 लीप वर्ष) = (76 x 1 + 24 x 2) अजीब दिन = 124 अजीब दिन। = (17 सप्ताह 5 दिन) = 5 अजीब दिन। इसलिए 100 वर्षों में अजीब दिनों की संख्या = 5।
• 200 वर्षों में अजीब दिनों की संख्या = (5 x 2) = 10 = 3 अजीब दिन।

नमूना घड़ी और कैलेंडर प्रश्नों के साथ समाधान

प्रश्न 1: यदि आपका जन्मदिन सितंबर 2023 के तीसरे सोमवार को पड़ता है, तो आपका जन्मदिन 2027 में किस तारीख को पड़ेगा? हल: 2023 में, 1 सितंबर शुक्रवार है। सितंबर का तीसरा सोमवार 14 दिनों (2 सप्ताह) बाद आता है। 2027 में, 1 सितंबर बुधवार होगा (क्योंकि हर साल दिन 2 दिन आगे बढ़ते हैं)। बुधवार में 14 दिन (2 सप्ताह) जोड़ने पर हमें मिलता है: बुधवार + 14 = गुरुवार। इसलिए, आपका जन्मदिन 2027 में एक गुरुवार को पड़ेगा।

प्रश्न 2: सारा ने अपनी घड़ी को दोपहर 3 बजे सेट किया। जब घड़ी रात 8 बजे दिखाएगी, तो घड़ी की घंटे की सुई कितने डिग्री घूमेगी? हल: दोपहर 3 बजे से रात 8 बजे तक कुल 5 घंटे होते हैं। मानक घड़ी में, घंटे की सुई 12 घंटों में 360° पूरा करती है। अतः 1 घंटे में यह 360° / 12 घंटे = 30° प्रति घंटे चलती है। अब, 5 घंटों के लिए: घंटे की सुई द्वारा घुमाए गए डिग्री = 5 घंटे × 30° प्रति घंटे = 150°। इसलिए, घंटे की सुई दोपहर 3 बजे से रात 8 बजे तक 150° घूमेगी।

प्रश्न 3: उस वर्ष का निर्धारण करें जब कैलेंडर 2015 के वर्ष के समान बिल्कुल पुनरावृत्त होगा। हल: 2015 एक सामान्य वर्ष है। समान कैलेंडर वाले वर्ष को खोजने के लिए, हमें 2015 के 11 वर्ष बाद के वर्ष की तलाश करनी होगी। 2015 + 11 = 2026। इसलिए, वर्ष 2026 का कैलेंडर वर्ष 2015 के कैलेंडर के समान होगा।

प्रश्न 4: थॉमस मिलर, एक जिज्ञासु व्यक्ति, अपने गणित शिक्षक से पूछता है कि उस महीने का 1 तारीख किस दिन पड़ेगा, यदि महीने की 9 तारीख रविवार से पहले वाले दिन पड़ती है। हल: जब महीने की 9 तारीख रविवार से पहले वाले दिन होती है, तो यह स्थापित होता है कि महीने की 8 तारीख शनिवार है। समान महीने की 1 तारीख कब आएगी, यह जानने के लिए हम निम्नलिखित क्रम के साथ आगे बढ़ते हैं:

शनिवार (8)

रविवार (9)

सोमवार (10)

मंगलवार (11)

बुधवार (12)

गुरुवार (13)

शुक्रवार (14)

इसलिए, यदि महीने का 9वां दिन रविवार से ठीक पहले आता है, तो उसी महीने का 1वां दिन शुक्रवार होगा।

प्रश्न 5: हैरी और रोनाल्ड के बीच एक शर्त लगाई गई, जिसमें यह निर्धारित किया गया कि एक कूद वर्ष (leap year) में 53 शुक्रवार (Fridays) होने की संभावना कितनी है। समाधान: 2/7 एक कूद वर्ष में 366 दिन होते हैं, जिसका अर्थ है 52 सप्ताह और 2 दिन। इसलिए, हमारे पास पहले से ही 52 शुक्रवार हैं। अब बाकी के दो दिन हो सकते हैं:

• (रविवार, सोमवार)
• (सोमवार, मंगलवार)
• (मंगलवार, बुधवार)
• (बुधवार, गुरुवार)
• (गुरुवार, शुक्रवार)
• (शुक्रवार, शनिवार)
• (शनिवार, रविवार)

तो, 53 शुक्रवार होने की संभावना = 2/7