समाधान किए गए उदाहरण: त्रिकोण | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

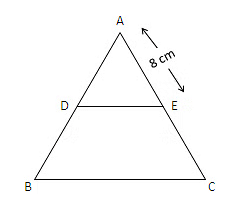
प्रश्न 1: एक △ ABC में, D और E AB और AC भुजाओं पर दो बिंदु हैं, इस प्रकार DE BC के समानांतर है और AD : DB = 2 : 1 है। यदि AE = 8 सेमी है, तो AC की लंबाई ज्ञात करें।

• a) 12 सेमी
• b) 10 सेमी
• c) 16 सेमी
• d) 20 सेमी

उत्तर (A)

यहाँ, AE = 8 सेमी

यहाँ, AC = AE + EC = 4 + 8 = 12 सेमी

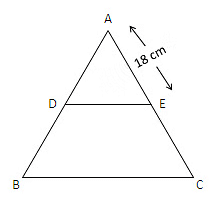
प्रश्न 2: एक △ ABC में, D और E AB और AC भुजाओं पर ऐसे बिंदु हैं कि DE BC के समानांतर है और AD : DB = 3 : 1 है और AE = 18 सेमी। तब AC ज्ञात करें।

• a) 26 सेमी
• b) 24 सेमी
• c) 28 सेमी
• d) 32 सेमी

उत्तर (B)

दिया गया है, DE BC के समानांतर है। तब

यहाँ, AE = 18 सेमी

⇒ EC = 6 सेमी AC = AE + EC = 6 + 18 = 24 सेमी

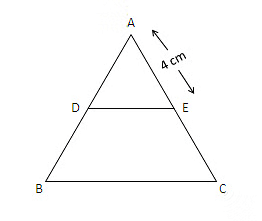
प्रश्न 3: एक △ ABC में, D और E क्रमशः AB और AC भुजाओं पर ऐसे बिंदु हैं कि DE BC के समानांतर है और AD : AB = 2 : 5 और AE = 4 सेमी। तब AC ज्ञात करें।

• a) 10 सेमी
• b) 14 सेमी
• c) 12 सेमी
• d) 9 सेमी

दिया गया है, DE BC के समानांतर है। तब,

AE = 4 सेमी

⇒ EC = 10 सेमी AC = AE + EC = 4 + 10 = 14 सेमी

प्रश्न 4: एक समकोण त्रिकोण के शीर्षों के निर्देशांक A (6, 2), B(8, 0) और C (2, -2) हैं। त्रिकोण PQR के ऑर्थो सेंटर के निर्देशांक हैं:

• a) (2, -2)
• b) (2, 1)
• c) (6, 2)
• d) (8, 0)

उत्तर (C) दिया गया है कि समकोण त्रिकोण के निर्देशांक A (6, 2), B(8, 0) और C (2, -2) हैं। हमें पता है कि दो बिंदुओं (a, b) और (c, d) के बीच की दूरी

इसलिए, कोण A समकोण है। चूंकि यह एक समकोण त्रिकोण है, समकोण के निकट दो भुजाएँ ऊँचाई होंगी। तीसरी ऊँचाई उस शीर्ष पर मिलेगी जहाँ ये दो भुजाएँ मिलती हैं। इसलिए, वह शीर्ष जिसमें समकोण है, ऑर्थो सेंटर है। दिए गए बिंदुओं से, हम स्पष्ट रूप से देख सकते हैं कि (6, 2) ऑर्थो सेंटर है। विकल्प C सही उत्तर है।

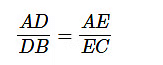
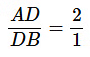
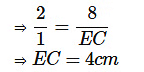
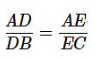
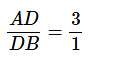
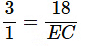
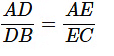
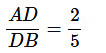
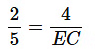
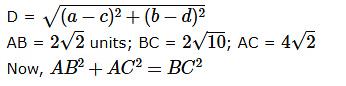
प्रश्न 5: यदि एक समबाहु त्रिकोण की ऊँचाई 24 सेमी है, तो त्रिकोण का क्षेत्रफल ज्ञात करें।

• a)
• b)
• c)
• d)

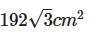
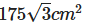
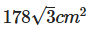
उत्तर (A): दी गई जानकारी के अनुसार, AD = 24 सेमी और ABC एक समबाहु त्रिकोण है। एक समबाहु त्रिकोण में सभी कोण 60° के बराबर होते हैं।

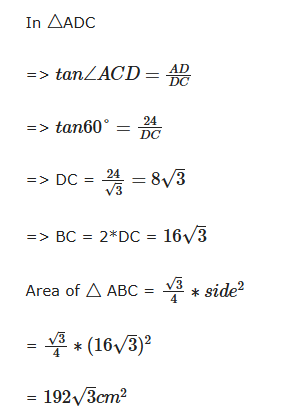
प्रश्न 6: एक त्रिकोणीय मैदान की तीन भुजाएँ क्रमशः 28 मीटर, 45 मीटर और 53 मीटर लंबी हैं। 12 रुपये प्रति वर्ग मीटर के दर से, मैदान में बीज बोने की लागत ज्ञात करें (रु. प्रति वर्ग मीटर)।

• a) 7560
• b) 6860
• c) 7960
• d) 7860

उत्तर (A): दी गई भुजाएँ 28 मीटर, 45 मीटर और 53 मीटर हैं। चूंकि,

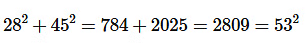
=> दिए गए भुजाएँ एक समकोण त्रिकोण की हैं क्योंकि,

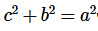
जहाँ a, b, c त्रिकोण की भुजाएँ हैं।

=> त्रिकोणीय क्षेत्र का क्षेत्रफल

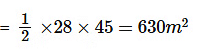
=> बीज बोने की लागत =

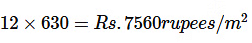
प्रश्न 7: त्रिकोण PQR में, आंतरिक कोण बिसेक्टर ∠𝑄 और ∠𝑅 एक बिंदु O पर इंटरसेक्ट होते हैं। यदि ∠𝑃=110∘ है, तो ∠𝑄𝑂𝑅 का मान क्या है?

• a) 125∘
• b) 135∘
• c) 145∘
• d) 115∘

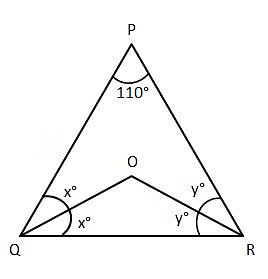
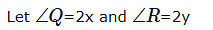
त्रिकोण में कोणों का योग = 180

2x + 2y + 110 = 180

2x + 2y = 70

x + y = 35

इसी तरह त्रिकोण QOR में हमारे पास है

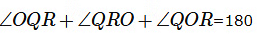
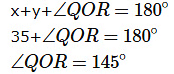
प्रश्न 8: त्रिकोण XYZ में, XA YZ पर कोण बिसेक्टर है। यदि त्रिकोण का अर्धपरिमाप 12 है और XY=12, YZ=6 है, तो YA:AZ का अनुपात क्या है?

• a) 2:3
• b) 2:1
• c) 1:2
• d) 3:2

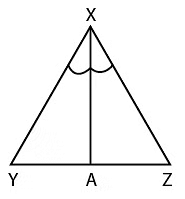
त्रिकोण XYZ में, हमें s=12 है। (x + y + z)/2 = 12

x + y + z = 24

12 + 6 + y = 24

y = 24 - 18

y = 6

कोण बिसेक्टर विपरीत भुजा को अन्य भुजाओं के अनुपात में विभाजित करता है अर्थात् XY/XZ = YA/AZ

YA/AZ = 12/6

YA/AZ = 2:1

प्रश्न 9: त्रिकोण ABC में, AX BC पर कोण बिसेक्टर है। यदि त्रिकोण का अर्धपरिमाप 9 है और AB=4, BC=6 है, तो BX:XC का अनुपात क्या है?

क) 2:3
ख) 2:1
ग) 1:2
घ) 3:2

उत्तर (ग)

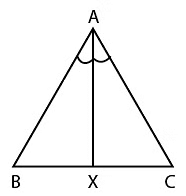
त्रिभुज ABC में हमारे पास s=9 है (a b c)/2 =9
a b c=18 4 6
b=18
b=8 कोण बिसेक्टर विपरीत पक्ष को अन्य पक्षों के अनुपात में विभाजित करता है, अर्थात् AB/AC=BX/XC
BX/XC=4/8
BX/XC=1:2

प्रश्न 10: एक समबाहु त्रिभुज में, यदि h-R=15 सेमी है जहाँ h=त्रिभुज की ऊँचाई और R=परिक्रमण त्रिज्या है, तो त्रिभुज का क्षेत्रफल क्या होगा?

क)
ख)
ग)
घ)

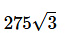
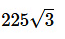
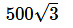
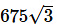
उत्तर (घ)

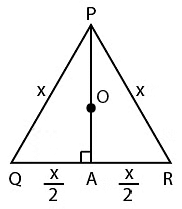
एक समबाहु त्रिभुज में, सभी बिंदु जैसे ओर्थोसेंटर, सेंट्रॉइड, सर्कमसेंटर एक ही स्थान पर होते हैं। मान लें कि त्रिभुज PQR है और परिक्रमण केंद्र O है। मान लें कि मीडियन QR को A पर काटता है। सेंट्रॉइड मीडियन को 2:1 के अनुपात में विभाजित करता है। PA=h, OA=R, OA=15 सेमी। इसलिए (PO:OA)=2:1
PO:15=2:1
PO=30
PA=PO
OP PA=30
15 PA=45
PA भी ऊँचाई है इसलिए इसका उपयोग करके त्रिभुज का पक्ष निकाला जा सकता है।