Explore Exams
Login Signup
Sign in Open App
RRB NTPC/ASM/CA/TA Exam  >  RRB NTPC/ASM/CA/TA Notes  >  Mathematics for RRB NTPC (Hindi)  >  संक्षेप: वृत्त

संक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

Table of contents
सेक्टर सेगमेंट → क्षेत्रफल का सेगमेंट = क्षेत्रफल का सेक्टर OACB – क्षेत्रफल का ∆OAB → परिमाप = आर्क ACB की लंबाई चॉर्ड की लंबाई AB Q1. एक वृत्त के सेगमेंट का क्षेत्रफल ज्ञात करें जिसमें केंद्रीय कोण 120 डिग्री और त्रिज्या 8 सेमी है। हल: क्षेत्रफल का सेगमेंट = 83.047 Q2. एक सेक्टर का क्षेत्रफल ज्ञात करें जिसमें आर्क की लंबाई 30 सेमी और त्रिज्या 10 सेमी है। हल: आर्क की लंबाई = सेक्टर का क्षेत्रफल OAB = Q3. एक वृत्त की त्रिज्या 21 सेमी है और आर्क केंद्र पर 72 डिग्री का कोण बनाता है। आर्क की लंबाई क्या है? हल: आर्क की लंबाई = वृत्त के महत्वपूर्ण गुण - वृत्त के केंद्र से एक चॉर्ड पर खींची गई लंबवत रेखा चॉर्ड को आधा करती है। AM = MB Q1. AB = 8 सेमी और CD = 6 सेमी दो समानांतर चॉर्ड हैं जो वृत्त के केंद्र के एक ही तरफ हैं। उनके बीच की दूरी 1 सेमी है। त्रिज्या की लंबाई ज्ञात करें। हल: ON = x, AO = r त्रिकोण AOE में r² = 16 (x-1)² त्रिकोण OCN में r² = 9 x² 16 (x-1)² = 9 x² x = 4, r² = 9, r = 5 सेमी - समान आर्क के लिए चॉर्ड समान होते हैं। यदि AB = CD, तो ∠1 = ∠2 - वृत्त के समान चॉर्ड केंद्र से समान दूरी पर होते हैं। यदि AB = CD, तो OX = OY - वृत्त के केंद्र पर आर्क द्वारा बनाया गया कोण उस आर्क द्वारा वृत्त के शेष भाग के किसी भी बिंदु पर बनाये गए कोण का दो गुना होता है। x = 2y Q1. एक वृत्त की चॉर्ड की लंबाई उसके त्रिज्या के बराबर है। इस चॉर्ड द्वारा बड़ा सेगमेंट में जो कोण बनता है वो क्या है? हल: OA = OB = r AB त्रिज्या के समान है अतः त्रिकोण OAB एक समद्विबाहु त्रिकोण है कोण OAB = 60° कोण ACB, जो चॉर्ड बनाता है बड़ा कोण = - वृत्त के समान सेगमेंट में कोण समान होते हैं। - अर्धवृत्त में हमेशा दाएं कोण होता है। Q1. AC त्रिकोण ABC का व्यास है। चॉर्ड ED व्यास AC के समानांतर है। यदि कोण CBE = 50°, तो कोण DEC का माप क्या होगा? कोण CBE = 50° कोण ABC = 90° (अर्धवृत्त में कोण हमेशा दाएं होता है) कोण ABE = 90° - 50° = 40° कोण ABE = कोण ACE = 40° कोण ACE = कोण CED = 40° (वैकल्पिक कोण) यदि ABCD एक चक्रीय चतुर्भुज है: - वृत्त के किसी बिंदु पर एक स्पर्श रेखा उस बिंदु पर त्रिज्या के प्रति लंबवत होती है। OP⊥AB - PA × PB = PC × PD - PA × PB = PC × PD Q1. वृत्त के चॉर्ड AB और CD की बाहरी रूप से P पर प्रतिच्छेदन होता है। यदि AB = 6 सेमी, CD = 3 सेमी और PD = 5 सेमी, तो PB की लंबाई क्या होगी? हल: PA × PB = PC × PD x(6 - x) = 5 × 8 x² - 6x – 40 = 0 x = 4, -10 PB = 4 PT² = PA × PB ∠1 = ∠2 AB = CD = प्रत्यक्ष सामान्य स्पर्श रेखा AB = CD = पार्श्व सामान्य स्पर्श रेखाएँ Q1. यदि दो वृत्तों की त्रिज्याएं 6 सेमी और 3 सेमी हैं और पार्श्व सामान्य स्पर्श रेखा की लंबाई 8 सेमी है, तो दोनों केंद्रों के बीच की दूरी क्या होगी? हल: पार्श्व सामान्य स्पर्श रेखा की लंबाई = हल किए गए उदाहरण Q1. दिए गए चित्र में, O वृत्त का केंद्र है और ∠AOB = 75°, तो ∠AEB क्या होगा? (a) 142.5 (b) 162.5 (c) 132.5 (d) 122.5 हल: ∠AOB = 75° ∠ADB = [वृत्त का केंद्र कोण प्रमुख आर्क के कोण का दो गुना होता है] AEBD एक चक्रीय चतुर्भुज है, तब ∠E ∠D = 180° ∠E = 180° - 37.5° ∠E = 142.5° Q2. एक वृत्त में, केंद्र कोण 120° है। प्रमुख कोण और लघु कोण का अनुपात ज्ञात करें। (a) 2:7 (b) 2:1 (c) 2:9 (d) 2:3 हल: [वृत्त का केंद्र कोण प्रमुख आर्क के कोण का दो गुना होता है] AEBD एक चक्रीय चतुर्भुज है, तब ∠AEB ∠ADB = 180° ∠AEB = 180° - 60° ∠AEB = 120° आवश्यक अनुपात = प्रमुख कोण : लघु कोण = 120° : 60° = 2 : 1 Q3. A, B और C वृत्त पर तीन बिंदु हैं, जिस पर एक स्पर्श रेखा A पर वृत्त को छूती है और चॉर्ड BC के विस्तारित भाग पर D से मिलती है। यदि कोण CAD = 39°, कोण CDA = 41° है, तो चॉर्ड BC द्वारा बनाया गया केंद्रीय कोण ज्ञात करें। (a) 122 (b) 123 (c) 132 (d) 142 हल: ∠ACB = ∠CAD + ∠CDA [दो आंतरिक कोणों का योग बाह्य कोण के विपरीत होता है] ∠ACB = 39° + 41° = 80° ∠BAE = ∠BCA = 80° [वैकल्पिक खंड] ∠EAB + ∠BAC + ∠CAD = 180° [रेखा कोण] 80° + ∠BAC + ∠CAD = 180° ∠BAC = 61° ∴ ∠BOC = 2 × ∠BAC [केंद्र कोण प्रमुख आर्क द्वारा बनाए गए कोण का दो गुना है] = 2 × 61° = 122° Q4. 16 सेमी और 9 सेमी त्रिज्या वाले दो बाहरी रूप से संपर्क करने वाले वृत्तों की सामान्य स्पर्श रेखा की लंबाई ज्ञात करें। (a) 12 सेमी (b) 24 सेमी (c) 13 सेमी (d) 28 सेमी हल: सामान्य स्पर्श रेखा की लंबाई = (दो वृत्तों के बीच की दूरी)² – (त्रिज्या1 – त्रिज्या2)² AB² = CD² - (16 – 9)² AB² = (16 + 9)² - (7)² AB² = 625 – 49 AB² = 576 AB = 24 सेमी Q5. ABC एक समद्विबाहु त्रिकोण है जिसमें एक वृत्त है जो вершि C के माध्यम से गुजरता है और AB उसी वृत्त पर D पर स्पर्श रेखा के रूप में कार्य करता है। AC और BC क्रमशः वृत्त पर E और F पर मिलते हैं। AC = BC = 4 सेमी और AB = 6 सेमी है। इसके अलावा, D AB का मध्य बिंदु है। EC : (AE - AD) का अनुपात क्या है? (a) 9:7 (b) 3:4 (c) 4:3 (d) 1:3 हल: यहाँ, AC और BC वृत्त के सेकेंट हैं और AB D पर स्पर्श रेखा है। अतः AE × AC = AD²
खंड → खंड का क्षेत्र = क्षेत्र OACB – त्रिभुज OAB का क्षेत्र → परिधि = आर्क ACB की लंबाई,Chord की लंबाई AB
वृत्त के महत्वपूर्ण गुण
हल किए गए उदाहरण

क्षेत्र खंड → क्षेत्र का खंड = क्षेत्र का क्षेत्र OACB – ΔOAB का क्षेत्र → परिमिति = आर्क ACB की लंबाई कॉर्ड लंबाई AB

प्रश्न 1: 120 डिग्री के केंद्रीय कोण और 8 सेमी के व्यास वाले वृत्त के खंड का क्षेत्रफल ज्ञात कीजिए। हल: क्षेत्र का खंड = 83.047

प्रश्न 2: 30 सेमी की आर्क लंबाई और 10 सेमी के व्यास वाले क्षेत्र का क्षेत्रफल ज्ञात कीजिए। हल: आर्क की लंबाई = क्षेत्र का क्षेत्र OAB =

प्रश्न 3: 21 सेमी के व्यास वाले वृत्त में आर्क केंद्र पर 72 डिग्री का कोण बनाता है। आर्क की लंबाई क्या है? हल: आर्क की लंबाई =

वृत्त के महत्वपूर्ण गुण

  • वृत्त के केंद्र से एक कॉर्ड पर खींची गई लंबवत कॉर्ड को आधा कर देती है। AM = MB
  • प्रश्न 1: AB = 8 सेमी और CD = 6 सेमी दो समानांतर कॉर्ड हैं जो वृत्त के केंद्र के एक ही तरफ हैं। उनके बीच की दूरी 1 सेमी है। व्यास की लंबाई ज्ञात कीजिए। हल: ON = x, AO = r। त्रिकोण AOE में r² = 16 (x-1)² और त्रिकोण OCN में r² = 9x² है।
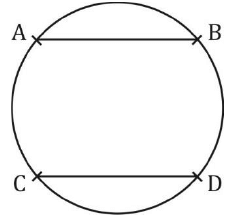
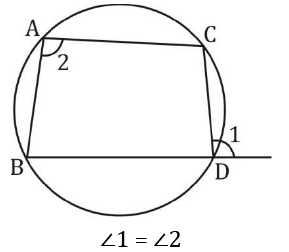
  • रक्त रेखाएं जो समान आर्क के लिए होती हैं, समान होती हैं। यदि AB = CD, तो ∠1 = ∠2
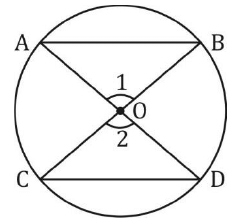
  • वृत्त के समान कॉर्ड केंद्र से समान दूरी पर होती हैं। यदि AB = CD, तो OX = OY
  • वृत्त के केंद्र पर आर्क द्वारा बनाया गया कोण उस परिपत्र के शेष भाग पर किसी भी बिंदु पर बनाया गया कोण का दो गुना होता है। x = 2y

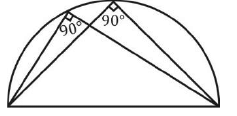
प्रश्न 4: एक वृत्त की कॉर्ड की लंबाई व्यास के बराबर है। उस कॉर्ड द्वारा बनाए गए प्रमुख खंड में बना कोण क्या है? हल: OA = OB = r। AB व्यास के बराबर है। इसलिए त्रिकोण OAB एक समभुज त्रिकोण है।

कोण OAB = 60°

प्रश्न 5: AC त्रिकोण ABC के परिक्रमण वृत्त का व्यास है। कॉर्ड ED व्यास AC के समानांतर है। यदि Angle CBE = 50°, तो Angle DEC का माप क्या होगा?

  • Angle CBE = 50°
  • Angle ABC = 90° (क्योंकि समकर्ण में हमेशा एक समकोण होता है)
  • Angle ABE = 90° - 50° = 40°
  • Angle ABE = Angle ACE = 40°
  • Angle ACE = Angle CED = 40° (वैकल्पिक कोण)

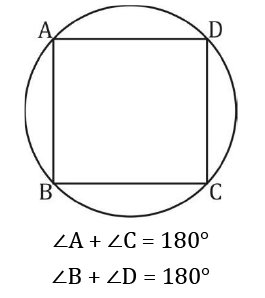
यदि, ABCD एक चक्रीय चतुर्भुज है

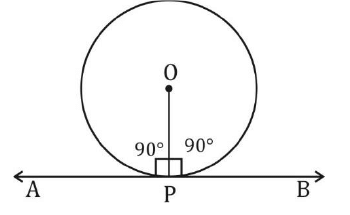
  • वृत्त के किसी भी बिंदु पर एक स्पर्श रेखा, उस बिंदु पर संपर्क के माध्यम से व्यास के प्रति लंबवत होती है। OP⊥AB
  • PA × PB = PC × PD

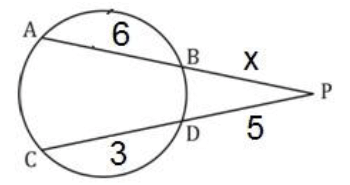
प्रश्न 6: यदि वृत्त AB और CD की कॉर्ड P पर बाह्य रूप से इंटरसेक्ट करती है। यदि AB = 6 सेमी, CD = 3 सेमी और PD = 5 सेमी है, तो PB की लंबाई ज्ञात करें। हल: PA × PB = PC × PD, x(6 x)= 5 × 8, x² 6x – 40 = 0, x = 4, -10 PB = 4

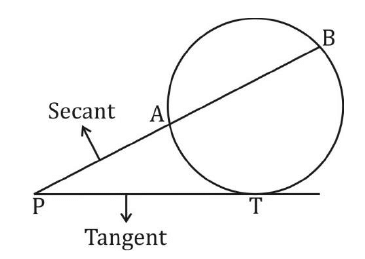
PT² = PA × PB, ∠1 = ∠2

प्रश्न 7: यदि दो वृत्तों की त्रिज्याएँ 6 सेमी और 3 सेमी हैं और ट्रांसवर्स सामान्य स्पर्श रेखा की लंबाई 8 सेमी है, तो दोनों केंद्रों के बीच की दूरी क्या होगी? हल: ट्रांसवर्स सामान्य स्पर्श रेखा की लंबाई =

उदाहरण:

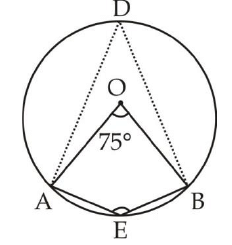
  • प्रश्न 8: दिए गए चित्र में, O वृत्त का केंद्र है और ∠AOB = 75°, तो ∠AEB क्या होगा? (क) 142.5 (ख) 162.5 (ग) 132.5 (घ) 122.5 हल: ∠AOB = 75°, ∠ADB = [वृत्त का केंद्र कोण प्रमुख आर्क के कोण का दो गुना है]

AEBD एक चक्रीय चतुर्भुज है, तो ∠E + ∠D = 180°, ∠E = 37.5° = 180° - ∠E = 142.5°

प्रश्न 9: एक वृत्त में, केंद्र का कोण 120° है। प्रमुख कोण और छोटे कोण का अनुपात ज्ञात करें। (क) 2:7 (ख) 2:1 (ग) 2:9 (घ) 2:3 हल: [वृत्त के केंद्र का कोण प्रमुख आर्क के कोण का दो गुना है]

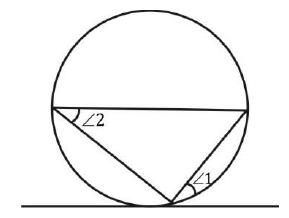
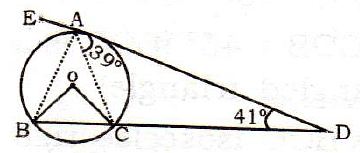
प्रश्न 10: A, B और C वृत्त पर तीन बिंदु हैं, जैसे कि एक स्पर्श रेखा A पर स्पर्श करती है और BC की विस्तारित कॉर्ड पर D पर इंटरसेक्ट करती है। यदि कोण CAD = 39°, कोण CDA = 41° है, तो कॉर्ड BC द्वारा बनाए गए केंद्रीय कोण का माप ज्ञात कीजिए। (क) 122 (ख) 123 (ग) 132 (घ) 142 हल:

  • ∠ACB = ∠CAD + ∠CDA [दो आंतरिक कोण का योग बाह्य कोण के बराबर होता है]
  • ∠ACB = 39° + 41° = 80°
  • ∠BAE = ∠BCA = 80° [वैकल्पिक खंड]
  • ∠EAB + ∠BAC + ∠CAD = 180° [रेखीय कोण]
  • 80° + ∠BAC + ∠CAD = 180°, ∠BAC = 61°
  • ∴ ∠BOC = 2 × ∠BAC [केंद्रीय कोण हमेशा प्रमुख आर्क द्वारा बनाए गए कोण का दो गुना होता है] = 2 × 61° = 122°

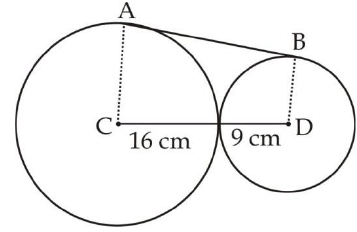
प्रश्न 11: 16 सेमी और 9 सेमी त्रिज्या वाले दो बाह्य संपर्क वृत्तों की सामान्य स्पर्श रेखा की लंबाई ज्ञात कीजिए? (क) 12 सेमी (ख) 24 सेमी (ग) 13 सेमी (घ) 28 सेमी हल: सामान्य स्पर्श रेखा की लंबाई = (दो वृत्तों के बीच की दूरी)² – (त्रिज्या1 – त्रिज्या2)²

  • AB² = CD² - (16 – 9)²
  • AB² = (16 + 9)² - (7)²
  • AB² = 625 – 49
  • AB² = 576, AB = 24 सेमी

प्रश्न 12: ABC एक समद्विबाहु त्रिकोण है, एक वृत्त ऐसा है कि यह शिखर C के माध्यम से गुजरता है और AB उसी वृत्त पर D पर स्पर्श रेखा के रूप में कार्य करता है। AC और BC वृत्त पर E और F पर इंटरसेक्ट करते हैं। AC = BC = 4 सेमी और AB = 6 सेमी है। D AB का मध्य बिंदु है। EC : (AE AD) का अनुपात क्या है? (क) 9:7 (ख) 3:4 (ग) 4:3 (घ) 1:3 हल: यहां, AC और BC वृत्त के सेकेंट हैं और AB D पर स्पर्श रेखा है। इसलिए AE × AC = AD²

सेक्टर सेगमेंट → क्षेत्रफल का सेगमेंट = क्षेत्रफल का सेक्टर OACB – क्षेत्रफल का ∆OAB → परिमाप = आर्क ACB की लंबाई चॉर्ड की लंबाई AB Q1. एक वृत्त के सेगमेंट का क्षेत्रफल ज्ञात करें जिसमें केंद्रीय कोण 120 डिग्री और त्रिज्या 8 सेमी है। हल: क्षेत्रफल का सेगमेंट = 83.047 Q2. एक सेक्टर का क्षेत्रफल ज्ञात करें जिसमें आर्क की लंबाई 30 सेमी और त्रिज्या 10 सेमी है। हल: आर्क की लंबाई = सेक्टर का क्षेत्रफल OAB = Q3. एक वृत्त की त्रिज्या 21 सेमी है और आर्क केंद्र पर 72 डिग्री का कोण बनाता है। आर्क की लंबाई क्या है? हल: आर्क की लंबाई = वृत्त के महत्वपूर्ण गुण - वृत्त के केंद्र से एक चॉर्ड पर खींची गई लंबवत रेखा चॉर्ड को आधा करती है। AM = MB Q1. AB = 8 सेमी और CD = 6 सेमी दो समानांतर चॉर्ड हैं जो वृत्त के केंद्र के एक ही तरफ हैं। उनके बीच की दूरी 1 सेमी है। त्रिज्या की लंबाई ज्ञात करें। हल: ON = x, AO = r त्रिकोण AOE में r² = 16 (x-1)² त्रिकोण OCN में r² = 9 x² 16 (x-1)² = 9 x² x = 4, r² = 9, r = 5 सेमी - समान आर्क के लिए चॉर्ड समान होते हैं। यदि AB = CD, तो ∠1 = ∠2 - वृत्त के समान चॉर्ड केंद्र से समान दूरी पर होते हैं। यदि AB = CD, तो OX = OY - वृत्त के केंद्र पर आर्क द्वारा बनाया गया कोण उस आर्क द्वारा वृत्त के शेष भाग के किसी भी बिंदु पर बनाये गए कोण का दो गुना होता है। x = 2y Q1. एक वृत्त की चॉर्ड की लंबाई उसके त्रिज्या के बराबर है। इस चॉर्ड द्वारा बड़ा सेगमेंट में जो कोण बनता है वो क्या है? हल: OA = OB = r AB त्रिज्या के समान है अतः त्रिकोण OAB एक समद्विबाहु त्रिकोण है कोण OAB = 60° कोण ACB, जो चॉर्ड बनाता है बड़ा कोण = - वृत्त के समान सेगमेंट में कोण समान होते हैं। - अर्धवृत्त में हमेशा दाएं कोण होता है। Q1. AC त्रिकोण ABC का व्यास है। चॉर्ड ED व्यास AC के समानांतर है। यदि कोण CBE = 50°, तो कोण DEC का माप क्या होगा? कोण CBE = 50° कोण ABC = 90° (अर्धवृत्त में कोण हमेशा दाएं होता है) कोण ABE = 90° - 50° = 40° कोण ABE = कोण ACE = 40° कोण ACE = कोण CED = 40° (वैकल्पिक कोण) यदि ABCD एक चक्रीय चतुर्भुज है: - वृत्त के किसी बिंदु पर एक स्पर्श रेखा उस बिंदु पर त्रिज्या के प्रति लंबवत होती है। OP⊥AB - PA × PB = PC × PD - PA × PB = PC × PD Q1. वृत्त के चॉर्ड AB और CD की बाहरी रूप से P पर प्रतिच्छेदन होता है। यदि AB = 6 सेमी, CD = 3 सेमी और PD = 5 सेमी, तो PB की लंबाई क्या होगी? हल: PA × PB = PC × PD x(6 - x) = 5 × 8 x² - 6x – 40 = 0 x = 4, -10 PB = 4 PT² = PA × PB ∠1 = ∠2 AB = CD = प्रत्यक्ष सामान्य स्पर्श रेखा AB = CD = पार्श्व सामान्य स्पर्श रेखाएँ Q1. यदि दो वृत्तों की त्रिज्याएं 6 सेमी और 3 सेमी हैं और पार्श्व सामान्य स्पर्श रेखा की लंबाई 8 सेमी है, तो दोनों केंद्रों के बीच की दूरी क्या होगी? हल: पार्श्व सामान्य स्पर्श रेखा की लंबाई = हल किए गए उदाहरण Q1. दिए गए चित्र में, O वृत्त का केंद्र है और ∠AOB = 75°, तो ∠AEB क्या होगा? (a) 142.5 (b) 162.5 (c) 132.5 (d) 122.5 हल: ∠AOB = 75° ∠ADB = [वृत्त का केंद्र कोण प्रमुख आर्क के कोण का दो गुना होता है] AEBD एक चक्रीय चतुर्भुज है, तब ∠E ∠D = 180° ∠E = 180° - 37.5° ∠E = 142.5° Q2. एक वृत्त में, केंद्र कोण 120° है। प्रमुख कोण और लघु कोण का अनुपात ज्ञात करें। (a) 2:7 (b) 2:1 (c) 2:9 (d) 2:3 हल: [वृत्त का केंद्र कोण प्रमुख आर्क के कोण का दो गुना होता है] AEBD एक चक्रीय चतुर्भुज है, तब ∠AEB ∠ADB = 180° ∠AEB = 180° - 60° ∠AEB = 120° आवश्यक अनुपात = प्रमुख कोण : लघु कोण = 120° : 60° = 2 : 1 Q3. A, B और C वृत्त पर तीन बिंदु हैं, जिस पर एक स्पर्श रेखा A पर वृत्त को छूती है और चॉर्ड BC के विस्तारित भाग पर D से मिलती है। यदि कोण CAD = 39°, कोण CDA = 41° है, तो चॉर्ड BC द्वारा बनाया गया केंद्रीय कोण ज्ञात करें। (a) 122 (b) 123 (c) 132 (d) 142 हल: ∠ACB = ∠CAD + ∠CDA [दो आंतरिक कोणों का योग बाह्य कोण के विपरीत होता है] ∠ACB = 39° + 41° = 80° ∠BAE = ∠BCA = 80° [वैकल्पिक खंड] ∠EAB + ∠BAC + ∠CAD = 180° [रेखा कोण] 80° + ∠BAC + ∠CAD = 180° ∠BAC = 61° ∴ ∠BOC = 2 × ∠BAC [केंद्र कोण प्रमुख आर्क द्वारा बनाए गए कोण का दो गुना है] = 2 × 61° = 122° Q4. 16 सेमी और 9 सेमी त्रिज्या वाले दो बाहरी रूप से संपर्क करने वाले वृत्तों की सामान्य स्पर्श रेखा की लंबाई ज्ञात करें। (a) 12 सेमी (b) 24 सेमी (c) 13 सेमी (d) 28 सेमी हल: सामान्य स्पर्श रेखा की लंबाई = (दो वृत्तों के बीच की दूरी)² – (त्रिज्या1 – त्रिज्या2)² AB² = CD² - (16 – 9)² AB² = (16 + 9)² - (7)² AB² = 625 – 49 AB² = 576 AB = 24 सेमी Q5. ABC एक समद्विबाहु त्रिकोण है जिसमें एक वृत्त है जो вершि C के माध्यम से गुजरता है और AB उसी वृत्त पर D पर स्पर्श रेखा के रूप में कार्य करता है। AC और BC क्रमशः वृत्त पर E और F पर मिलते हैं। AC = BC = 4 सेमी और AB = 6 सेमी है। इसके अलावा, D AB का मध्य बिंदु है। EC : (AE - AD) का अनुपात क्या है? (a) 9:7 (b) 3:4 (c) 4:3 (d) 1:3 हल: यहाँ, AC और BC वृत्त के सेकेंट हैं और AB D पर स्पर्श रेखा है। अतः AE × AC = AD²

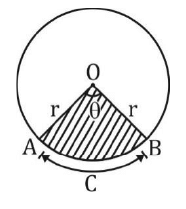
संक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

खंड → खंड का क्षेत्र = क्षेत्र OACB – त्रिभुज OAB का क्षेत्र → परिधि = आर्क ACB की लंबाई,Chord की लंबाई AB

Q1. एक वृत्त के खंड का क्षेत्रफल ज्ञात करें जिसका केंद्रीय कोण 120 डिग्री और त्रिज्या 8 सेमी है।

समाधान: खंड का क्षेत्रफल = 83.047

Q2. एक सेक्टर का क्षेत्रफल ज्ञात करें जिसकी आर्क लंबाई 30 सेमी और त्रिज्या 10 सेमी है।

समाधान: आर्क की लंबाई = सेक्टर का क्षेत्र OAB =

Q3. एक वृत्त की त्रिज्या 21 सेमी है और आर्क केंद्र पर 72 डिग्री का कोण बनाता है। आर्क की लंबाई क्या है?

समाधान: आर्क की लंबाई =

वृत्त की महत्वपूर्ण विशेषताएँ:

  • वृत्त के केंद्र से किसी कोर्ड पर खींची गई लंबवत रेखा कोर्ड को आधा कर देती है। AM = MB
  • Q1. AB = 8 सेमी और CD = 6 सेमी दो समानांतर कोर्ड हैं जो वृत्त के केंद्र के एक ही तरफ हैं। उनके बीच की दूरी 1 सेमी है। त्रिज्या की लंबाई ज्ञात करें।
  • समाधान: ON = x, AO = r, त्रिभुज AOE में r² = 16 (x-1)², त्रिभुज OCN में r² = 9x²।
  • 16 (x-1)² = 9x²
  • x = 4, r² = 9, r = 5 सेमी

समान आर्क के लिए संबंधित कोर्ड समान होते हैं। यदि AB = CD, तो ∠1 = ∠2

समान कोर्ड वृत्त के केंद्र से समान दूरी पर होते हैं। यदि AB = CD, तो OX = OY

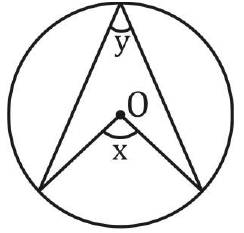
किसी आर्क द्वारा वृत्त के केंद्र पर बनता कोण उस आर्क द्वारा वृत्त के बाकी हिस्से पर किसी भी बिंदु पर बनते कोण का दो गुना होता है। x = 2y

Q1. एक वृत्त की कोर्ड की लंबाई वृत्त की त्रिज्या के बराबर है। इस कोर्ड द्वारा वृत्त के प्रमुख खंड में बनता कोण क्या है?

समाधान: OA = OB = r, AB त्रिज्या के बराबर है। इसलिए त्रिभुज OAB एक समबाहु त्रिभुज है।

∠OAB = 60°

वृत्त के समान खंड में कोण समान होते हैं। एक अर्द्धवृत्त में हमेशा एक समकोण होता है।

Q1. AC त्रिभुज ABC का व्यास है। कोर्ड ED व्यास AC के समानांतर है। यदि ∠CBE = 50°, तो कोण DEC का माप क्या है?

∠CBE = 50°, ∠ABC = 90° (अर्द्धवृत्त में हमेशा समकोण होता है)

∠ABE = 90° - 50° = 40°, ∠ABE = ∠ACE = 40°, ∠ACE = ∠CED = 40° (वैकल्पिक कोण)

यदि ABCD एक चक्रीय चतुर्भुज है।

किसी वृत्त के किसी बिंदु पर टेन्गेंट उस बिंदु पर संपर्क के माध्यम से त्रिज्या के प्रति लंबवत होती है। OP⊥AB

PA × PB = PC × PD

Q1. वृत्त के कोर्ड AB और CD बाहरी रूप से P पर इंटरसेक्ट होते हैं। यदि AB = 6 सेमी, CD = 3 सेमी और PD = 5 सेमी है, तो PB की लंबाई क्या होगी?

समाधान: PA × PB = PC × PD

x(6 - x) = 5 × 8

x² - 6x - 40 = 0

x = 4, -10

PB = 4

PT² = PA × PB

∠1 = ∠2, AB = CD

प्रत्यक्ष सामान्य टेन्गेंट, AB = CD

परावर्ती सामान्य टेन्गेंट

Q1. यदि दो वृत्तों की त्रिज्याएँ 6 सेमी और 3 सेमी हों और परावर्ती सामान्य टेन्गेंट की लंबाई 8 सेमी हो, तो दोनों केंद्रों के बीच की दूरी क्या होगी?

समाधान: परावर्ती सामान्य टेन्गेंट की लंबाई =

हल किए गए उदाहरण:

Q1. दिए गए चित्र में, O वृत्त का केंद्र है और ∠AOB = 75°, तो ∠AEB क्या होगा?

  • (a) 142.5
  • (b) 162.5
  • (c) 132.5
  • (d) 122.5

समाधान: ∠AOB = 75° ∠ADB = [वृत्त का केंद्र कोण प्रमुख आर्क के कोण का दो गुना होता है]

AEBD एक चक्रीय चतुर्भुज है, इसलिए ∠E + ∠D = 180°

∠E = 180° - 37.5° = 142.5°

Q2. एक वृत्त में, केंद्र का कोण 120° है। प्रमुख कोण और छोटे कोण का अनुपात ज्ञात करें।

  • (a) 2:7
  • (b) 2:1
  • (c) 2:9
  • (d) 2:3

समाधान: [वृत्त का केंद्र कोण प्रमुख आर्क के कोण का दो गुना होता है]

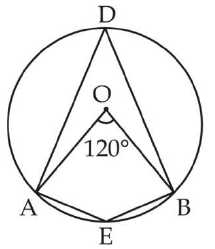
AEBD एक चक्रीय चतुर्भुज है, इसलिए ∠AEB + ∠ADB = 180°

∠AEB = 180° - 60° = 120°

आवश्यक अनुपात = प्रमुख कोण : छोटे कोण = 120° : 60° = 2 : 1

Q3. A, B और C वृत्त पर तीन बिंदु हैं, जहाँ एक टेन्गेंट वृत्त पर A पर स्पर्श करती है और कोर्ड BC के विस्तारित भाग पर D पर इंटरसेक्ट करती है। यदि ∠CAD = 39° और ∠CDA = 41° है, तो कोर्ड BC द्वारा बनाए गए केंद्रीय कोण का मान ज्ञात करें।

  • (a) 122
  • (b) 123
  • (c) 132
  • (d) 142

समाधान: ∠ACB = ∠CAD + ∠CDA [दो आंतरिक कोणों का योग बाह्य कोण के बराबर होता है]

∠ACB = 39° + 41° = 80°

∠BAE = ∠BCA = 80° [वैकल्पिक खंड]

∠EAB + ∠BAC + ∠CAD = 180° [सीधी कोण]

80° + ∠BAC + ∠CAD = 180°

∠BAC = 61°

∴ ∠BOC = 2 × ∠BAC [केंद्रीय कोण प्रमुख आर्क द्वारा बनाए गए कोण का दो गुना होता है]

= 2 × 61° = 122°

Q4. 16 सेमी और 9 सेमी त्रिज्या वाले दो वृत्तों के बीच सामान्य टेन्गेंट की लंबाई ज्ञात करें।

  • (a) 12 सेमी
  • (b) 24 सेमी
  • (c) 13 सेमी
  • (d) 28 सेमी

समाधान: सामान्य टेन्गेंट की लंबाई = (दो वृत्तों के बीच की दूरी)² – (त्रिज्या1 – त्रिज्या2)²

AB² = CD² - (16 – 9)²

AB² = (16 + 9)² - (7)²

AB² = 625 – 49

AB² = 576

AB = 24 सेमी

Q5. ABC एक समद्विबाहु त्रिभुज है। एक वृत्त ऐसा है कि यह शीर्ष C से गुजरता है और AB वृत्त के लिए D पर टेन्गेंट के रूप में कार्य करता है। AC और BC क्रमशः वृत्त को E और F पर इंटरसेक्ट करते हैं। AC = BC = 4 सेमी और AB = 6 सेमी है। D AB का मध्य बिंदु है। EC : (AE + AD) का अनुपात क्या है?

  • (a) 9:7
  • (b) 3:4
  • (c) 4:3
  • (d) 1:3

समाधान: यहाँ, AC और BC वृत्त के सेकेंट हैं और AB D पर टेन्गेंट है।

∴ AE × AC = AD²

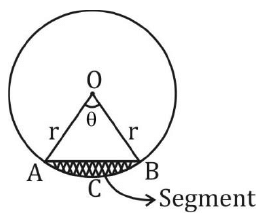
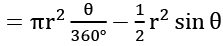
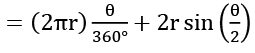
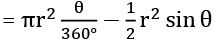
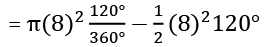
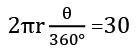
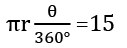
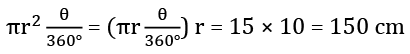
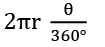
संक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

वृत्त के महत्वपूर्ण गुण

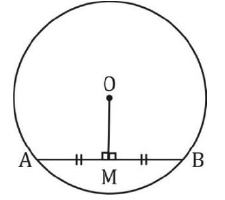
वृत्त के केंद्र से एक रेखा जो एक तंतु पर लंबवत होती है, उस तंतु को आधा करती है। AM = MB

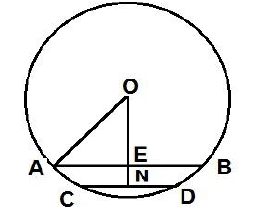
  • प्रश्न 1: AB = 8 सेमी और CD = 6 सेमी दो समानांतर तंतु हैं जो वृत्त के केंद्र के एक ही ओर हैं। उनके बीच की दूरी 1 सेमी है। त्रिज्या की लंबाई ज्ञात कीजिए।

हल: मान लेते हैं ON = x, AO = r

  • त्रिकोण AOE में: r2 = 16 (x-1)2
  • त्रिकोण OCN में: r2 = 9 x2

16 (x-1)2 = 9 x2

x = 4, r2 = 9 + 16, r = 5 सेमी

समान आर्क के लिए तंतु समान होते हैं। यदि AB = CD तब समान तंतु केंद्र पर समान कोण बनाते हैं। यदि AB = CD तब ∠1 = ∠2

वृत्त के समान तंतु केंद्र से समान दूरी पर होते हैं। यदि AB = CD तब OX = OY

वृत्त के एक आर्क द्वारा केंद्र पर बनता कोण, उस आर्क द्वारा वृत्त के शेष भाग पर किसी भी बिंदु पर बनते कोण का दोगुना होता है। x = 2y

  • प्रश्न 2: यदि एक तंतु की लंबाई वृत्त की त्रिज्या के बराबर है। तब यह तंतु वृत्त के बड़े खंड में किस कोण को बनाता है?

हल: OA = OB = r, AB त्रिज्या के बराबर है। इसलिए त्रिकोण OAB एक समबाहु त्रिकोण है।

  • कोण OAB = 60°
  • ACB, बड़ा कोण बनाता है = वृत्त के समान खंड में समान कोण होते हैं।
  • वृत्त के अर्धवृत्त में हमेशा एक समकोण होता है।

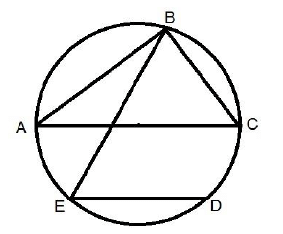
प्रश्न 3: AC त्रिभुज ABC की परिघात वृत्त का व्यास है। तंतु ED व्यास AC के समानांतर है। यदि कोण CBE = 50°, तो कोण DEC का माप क्या होगा?

  • कोण CBE = 50°
  • कोण ABC = 90° (अर्धवृत्त में हमेशा समकोण होता है)
  • कोण ABE = 90° - 50° = 40°
  • कोण ABE = कोण ACE = 40°
  • कोण ACE = कोण CED = 40° (वैकल्पिक कोण)

यदि ABCD एक चक्रीय चतुर्भुज है। एक वृत्त के किसी भी बिंदु पर तंतु उस बिंदु पर संपर्क के माध्यम से त्रिज्या पर लंबवत होता है। OP⊥AB

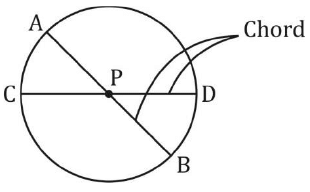
PA × PB = PC × PD

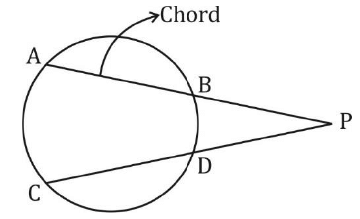
  • प्रश्न 4: वृत्त के तंतु AB और CD बाहर से P पर मिलते हैं। यदि AB = 6 सेमी, CD = 3 सेमी और PD = 5 सेमी है, तो PB की लंबाई ज्ञात कीजिए।

हल: PA × PB = PC × PD

x(6x) = 5 × 8

x2 - 6x - 40 = 0

x = 4 , -10

PB = 4

PT2 = PA × PB

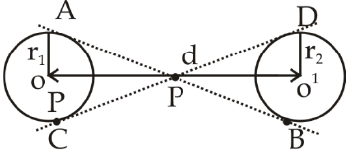
प्रश्न 5: यदि दो वृत्तों की त्रिज्याएँ क्रमशः 6 सेमी और 3 सेमी हैं और पार्श्व तंतु की लंबाई 8 सेमी है, तो दो केंद्रों के बीच की दूरी क्या होगी?

हल: पार्श्व तंतु की लंबाई = (दो वृत्तों के बीच की दूरी)2 - (त्रिज्या1 - त्रिज्या2)2

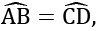
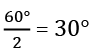
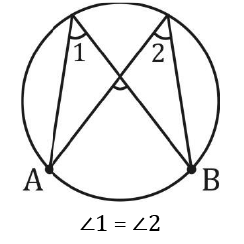
संक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

∠1 = ∠2 AB = CD = प्रत्यक्ष सामान्य टेन्जेंट AB = CD आवर्तक सामान्य टेन्जेंट

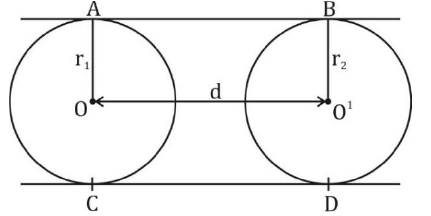
प्रश्न 1: यदि दो वृत्तों की त्रिज्याएँ 6 सेमी और 3 सेमी हों और आवर्तक सामान्य टेन्जेंट की लंबाई 8 सेमी हो, तो दोनों केंद्रों के बीच की दूरी क्या होगी?

हल: आवर्तक सामान्य टेन्जेंट की लंबाई =

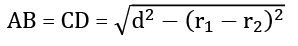
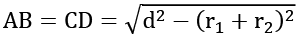
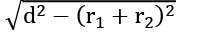
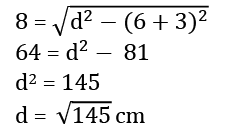
संक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA संक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA संक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA संक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA संक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA संक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

हल किए गए उदाहरण

Q1. दिए गए चित्र में, O वृत्त का केन्द्र है और ∠AOB = 75° है, तब ∠AEB क्या होगा? (a) 142.5 (b) 162.5 (c) 132.5 (d) 122.5

हल. ∠AOB = 75°

∠ADB = [वृत्त का केन्द्र कोण प्रमुख आर्क के कोण का दो गुना होता है]

AEBD एक चक्रीय चतुर्भुज है, इसलिए, ∠E + ∠D = 180°

∠E + 37.5° = 180°

∴ ∠E = 142.5°

Q2. एक वृत्त में, केन्द्र कोण 120° है। प्रमुख और गौण कोण का अनुपात ज्ञात करें? (a) 2:7 (b) 2:1 (c) 2:9 (d) 2:3

हल. [वृत्त का केन्द्र कोण प्रमुख आर्क के कोण का दो गुना होता है]

AEBD एक चक्रीय चतुर्भुज है, इसलिए, ∠AEB + ∠ADB = 180°

∠AEB = 180° - 60°

∴ ∠AEB = 120°

आवश्यक अनुपात = प्रमुख कोण : गौण कोण = 120° : 60° = 2 : 1

Q3. A, B & C वृत्त पर तीन बिंदु हैं, जिसमें एक स्पर्शरेखा A पर वृत्त को छूती है और BC के विस्तारित भाग पर D को काटती है। यदि कोण CAD = 39°, कोण CDA = 41° है, तो BC द्वारा बनाए गए केन्द्र कोण को ज्ञात करें? (a) 122 (b) 123 (c) 132 (d) 142

हल. ∠ACB = ∠CAD + ∠CDA [दो आंतरिक कोणों का योग बाहरी कोण के विपरीत होता है]

∠ACB = 39° + 41° = 80°

∠BAE = ∠BCA = 80° [वैकल्पिक खंड]

∠EAB + ∠BAC + ∠CAD = 180° [रेखीय कोण]

80° + ∠BAC + ∠CAD = 180°

∴ ∠BAC = 61°

∴ ∠BOC = 2 × ∠BAC [केन्द्र कोण प्रमुख आर्क द्वारा एकत्रित कोण का दो गुना होता है] = 2 × 61° = 122°

Q4. 16 सेमी और 9 सेमी त्रिज्या के दो वृत्तों की सामान्य स्पर्शरेखा की लंबाई ज्ञात करें? (a) 12 सेमी (b) 24 सेमी (c) 13 सेमी (d) 28 सेमी

हल. सामान्य स्पर्शरेखा की लंबाई = (दो वृत्तों के बीच की दूरी)² – (Radius1 – Radius2)²

AB² = CD² - (16 – 9)²

AB² = (16 + 9)² - (7)²

AB² = 625 – 49

AB² = 576

∴ AB = 24 सेमी

Q5. ABC एक समबाहु त्रिकोण है, एक वृत्त ऐसा है कि यह C शीर्ष बिंदु से गुजरता है और AB उसी वृत्त पर D पर स्पर्शरेखा के रूप में कार्य करता है। AC और BC क्रमशः वृत्त को E और F पर काटते हैं, AC = BC = 4 सेमी और AB = 6 सेमी है। इसके अलावा, D, AB का मध्य बिंदु है। EC : (AE + AD) का अनुपात क्या है? (a) 9:7 (b) 3:4 (c) 4:3 (d) 1:3

हल. यहाँ, AC और BC वृत्त के सेकेंट हैं और AB D पर स्पर्शरेखा है, इसलिए AE × AC = AD²

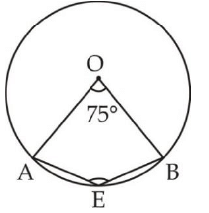
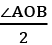
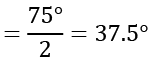
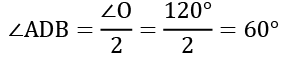
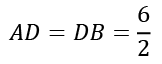
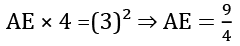
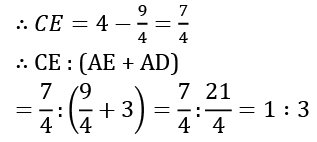
I'm sorry, but it appears that your request is missing the specific chapter notes that need to be translated into Hindi. Could you please provide the text you would like to have translated?संक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TAसंक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA
The document संक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA is a part of the RRB NTPC/ASM/CA/TA Course Mathematics for RRB NTPC (Hindi).
All you need of RRB NTPC/ASM/CA/TA at this link: RRB NTPC/ASM/CA/TA
142 videos|172 docs|185 tests
Join Course for Free
About this Document
Oct 18, 2025 Last updated
Related Exams
Document Description: संक्षेप: वृत्त for RRB NTPC/ASM/CA/TA 2025 is part of Mathematics for RRB NTPC (Hindi) preparation. The notes and questions for संक्षेप: वृत्त have been prepared according to the RRB NTPC/ASM/CA/TA exam syllabus. Information about संक्षेप: वृत्त covers topics like सेक्टर सेगमेंट → क्षेत्रफल का सेगमेंट = क्षेत्रफल का सेक्टर OACB – क्षेत्रफल का ∆OAB → परिमाप = आर्क ACB की लंबाई चॉर्ड की लंबाई AB Q1. एक वृत्त के सेगमेंट का क्षेत्रफल ज्ञात करें जिसमें केंद्रीय कोण 120 डिग्री और त्रिज्या 8 सेमी है। हल: क्षेत्रफल का सेगमेंट = 83.047 Q2. एक सेक्टर का क्षेत्रफल ज्ञात करें जिसमें आर्क की लंबाई 30 सेमी और त्रिज्या 10 सेमी है। हल: आर्क की लंबाई = सेक्टर का क्षेत्रफल OAB = Q3. एक वृत्त की त्रिज्या 21 सेमी है और आर्क केंद्र पर 72 डिग्री का कोण बनाता है। आर्क की लंबाई क्या है? हल: आर्क की लंबाई = वृत्त के महत्वपूर्ण गुण - वृत्त के केंद्र से एक चॉर्ड पर खींची गई लंबवत रेखा चॉर्ड को आधा करती है। AM = MB Q1. AB = 8 सेमी और CD = 6 सेमी दो समानांतर चॉर्ड हैं जो वृत्त के केंद्र के एक ही तरफ हैं। उनके बीच की दूरी 1 सेमी है। त्रिज्या की लंबाई ज्ञात करें। हल: ON = x, AO = r त्रिकोण AOE में r² = 16 (x-1)² त्रिकोण OCN में r² = 9 x² 16 (x-1)² = 9 x² x = 4, r² = 9, r = 5 सेमी - समान आर्क के लिए चॉर्ड समान होते हैं। यदि AB = CD, तो ∠1 = ∠2 - वृत्त के समान चॉर्ड केंद्र से समान दूरी पर होते हैं। यदि AB = CD, तो OX = OY - वृत्त के केंद्र पर आर्क द्वारा बनाया गया कोण उस आर्क द्वारा वृत्त के शेष भाग के किसी भी बिंदु पर बनाये गए कोण का दो गुना होता है। x = 2y Q1. एक वृत्त की चॉर्ड की लंबाई उसके त्रिज्या के बराबर है। इस चॉर्ड द्वारा बड़ा सेगमेंट में जो कोण बनता है वो क्या है? हल: OA = OB = r AB त्रिज्या के समान है अतः त्रिकोण OAB एक समद्विबाहु त्रिकोण है कोण OAB = 60° कोण ACB, जो चॉर्ड बनाता है बड़ा कोण = - वृत्त के समान सेगमेंट में कोण समान होते हैं। - अर्धवृत्त में हमेशा दाएं कोण होता है। Q1. AC त्रिकोण ABC का व्यास है। चॉर्ड ED व्यास AC के समानांतर है। यदि कोण CBE = 50°, तो कोण DEC का माप क्या होगा? कोण CBE = 50° कोण ABC = 90° (अर्धवृत्त में कोण हमेशा दाएं होता है) कोण ABE = 90° - 50° = 40° कोण ABE = कोण ACE = 40° कोण ACE = कोण CED = 40° (वैकल्पिक कोण) यदि ABCD एक चक्रीय चतुर्भुज है: - वृत्त के किसी बिंदु पर एक स्पर्श रेखा उस बिंदु पर त्रिज्या के प्रति लंबवत होती है। OP⊥AB - PA × PB = PC × PD - PA × PB = PC × PD Q1. वृत्त के चॉर्ड AB और CD की बाहरी रूप से P पर प्रतिच्छेदन होता है। यदि AB = 6 सेमी, CD = 3 सेमी और PD = 5 सेमी, तो PB की लंबाई क्या होगी? हल: PA × PB = PC × PD x(6 - x) = 5 × 8 x² - 6x – 40 = 0 x = 4, -10 PB = 4 PT² = PA × PB ∠1 = ∠2 AB = CD = प्रत्यक्ष सामान्य स्पर्श रेखा AB = CD = पार्श्व सामान्य स्पर्श रेखाएँ Q1. यदि दो वृत्तों की त्रिज्याएं 6 सेमी और 3 सेमी हैं और पार्श्व सामान्य स्पर्श रेखा की लंबाई 8 सेमी है, तो दोनों केंद्रों के बीच की दूरी क्या होगी? हल: पार्श्व सामान्य स्पर्श रेखा की लंबाई = हल किए गए उदाहरण Q1. दिए गए चित्र में, O वृत्त का केंद्र है और ∠AOB = 75°, तो ∠AEB क्या होगा? (a) 142.5 (b) 162.5 (c) 132.5 (d) 122.5 हल: ∠AOB = 75° ∠ADB = [वृत्त का केंद्र कोण प्रमुख आर्क के कोण का दो गुना होता है] AEBD एक चक्रीय चतुर्भुज है, तब ∠E ∠D = 180° ∠E = 180° - 37.5° ∠E = 142.5° Q2. एक वृत्त में, केंद्र कोण 120° है। प्रमुख कोण और लघु कोण का अनुपात ज्ञात करें। (a) 2:7 (b) 2:1 (c) 2:9 (d) 2:3 हल: [वृत्त का केंद्र कोण प्रमुख आर्क के कोण का दो गुना होता है] AEBD एक चक्रीय चतुर्भुज है, तब ∠AEB ∠ADB = 180° ∠AEB = 180° - 60° ∠AEB = 120° आवश्यक अनुपात = प्रमुख कोण : लघु कोण = 120° : 60° = 2 : 1 Q3. A, B और C वृत्त पर तीन बिंदु हैं, जिस पर एक स्पर्श रेखा A पर वृत्त को छूती है और चॉर्ड BC के विस्तारित भाग पर D से मिलती है। यदि कोण CAD = 39°, कोण CDA = 41° है, तो चॉर्ड BC द्वारा बनाया गया केंद्रीय कोण ज्ञात करें। (a) 122 (b) 123 (c) 132 (d) 142 हल: ∠ACB = ∠CAD + ∠CDA [दो आंतरिक कोणों का योग बाह्य कोण के विपरीत होता है] ∠ACB = 39° + 41° = 80° ∠BAE = ∠BCA = 80° [वैकल्पिक खंड] ∠EAB + ∠BAC + ∠CAD = 180° [रेखा कोण] 80° + ∠BAC + ∠CAD = 180° ∠BAC = 61° ∴ ∠BOC = 2 × ∠BAC [केंद्र कोण प्रमुख आर्क द्वारा बनाए गए कोण का दो गुना है] = 2 × 61° = 122° Q4. 16 सेमी और 9 सेमी त्रिज्या वाले दो बाहरी रूप से संपर्क करने वाले वृत्तों की सामान्य स्पर्श रेखा की लंबाई ज्ञात करें। (a) 12 सेमी (b) 24 सेमी (c) 13 सेमी (d) 28 सेमी हल: सामान्य स्पर्श रेखा की लंबाई = (दो वृत्तों के बीच की दूरी)² – (त्रिज्या1 – त्रिज्या2)² AB² = CD² - (16 – 9)² AB² = (16 + 9)² - (7)² AB² = 625 – 49 AB² = 576 AB = 24 सेमी Q5. ABC एक समद्विबाहु त्रिकोण है जिसमें एक वृत्त है जो вершि C के माध्यम से गुजरता है और AB उसी वृत्त पर D पर स्पर्श रेखा के रूप में कार्य करता है। AC और BC क्रमशः वृत्त पर E और F पर मिलते हैं। AC = BC = 4 सेमी और AB = 6 सेमी है। इसके अलावा, D AB का मध्य बिंदु है। EC : (AE - AD) का अनुपात क्या है? (a) 9:7 (b) 3:4 (c) 4:3 (d) 1:3 हल: यहाँ, AC और BC वृत्त के सेकेंट हैं और AB D पर स्पर्श रेखा है। अतः AE × AC = AD², खंड → खंड का क्षेत्र = क्षेत्र OACB – त्रिभुज OAB का क्षेत्र → परिधि = आर्क ACB की लंबाई,Chord की लंबाई AB, वृत्त के महत्वपूर्ण गुण, हल किए गए उदाहरण and संक्षेप: वृत्त Example, for RRB NTPC/ASM/CA/TA 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for संक्षेप: वृत्त.
Introduction of संक्षेप: वृत्त in English is available as part of our Mathematics for RRB NTPC (Hindi) for RRB NTPC/ASM/CA/TA & संक्षेप: वृत्त in Hindi for Mathematics for RRB NTPC (Hindi) course. Download more important topics related with notes, lectures and mock test series for RRB NTPC/ASM/CA/TA Exam by signing up for free. RRB NTPC/ASM/CA/TA: संक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA
Description
Full syllabus notes, lecture & questions for संक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA - RRB NTPC/ASM/CA/TA | Plus excerises question with solution to help you revise complete syllabus for Mathematics for RRB NTPC (Hindi) | Best notes, free PDF download
Information about संक्षेप: वृत्त
In this doc you can find the meaning of संक्षेप: वृत्त defined & explained in the simplest way possible. Besides explaining types of संक्षेप: वृत्त theory, EduRev gives you an ample number of questions to practice संक्षेप: वृत्त tests, examples and also practice RRB NTPC/ASM/CA/TA tests
142 videos|172 docs|185 tests
Join Course for Free
Download as PDF
Explore Courses for RRB NTPC/ASM/CA/TA exam
Related Searches

Sample Paper

,

practice quizzes

,

Summary

,

MCQs

,

past year papers

,

study material

,

Exam

,

shortcuts and tricks

,

Viva Questions

,

Free

,

pdf

,

ppt

,

संक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

,

mock tests for examination

,

संक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

,

Extra Questions

,

Previous Year Questions with Solutions

,

Semester Notes

,

Objective type Questions

,

video lectures

,

संक्षेप: वृत्त | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

,

Important questions

;
Additional Information about संक्षेप: वृत्त for RRB NTPC/ASM/CA/TA Preparation

संक्षेप: वृत्त Free PDF Download

The संक्षेप: वृत्त is an invaluable resource that delves deep into the core of the RRB NTPC/ASM/CA/TA exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the संक्षेप: वृत्त now and kickstart your journey towards success in the RRB NTPC/ASM/CA/TA exam.

Importance of संक्षेप: वृत्त

The importance of संक्षेप: वृत्त cannot be overstated, especially for RRB NTPC/ASM/CA/TA aspirants. This document holds the key to success in the RRB NTPC/ASM/CA/TA exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

संक्षेप: वृत्त Notes

संक्षेप: वृत्त Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to संक्षेप: वृत्त. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, संक्षेप: वृत्त Notes on EduRev are your ultimate resource for success.

संक्षेप: वृत्त RRB NTPC/ASM/CA/TA Questions

The "संक्षेप: वृत्त RRB NTPC/ASM/CA/TA Questions" guide is a valuable resource for all aspiring students preparing for the RRB NTPC/ASM/CA/TA exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study संक्षेप: वृत्त on the App

Students of RRB NTPC/ASM/CA/TA can study संक्षेप: वृत्त alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the संक्षेप: वृत्त, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of संक्षेप: वृत्त is prepared as per the latest RRB NTPC/ASM/CA/TA syllabus.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup