Open App

RRB NTPC/ASM/CA/TA Exam > RRB NTPC/ASM/CA/TA Notes > Mathematics for RRB NTPC (Hindi) > सारांश: बहुभुज

सारांश: बहुभुज | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

बहुभुज एक सपाट सतह पर एक आकार है जो सीधे रेखाओं के मिलकर एक क्षेत्र को घेरने से बनता है। एक बहुभुज का उदाहरण एक त्रिकोण है, जिसमें तीन भुजाएँ होती हैं। बहुभुज दो आयामों में सपाट आकार होते हैं। यह लेख गणित में बहुभुजों के सिद्धांत का अन्वेषण करता है, जिसमें त्रिकोण जैसे प्रकारों पर ध्यान केंद्रित किया गया है—समान भुजाएँ (equilateral), समकोण त्रिकोण (right-angled triangles), और विभिन्न भुजाएँ (scalene)—और चतुर्भुज जैसे समानांतर चतुर्भुज (parallelograms), आयत (rectangles), वर्ग (squares), समकोण (rhombuses), और समतल चतुर्भुज (trapeziums)। यह क्षेत्रफल, परिमाण, बाह्य कोणों का योग, और आंतरिक कोणों का योग निकालने के लिए सूत्रों पर चर्चा करता है, जो हल किए गए उदाहरणों और विस्तृत चित्रण के साथ हैं। बहुभुज क्या है?

यह एक सपाट आकार है जिसमें अनेक भुजाएँ होती हैं। प्रत्येक प्रकार का नाम उसके भुजाओं की संख्या के आधार पर होता है। उदाहरण के लिए, एक त्रिकोण (3-gon) में तीन भुजाएँ होती हैं, और एक चतुर्भुज (4-gon) में चार भुजाएँ होती हैं। भुजाओं की संख्या के आधार पर कई अन्य प्रकार भी होते हैं।

बहुभुज की परिभाषा

बहुभुज: दो-आयामी आकार जिनकी भुजाएँ और कोनों पर कोण होते हैं।
सभी 2D आकार बहुभुज नहीं हैं: जबकि बहुभुजों में भुजाएँ और कोण होते हैं, सभी 2D आकार में ऐसा नहीं होता।
भुजाओं/किनारों की परिभाषा: रेखा खंड जो एक बहुभुज की सीमाएँ बनाते हैं।
कोण/कोने: वे बिंदु जहाँ दो भुजाएँ मिलती हैं, जिससे कोण बनते हैं।
गैर-बहुभुज उदाहरण: वृत्त, जो 2D होते हैं, लेकिन भुजाओं और कोणों की कमी के कारण बहुभुज नहीं होते।

बहुभुज के प्रकार

परिभाषा से अच्छी तरह परिचित होने के बाद, आइए हम विभिन्न प्रकारों के साथ एक कदम आगे बढ़ते हैं और उनके बारे में सीखते हैं।

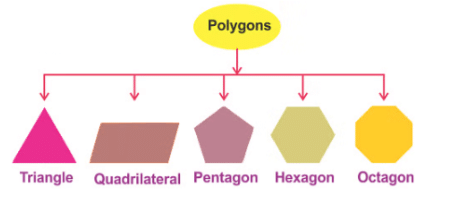
सारांश: बहुभुज | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

त्रिभुज (3 भुजाओं वाला बहुभुज)

एक त्रिभुज की एक बुनियादी विशेषता यह है कि त्रिभुज के आंतरिक कोणों का कुल योग 180 डिग्री के बराबर होता है और भुजाओं, कोणों और शीर्षों के आधार पर उन्हें निम्नलिखित प्रकारों में वर्गीकृत किया जाता है:

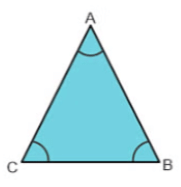
समान्तर त्रिभुज: एक त्रिभुज जिसमें सभी भुजाएँ समान होती हैं, उसे समान्तर त्रिभुज कहा जाता है। उदाहरण के लिए, ∆ABC; एक समान्तर त्रिभुज होने के लिए भुजाओं की स्थिति होनी चाहिए; AB = BC = CA, और प्रत्येक कोण 60 डिग्री के बराबर होना चाहिए, अर्थात् ∠A = ∠B = ∠C = 60°।
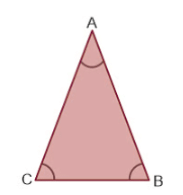
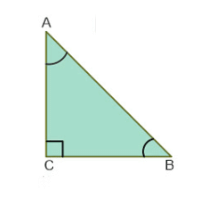
समकोण त्रिभुज: एक त्रिभुज जिसे समकोण त्रिभुज कहा जाता है, जिसमें एक कोण 90° होता है। यहाँ, ∆ABC एक समकोण त्रिभुज है क्योंकि ∠C = 90°।
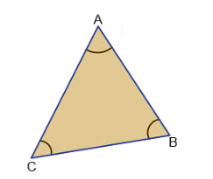
असमान त्रिभुज: एक त्रिभुज जिसकी सभी तीन भुजाएँ भिन्न या असमान होती हैं, उसे असमान त्रिभुज कहा जाता है।
समकोण त्रिभुज: एक त्रिभुज जिसमें एक कोण 90° होता है, उसे समकोण त्रिभुज कहा जाता है।

त्रिभुजों को उनके कोणों के आधार पर भी वर्गीकृत किया जा सकता है, जैसे कि तीव्र कोण त्रिभुज (जिसमें कोण 90° से कम होते हैं) और अधिमान कोण त्रिभुज (जिसमें कोण 90° से अधिक होते हैं)। इस वर्गीकरण को त्रिभुजों पर एक अलग लेख में विस्तार से कवर किया जाएगा।

चौभुज (4 भुजाओं वाला बहुभुज)

कोई भी चार गैर-कोलिनियर बिंदु एक चौभुज बनाते हैं; चौभुज का विभिन्न आकारों के आधार पर कई नाम होते हैं। नीचे कुछ महत्वपूर्ण प्रकारों पर चर्चा की गई है:

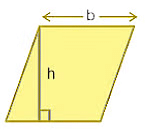
समांतर चतुर्भुज: एक समांतर चतुर्भुज में, विपरीत भुजाएँ समानांतर और समान होती हैं, और विकर्ण एक-दूसरे को आधा करते हैं। इसके अलावा, दो निकटवर्ती कोणों का योग 180 डिग्री होता है।
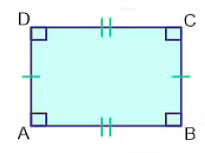
आयत: एक आयत में, विपरीत भुजाएँ समानांतर और समान होती हैं, और विकर्ण एक-दूसरे को आधा करते हैं। सभी कोण आयत में समान होते हैं और निकटवर्ती कोणों का योग 180 डिग्री के बराबर होता है।
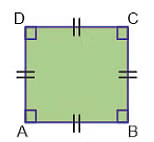
वर्ग: एक वर्ग में सभी चार भुजाएँ समान होती हैं और विपरीत भुजाएँ एक-दूसरे के समानांतर होती हैं, और विकर्ण एक-दूसरे को आधा करते हैं। इसके अलावा, सभी कोण 90 डिग्री के होते हैं।
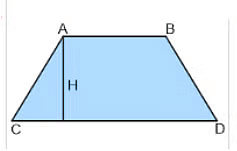
तिर्यक चतुर्भुज: एक तिर्यक चतुर्भुज में सभी भुजाएँ भिन्न लंबाई की होती हैं, इस प्रकार कि एक जोड़ी विपरीत भुजाएँ समानांतर होती हैं। तिर्यक चतुर्भुज के कोणों या विकर्णों के बारे में कुछ निश्चित नहीं होता है।

अन्य बहुभुज

कुछ अन्य महत्वपूर्ण बहुभुजों के उदाहरण निम्नलिखित हैं:

पेंटागन: एक आकृति जिसमें पांच सीधी रेखाएँ और 108 डिग्री के कोण होते हैं।
हैक्सागन: एक आकृति जिसमें छह भुजाएँ और 120 डिग्री के कोण होते हैं।
हेप्टागन: एक बहुभुज जिसमें सात भुजाएँ होती हैं।
ऑक्टागन: एक बहुभुज जिसमें आठ भुजाएँ होती हैं।
नॉनागन: एक नौ भुजाओं वाली आकृति।
डेकागन: एक बहुभुज जिसमें दस भुजाएँ होती हैं।
हेंडेकागन: एक ग्यारह भुजाओं वाली आकृति।
डोडेकागन: एक बारह भुजाओं वाली आकृति।

अब जब हम परिभाषा, प्रकार और उनके विवरण के बारे में जान चुके हैं, आइए अब उनके वर्गीकरण के बारे में सीखते हैं।

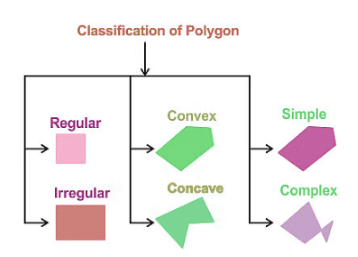
नियमित और अनियमित

नियमित बहुभुज: एक नियमित बहुभुज में सभी भुजाएँ और आंतरिक कोण समान होते हैं, जैसे कि एक समांतर चतुर्भुज, वर्ग, या समभुज त्रिकोण।
अनियमित बहुभुज: एक अनियमित बहुभुज में भुजाएँ और कोण असमान होते हैं, जैसे कि आयत, स्केलिन त्रिकोण, या पतंग।

अवकामी या अवतल

एक आकृति जिसमें सभी आंतरिक कोण 180 डिग्री से कम होते हैं, उसे अवतल बहुभुज कहा जाता है। दूसरी ओर, यदि कोई आंतरिक कोण 180 डिग्री से अधिक है, तो इसे अवकामी बहुभुज कहा जाता है।

सरल या जटिल

एक सरल प्रकार का बहुभुज केवल एक सीमा होती है, जहाँ रेखाएँ या भुजाएँ एक-दूसरे को पार नहीं करती हैं। इसके विपरीत, एक जटिल प्रकार के बहुभुज में भुजाएँ एक-दूसरे को काटती हैं।

बहुभुज सूत्र

बहुभुजों का क्षेत्रफल और परिमाप

परिमाप को किसी दो-आयामी आकृति के किनारे द्वारा घेरने वाली कुल दूरी के रूप में समझा जा सकता है। कुछ सामान्य रूप से उपयोग किए जाने वाले बहुभुजों का परिमाप नीचे सूचीबद्ध किया गया है:

त्रिकोण का परिमाप = सभी भुजाओं का कुल योग।
पैरालेलोग्राम का परिमाप = 2 × (समांतर भुजाओं की लंबाई का योग)।
वर्ग का परिमाप = 4a (a = भुजा की लंबाई)।
समांतर चतुर्भुज का परिमाप = 4x (x = भुजा की लंबाई)।
आयत का परिमाप = 2 × (L × B)।

क्षेत्रफल उस कुल स्थान को कहा जाता है जो किसी आकृति द्वारा घेर लिया जाता है। बहुभुज का क्षेत्रफल सूत्र भुजाओं की संख्या और वर्गीकरण पर निर्भर करता है। कुछ सामान्य आकृतियों के लिए क्षेत्रफल सूत्र हैं:

त्रिकोण का क्षेत्रफल = 1/2 × आधार × ऊँचाई।
पैरालेलोग्राम का क्षेत्रफल = (आधार × ऊँचाई)।
वर्ग का क्षेत्रफल = a²।
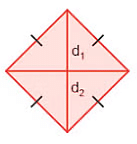
समांतर चतुर्भुज का क्षेत्रफल = 1/2 × d1 × d2। यहाँ d1 और d2 समांतर चतुर्भुज के दो विकर्णों की लंबाई हैं।
आयत का क्षेत्रफल = लंबाई × चौड़ाई।

बहुभुज में कोणों का योग

पिछले शीर्षक में, हमने विभिन्न क्षेत्रफल और परिमाण से संबंधित सूत्रों के बारे में सीखा। इसी क्रम में, चलिए हम कोणों के योग के बारे में सीखते हैं। कोणों को विभिन्न प्रकार के बहुभुजों के लिए आंतरिक कोणों और बाह्य कोणों में वर्गीकृत किया गया है।

बहुभुज के आंतरिक कोणों का योग

आंतरिक कोण, जैसा कि नाम से स्पष्ट है, वे कोण हैं जो बहुभुज के भीतर, निकटवर्ती भुजाओं के बीच बनते हैं। इन कोणों का मान नियमित बहुभुज के मामले में समान होता है।

n भुजाओं वाले नियमित बहुभुज के सभी आंतरिक कोणों का योग = (n − 2) × 180° = (n − 2)π रेडियन, जहाँ 'n' बहुभुज की भुजाओं को दर्शाता है।

एक नियमित बहुभुज के लिए प्रत्येक आंतरिक कोण = (n−2)×180°/n

बहुभुज के बाह्य कोणों का योग

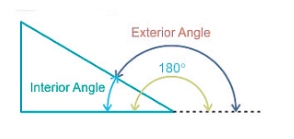
बाह्य कोण, जैसा कि नाम से स्पष्ट है, वह कोण है जो किसी दिए गए आकार की किसी भी भुजा और अगली भुजा से खींची गई रेखा (घड़ी की दिशा में या विकर्ण दिशा में) के बीच बनता है।

n भुजाओं वाले नियमित बहुभुज के लिए सभी बाह्य कोणों का योग = 360°।

इसलिए, प्रत्येक बाह्य कोण = 360°/n।

एक नियमित बहुभुज के लिए बाह्य कोण और आंतरिक कोण का संबंध = 180°।

n भुजाओं वाले नियमित बहुभुज के लिए सभी बाह्य कोणों का योग = 360°।
इसलिए, प्रत्येक बाह्य कोण = 360°/n।
एक नियमित बहुभुज के लिए बाह्य कोण और आंतरिक कोण का संबंध = 180°।

बहुभुज के हल किए गए उदाहरण

उदाहरण 1: चार भुजाओं वाला एक चतुर्भुज, सभी आंतरिक कोणों का योग क्या है?

= (4 – 2) × 180°

= 2 × 180°

एक बहुभुज के बाहरी और आंतरिक कोण को 2x और 3x मानते हैं।

2x + 3x = 180°

5x = 180°

x = 36°

बाहरी कोण = 72°

भुजाओं की संख्या = 360° / बाहरी कोण

= 360° / 72°

= 5

5 भुजाओं वाला बहुभुज पेंटागन है।

दी गई जानकारी के अनुसार:

180(n – 2) = 540

n – 2 = 3

n = 5

भुजाओं की संख्या = 5।

सूत्र के अनुसार, प्रत्येक बाहरी कोण = 360° / n

यहाँ n = भुजाओं की संख्या।

60° = 360° / n

n = 360° / 60°

n = 6

यह बहुभुज हैक्सागन है।

The document सारांश: बहुभुज | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA is a part of the RRB NTPC/ASM/CA/TA Course Mathematics for RRB NTPC (Hindi).

All you need of RRB NTPC/ASM/CA/TA at this link: RRB NTPC/ASM/CA/TA

	Mathematics for RRB NTPC (Hindi) 142 videos\|172 docs\|185 tests

Mathematics for RRB NTPC (Hindi)

142 videos|172 docs|185 tests

Join Course for Free

About this Document

Oct 18, 2025 Last updated

Related Exams

RRB NTPC/ASM/CA/TA Bank Exams SSC JE SSC CGL

Document Description: सारांश: बहुभुज for RRB NTPC/ASM/CA/TA 2025 is part of Mathematics for RRB NTPC (Hindi) preparation. The notes and questions for सारांश: बहुभुज have been prepared according to the RRB NTPC/ASM/CA/TA exam syllabus. Information about सारांश: बहुभुज covers topics like बहुभुज के प्रकार, बहुभुज में कोणों का योग, बहुभुज के हल किए गए उदाहरण and सारांश: बहुभुज Example, for RRB NTPC/ASM/CA/TA 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for सारांश: बहुभुज.

Introduction of सारांश: बहुभुज in English is available as part of our Mathematics for RRB NTPC (Hindi) for RRB NTPC/ASM/CA/TA & सारांश: बहुभुज in Hindi for Mathematics for RRB NTPC (Hindi) course. Download more important topics related with notes, lectures and mock test series for RRB NTPC/ASM/CA/TA Exam by signing up for free. RRB NTPC/ASM/CA/TA: सारांश: बहुभुज | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

Description

Full syllabus notes, lecture & questions for सारांश: बहुभुज | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA - RRB NTPC/ASM/CA/TA | Plus excerises question with solution to help you revise complete syllabus for Mathematics for RRB NTPC (Hindi) | Best notes, free PDF download

Information about सारांश: बहुभुज

In this doc you can find the meaning of सारांश: बहुभुज defined & explained in the simplest way possible. Besides explaining types of सारांश: बहुभुज theory, EduRev gives you an ample number of questions to practice सारांश: बहुभुज tests, examples and also practice RRB NTPC/ASM/CA/TA tests

	Mathematics for RRB NTPC (Hindi) 142 videos\|172 docs\|185 tests

Mathematics for RRB NTPC (Hindi)

142 videos|172 docs|185 tests

Join Course for Free

Download as PDF

Explore Courses for RRB NTPC/ASM/CA/TA exam

Semester Notes

study material

सारांश: बहुभुज | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

shortcuts and tricks

Sample Paper

Important questions

video lectures

Exam

pdf

सारांश: बहुभुज | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

practice quizzes

MCQs

Viva Questions

Extra Questions

mock tests for examination

Free

ppt

Summary

past year papers

सारांश: बहुभुज | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

Objective type Questions

Previous Year Questions with Solutions

;

Additional Information about सारांश: बहुभुज for RRB NTPC/ASM/CA/TA Preparation

सारांश: बहुभुज Free PDF Download

The सारांश: बहुभुज is an invaluable resource that delves deep into the core of the RRB NTPC/ASM/CA/TA exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the सारांश: बहुभुज now and kickstart your journey towards success in the RRB NTPC/ASM/CA/TA exam.

Importance of सारांश: बहुभुज

The importance of सारांश: बहुभुज cannot be overstated, especially for RRB NTPC/ASM/CA/TA aspirants. This document holds the key to success in the RRB NTPC/ASM/CA/TA exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

सारांश: बहुभुज Notes

सारांश: बहुभुज Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to सारांश: बहुभुज. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, सारांश: बहुभुज Notes on EduRev are your ultimate resource for success.

सारांश: बहुभुज RRB NTPC/ASM/CA/TA Questions

The "सारांश: बहुभुज RRB NTPC/ASM/CA/TA Questions" guide is a valuable resource for all aspiring students preparing for the RRB NTPC/ASM/CA/TA exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study सारांश: बहुभुज on the App

Students of RRB NTPC/ASM/CA/TA can study सारांश: बहुभुज alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the सारांश: बहुभुज, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of सारांश: बहुभुज is prepared as per the latest RRB NTPC/ASM/CA/TA syllabus.

Education Revolution

Signup to see your scores go up within 7 days!

Access 1000+ FREE Docs, Videos and Tests

Continue with Google

Takes less than 10 seconds to signup