Unit Test (Solutions): Rational Numbers | Mathematics (Maths) Class 7 (Old NCERT) PDF Download
Time: 1 hour M.M. 15
Attempt all questions.
- Question numbers 1 to 5 carry 1 mark each.
- Question numbers 6 to 10 carry 2 marks each.
Q1: List any five rational numbers between -1/2 and 2/3 (1 mark)
Ans: The five rational numbers present between -1/2 and 2/3 are,
-1/2 < (less than) (-1/6) < (0) < (1/3) < (1/2) < (20/36) < 2/3
Q2: Give any four rational numbers equivalent to 4/9 (1 mark)
Ans: The four rational numbers present which are equivalent to the fraction 5/-3 are,
= (4 × 2)/ (9 × 2), (4 × 3)/ (9 × 3), (4 × 4)/ (9 × 4) and (4 × 5)/ (9× 5)
= 8/18, 12/27, 16/36 and 20/45
Q3: Rewrite -8/6 in the simplest form: (1 mark)
Ans: The given above rational numbers can be simplified further,
Then,
= -4/3 … [∵ Divide both the numerator and denominator by 2]
Q4: Which of these following pairs represents the same rational number? (1 mark)
(i) (-7/21) and (3/9)
(ii) (-16/20) and (20/-25)
(iii) (-5/-9) and (5/-9)
(iv) All of the above
Ans: (ii) (-16/20) and (20/-25)
Solution: We have to check whether the given pair represents the same rational number.
Then,
-16/20 = 20/-25
-4/5 = 4/-5
∵ -4/5 = -4/5
Hence -16/20 = 20/-25
So, the given pair represents the same rational number.
Q5: Which is the correct option in the following: (1 mark)
(i) (-5/6) > (-4/3)
(ii) (-5/6) = (-4/3)
(iii) (-5/6) < (-4/3)
(ii) None of the above
Ans: (i) (-5/6) > (-4/3)
The LCM of the denominators of 6 and 3 is 6
∴ (-5/6) = [(-5 × 1)/ (6 × 1)] is = (-5/6)
And (-4/3) = [(-4 × 2)/ (3 × 2)] equals to (-12/6)
Now,
-5 > -12
So, (-5/6) > (- 12/6)
∴ -5/6 > -12/6
Hence, – 5/6 is greater.
Q6: Find (2 marks)
(a) 5/18 - 11/30
Ans:
Take the LCM of these denominators of the above-given rational numbers.
LCM of the numbers 18 and 30 is 90
Express each of these given rational numbers with the above LCM, by taking it as the common denominator.
Now,
(5/18) is equal to [(5×5)/(18×5)] = (25/90)
(11/30) equals to [(11×3)/(30×3)] = (33/90)
Then,
= (25/90) - (33/90) ... [the denominator is same in both the rational numbers]
= (25 - 33)/90
= (-8/90)
= (-4/45)
(b) 7/45 - (-4/12)
Ans:
We can also write that -(-4/12) = 4/12
= 7/45 + 4/12
Now, take the LCM of the denominators of the above given rational numbers.
LCM of the numbers 45 and 12 is 180
Express each of these given rational numbers with the above LCM, by taking it as the common denominator.
Now,
(7/45) = [(7×4)/(45×4)] = (28/180)
(4/12) = [(4×15)/(12×15)] = (60/180)
Then,
= (28/180) + (60/180) ... [the denominator is the same in both the rational numbers]
= (28 + 60)/180
= 88/180
= 44/90
= 22/45
Q7: Find the value of: (2 marks)
(a) (-3/10) ÷ 2/5
Ans:
We have,
= (-3/10) × (5/2) … [the reciprocal of the fraction (2/5) is (5/2)]
The product of these two rational numbers is equal to = (product of their numerator) / (product of their denominator)
= (-3×5) / (10×2)
= (-15) / (20)
= (-3) / (4)
(b) (-5/9) ÷ 2/3
Ans:
We have,
= (-5/9) × (3/2) … [since the reciprocal of (2/3) is (3/2)]
The product of the following two rational numbers is equal to = (product of their numerator) / (product of their denominator)
= (-5×3) / (9×2)
= -15/18
= -5/6
Q8: Find the given product: (2 marks)
(a) (8/5) × (-3/7)
Ans:
The product of the two rational numbers is equal to = (product of their numerator) divided by (product of their denominator)
The above question can also be written as (8/5) × (-3/7)
We have,
= (8×-3) / (5×7)
= -24/35
(b) (6/8) × (-5)
Ans:
The product of two rational numbers is equal to (product of their numerator) divided by (product of their denominator)
The above question can also be written as (6/8) × (-5/1)
We have,
= (6×-5) / (8×1)
= -30/8
= -15/4
Q9: Which of these following pairs represents the same rational number? (2 marks)
(i) (-7/21) and (3/9)
Ans:
We have to check whether the given pair represents the same rational number.
Then,
-7/21 = 3/9
-1/3 = 1/3
∵ -1/3 ≠ 1/3
Hence -7/21 ≠ 3/9
So, the given pair does not represent the same rational number.
(ii) (-16/20) and (20/-25)
Ans: We have to check whether the given pair represents the same rational number.
Then,
-16/20 = 20/-25
-4/5 = 4/-5
∵ -4/5 = -4/5
Hence -16/20 = 20/-25
So, the given pair represents the same rational number.
Q10: Represent these numbers on the number line. (2 marks)
(i) 7/4
(ii) -5/6
Ans: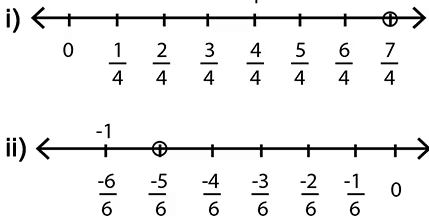
|
76 videos|386 docs|39 tests
|
FAQs on Unit Test (Solutions): Rational Numbers - Mathematics (Maths) Class 7 (Old NCERT)
| 1. What are rational numbers and how are they represented? |  |
| 2. How do you add and subtract rational numbers? |  |
| 3. Can you explain how to multiply and divide rational numbers? |  |
| 4. What is the difference between proper and improper fractions? |  |
| 5. How can you convert a decimal to a rational number? |  |
















