IEEE Standard 754 Floating Point Numbers | Digital Circuits - Electronics and Communication Engineering (ECE) PDF Download
IEEE 754 is a standard way to represent and work with decimal numbers (like 3.14 or -0.5) on computers. It was created in 1985 by a group called the Institute of Electrical and Electronics Engineers (IEEE) to solve problems with older, inconsistent methods that made it hard to get reliable results across different computers.
Today, it’s the most widely used system for handling these kinds of numbers on devices like PCs, Macs, and Unix-based systems. IEEE 754 represents floating-point numbers using three main parts:
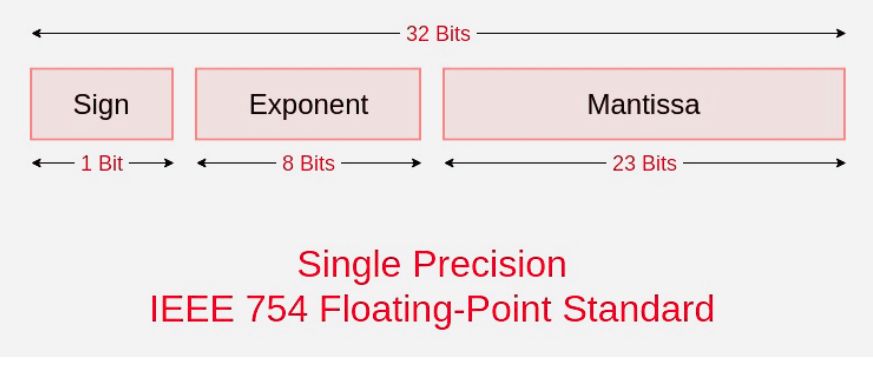
- Sign: This just shows if the number is positive (0) or negative (1).
- Exponent: This part controls the size of the number (how big or small it is). To handle both large and small values, a fixed "bias" is added to the actual exponent so it can be stored properly.
- Mantissa: This is the core part of the number—its significant digits. In this system, it’s "normalized," meaning it’s written with a single 1 before the decimal point, followed by the rest of the digits (using only 0s and 1s).
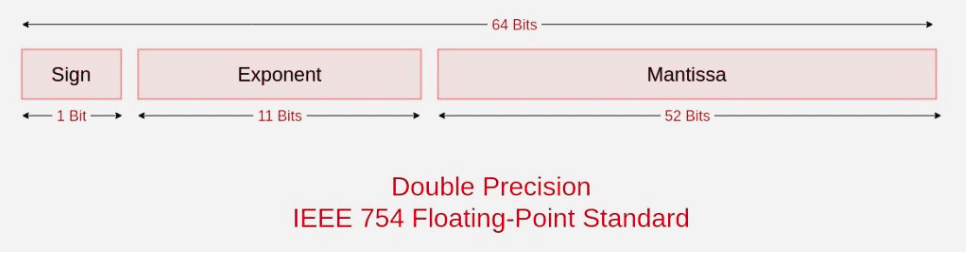
IEEE 754 numbers are divided into two based on the above three components: single precision and double precision.

Example:
85.125
85 = 1010101
0.125 = 001
85.125 = 1010101.001
=1.010101001 x 2^6
sign = 0
1. Single precision:
biased exponent 127+6=133
133 = 10000101
Normalised mantisa = 010101001
we will add 0's to complete the 23 bits
The IEEE 754 Single precision is:
= 0 10000101 01010100100000000000000
This can be written in hexadecimal form 42AA4000
2. Double precision:
biased exponent 1023+6=1029
1029 = 10000000101
Normalised mantisa = 010101001
we will add 0's to complete the 52 bits
The IEEE 754 Double precision is:
= 0 10000000101 0101010010000000000000000000000000000000000000000000
This can be written in hexadecimal form 4055480000000000
Special Values: IEEE has reserved some values that can ambiguity.
- Zero: Zero is a special value denoted with an exponent and mantissa of 0. -0 and +0 are distinct values, though they both are equal.
- Denormalised: If the exponent is all zeros, but the mantissa is not then the value is a denormalized number. This means this number does not have an assumed leading one before the binary point.
- Infinity : The values +infinity and -infinity are denoted with an exponent of all ones and a mantissa of all zeros. The sign bit distinguishes between negative infinity and positive infinity. Operations with infinite values are well defined in IEEE.
- Not A Number (NAN) : The value NAN is used to represent a value that is an error. This is represented when exponent field is all ones with a zero sign bit or a mantissa that it not 1 followed by zeros. This is a special value that might be used to denote a variable that doesn’t yet hold a value.
| EXPONENT | MANTISA | VALUE |
|---|---|---|
| 0 | 0 | exact 0 |
| 255 | 0 | Infinity |
| 0 | not 0 | denormalised |
| 255 | not 0 | Not a number (NAN) |
Similar for Double precision (just replacing 255 by 2049), Ranges of Floating point numbers:

The range of positive floating point numbers can be split into normalized numbers, and denormalized numbers which use only a portion of the fractions’s precision. Since every floating-point number has a corresponding, negated value, the ranges above are symmetric around zero.
There are five distinct numerical ranges that single-precision floating-point numbers are not able to represent with the scheme presented so far:
- Negative numbers less than – (2 – 2-23) × 2127 (negative overflow)
- Negative numbers greater than – 2-149 (negative underflow)
- Zero
- Positive numbers less than 2-149 (positive underflow)
- Positive numbers greater than (2 – 2-23) × 2127 (positive overflow)
Overflow generally means that values have grown too large to be represented. Underflow is a less serious problem because is just denotes a loss of precision, which is guaranteed to be closely approximated by zero.
Table of the total effective range of finite IEEE floating-point numbers is shown below:

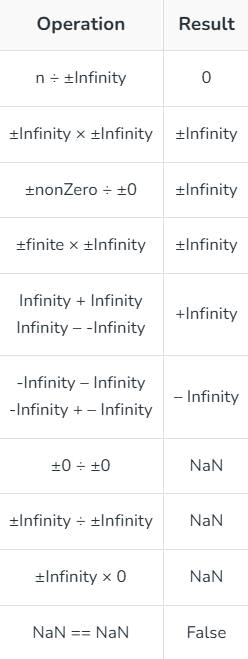
Special Operations:
|
75 videos|188 docs|70 tests
|
FAQs on IEEE Standard 754 Floating Point Numbers - Digital Circuits - Electronics and Communication Engineering (ECE)
| 1. What is IEEE Standard 754 for Floating Point Numbers? |  |
| 2. What are the main components of a floating-point representation according to IEEE 754? |  |
| 3. How does rounding work in IEEE 754 floating-point arithmetic? |  |
| 4. What are the common exceptions defined by IEEE 754? |  |
| 5. Why is IEEE 754 important in computer programming and engineering? |  |





















