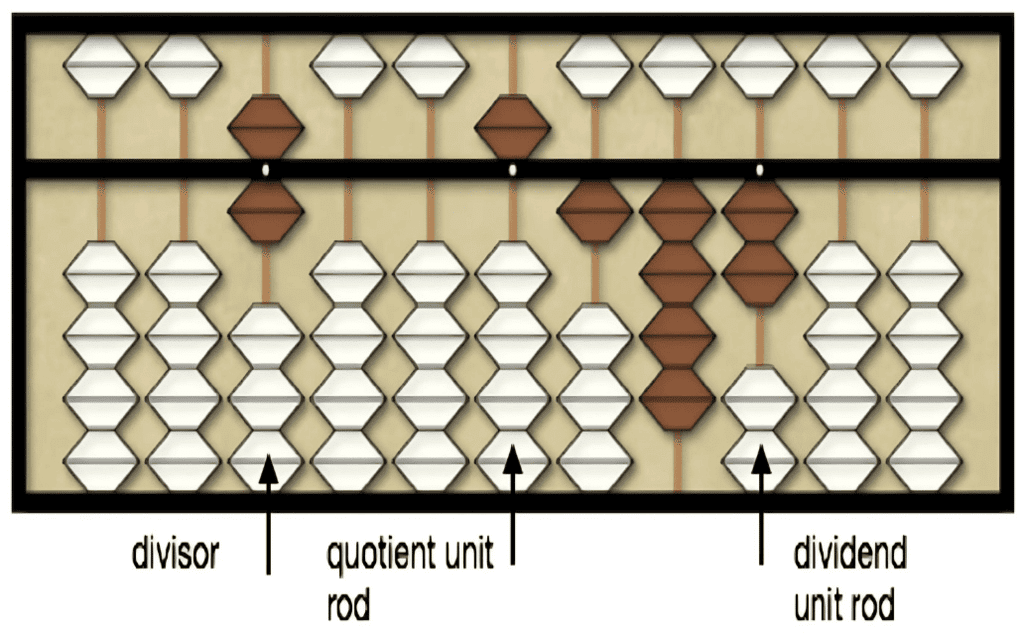
Setting Up:
First, place the number you want to divide (called the dividend) on the right side of the abacus, and the number you are dividing by (called the divisor) on the left side.
Leave four empty rods between these numbers to work out the answer (called the quotient).
Division Steps:
Find the Starting Point:
Look for where the first few beads on the abacus make a number equal to or bigger than the divisor.
These beads are our working digits.
Guess and Check:
Guess a number that, when multiplied by the divisor, is less than or equal to our working digits.
Place this guess in the quotient area on the abacus.
Multiply and Subtract:
Multiply the divisor by your guess and subtract this from the working digits.
The beads left are the remainder.
Bring Down More Beads:
Bring down the next bead (digit) from the dividend to add to the remainder.
This new number is your new set of working digits.
Repeat:
Keep doing this: guessing, multiplying, and subtracting until you have worked through all the beads of the dividend.
If there's a gap with no beads in the quotient, put zero beads there.
Example with Steps:
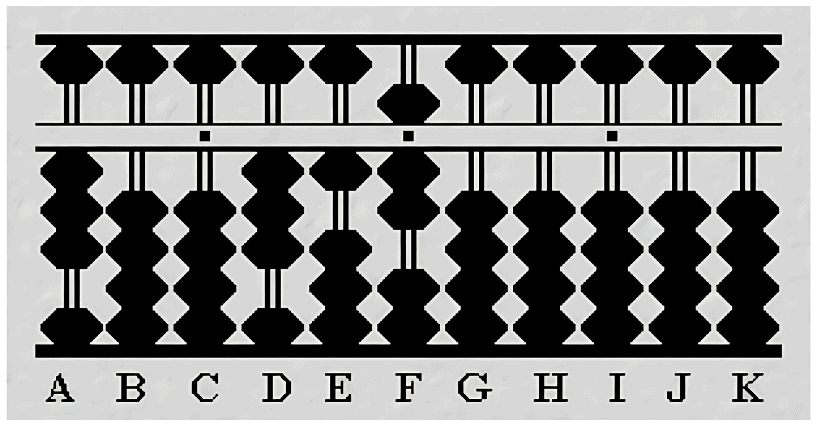
Divide 951 by 3 on the abacus:
Step 1: Set Up the Numbers
Dividend Setup: Place 951 on rods F, G, and H:
Rod F: 9 beads for 900.
Rod G: 5 beads for 50.
Rod H: 1 bead for 1.
Divisor Setup: Set 3 on rod A.
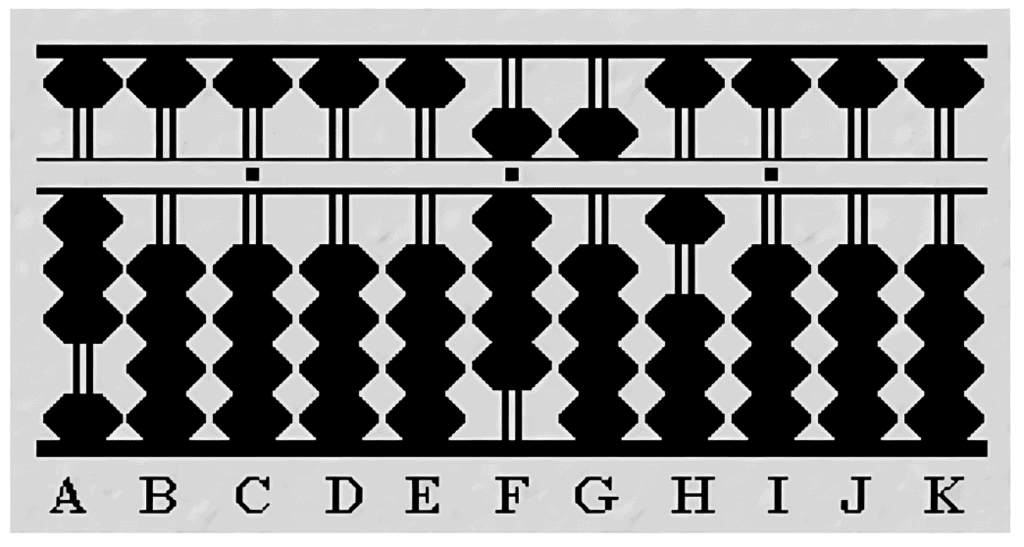
Step 2: First Division
Calculate Quotient: Compare the divisor on A (3) with the first digit on F (9). Fit three 3s into 9. Place quotient 3 on rod D.
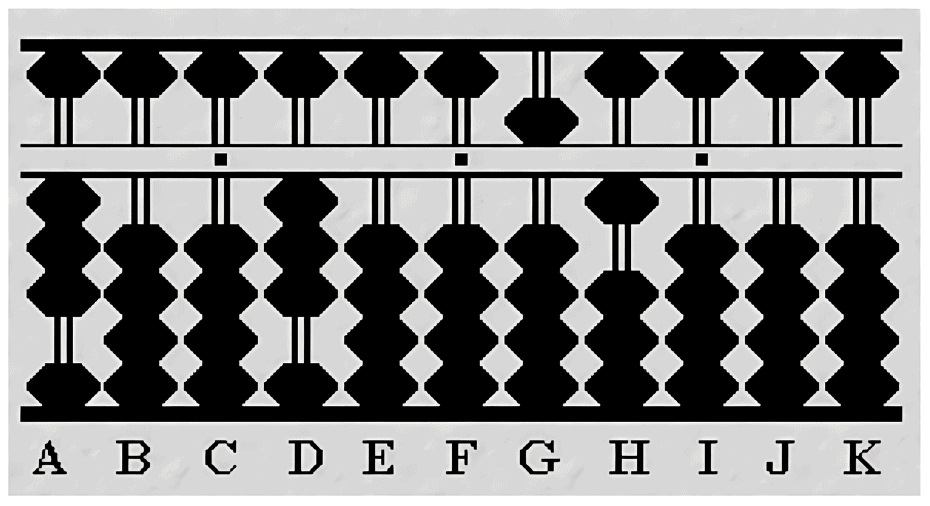
Step 3: Multiply and Subtract
Operation: Multiply divisor 3 by quotient 3 (3 x 3 = 9). Subtract 9 from rod F, resetting it to 0.
Step 4: Bring Down Next Number
Update Dividend: Bring down the next digits, making 51 on rods G and H.
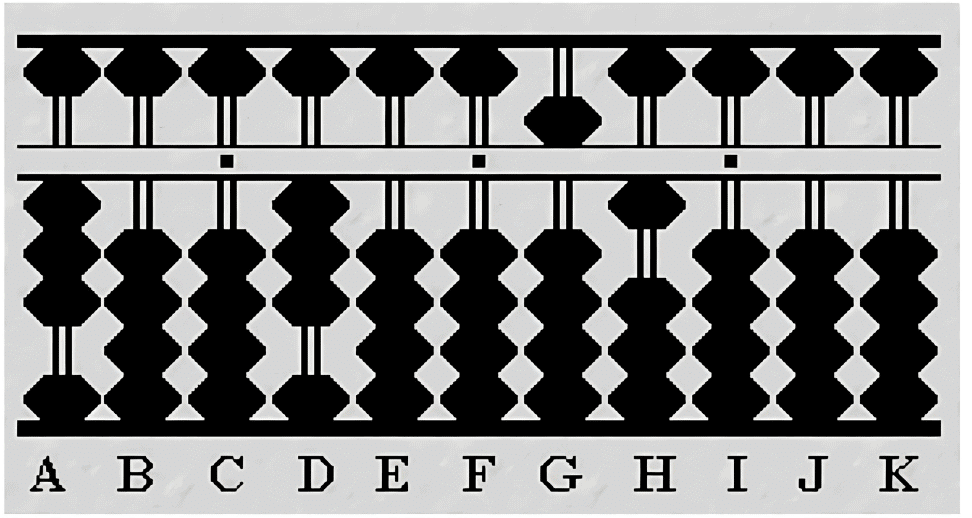
Step 5: Second Division
Calculate Quotient: For 51, divide by 3. Place 1 on rod E (3 goes into 5 once, giving 3). Subtract 3 from rod G, leaving 2.
Step 6: Final Division
Complete Operation: Consider remainder 21. Divide by 3 to place 7 on rod F. Multiply 7 by 3, and subtract from 21, clearing rods G and H.
Conclusion:
Using an abacus for division is not just about getting the right answer; it’s about understanding the process of dividing large numbers step-by-step, which helps strengthen your math skills and understanding. Just like solving puzzles, each step builds on the previous one until you see the whole picture or, in this case, the whole number!