Open App

RRB NTPC/ASM/CA/TA Exam > RRB NTPC/ASM/CA/TA Notes > Mathematics for RRB NTPC (Hindi) > अंक योग विधि: वैदिक गणित

अंक योग विधि: वैदिक गणित | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

परिचय

इस अध्याय में, हम अंक-योग विधि का अध्ययन करेंगे। यह विधि त्वरित गणना के लिए नहीं, बल्कि उत्तरों की त्वरित जांच के लिए उपयोग की जाती है। यह हमें किसी विशेष प्रश्न के लिए प्राप्त उत्तर की सत्यता की पुष्टि करने में मदद करेगी। यह तकनीक प्रतियोगी परीक्षाएं देने वाले छात्रों के लिए शानदार विभिन्न अनुप्रयोग प्रदान करती है क्योंकि उन्हें हर उत्तर के लिए पहले से चार विकल्प दिए जाते हैं। हालाँकि, अंक-योग विधि की चर्चा जगद्गुरु भारती कृष्ण महाराज द्वारा की गई है, लेकिन दुनिया के अन्य हिस्सों के गणितज्ञ इस सिद्धांत से स्वामीजी के शोध पत्र के प्रकाशन से पहले ही परिचित थे। प्रोफेसर जैकव ट्रेक्टेनबर्ग और अन्य गणितज्ञों ने अपने शोध कार्य में इस सिद्धांत पर चर्चा की है।

उदाहरण

उदाहरण 1: 2467539 का अंक-योग ज्ञात करें

उत्तर: संख्या 2467539 है। हम उस संख्या के सभी अंकों को जोड़ते हैं। 2 + 4 + 6 + 7 + 5 + 3 + 9 = 36 अब, हम संख्या 36 लेते हैं और इसके अंकों को जोड़ते हैं 3 + 6 = 9। इस प्रकार, हमने संख्या 2467539 को इसके अंक-योग 9 में परिवर्तित कर दिया है।

उदाहरण 2: 56768439 का अंक-योग ज्ञात करें

उत्तर: 5 + 6 + 7 + 6 + 8 + 4 + 3 + 9 = 48 4 + 8 = 12 1 + 2 = 3 इस प्रकार, 56768439 का अंक-योग 3 है।

उत्तर:

नोट: अंक-योग हमेशा एकल अंक होगा। आपको तब तक संख्याओं को जोड़ते रहना होगा जब तक आप एकल अंकीय उत्तर प्राप्त न कर लें।

नोट:

कुछ और उदाहरण नीचे दिए गए हैं

अंक योग विधि: वैदिक गणित | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

हमने एक संख्या के अंक-योग को कैसे गणना करें, इस पर चर्चा की है। अब हम विभिन्न अंकगणितीय क्रियाओं से जुड़े विभिन्न उदाहरणों को हल करेंगे।

उदाहरण 1: (गुणन)

प्रश्न: क्या 467532 को 107777 से गुणा करने पर 50389196364 प्राप्त होता है, यह सत्यापित करें।

उत्तर: चरण 1: पहले हम गुणन के अंश का अंक-योग निकालेंगे। चरण 2: हम गुणक का अंक-योग निकालेंगे। चरण 3: हम प्राप्त दो अंक-योगों को गुणा करेंगे। चरण 4: यदि अंतिम उत्तर उत्पाद के अंक-योग के बराबर है, तो हम अपने उत्तर को सही मान सकते हैं। 467532 का अंक-योग 9 है। 107777 का अंक-योग 2 है। जब हम 9 को 2 से गुणा करते हैं, तो उत्तर 18 आता है। फिर 18 का अंक-योग 9 है। इस प्रकार, पूर्ण गुणन प्रक्रिया का अंक-योग 9 है। अब, हम उत्पाद के अंक-योग की जांच करेंगे। 50389196364 का अंक-योग भी 9 है। प्रश्न का अंक-योग उत्तर के अंक-योग के बराबर है और इसलिए हम मान सकते हैं कि उत्पाद सही है।

उत्तर:

उदाहरण 2: (भाग)

प्रश्न: क्या 2308682040 को 36524 से भाग देने पर 63210 प्राप्त होता है, यह सत्यापित करें।

उत्तर: हम उस सूत्र का उपयोग कर सकते हैं जो हमने स्कूल में सीखा था। भागफल = भाज्य ÷ भाजक + शेषफल। इस मामले में हम उसी सूत्र का उपयोग करेंगे, लेकिन वास्तविक उत्तर के बजाय हम उनके अंक-योग का उपयोग करेंगे। भाज्य का अंक-योग 6 है। भाजक, भागफल और शेषफल का अंक-योग क्रमशः 2, 3 और 0 है। चूंकि 6 = 2 × 3 + 0, हम अपने उत्तर को सही मान सकते हैं। इस प्रकार, हम अन्य क्रियाओं से जुड़े प्रश्नों को भी हल कर सकते हैं। हालाँकि, आगे बढ़ने से पहले मैं इस विधि के लिए एक और शॉर्टकट पेश करूंगा। नियम कहता है: जब आप किसी संख्या का अंक-योग निकाल रहे हों, तो आप सभी 9 और सभी अंकों को हटा सकते हैं जो 9 में जोड़ते हैं। जब आप सभी 9 और सभी अंकों को हटा देते हैं जो 9 में जोड़ते हैं, तो आप किसी भी संख्या का अंक-योग बहुत तेज़ी से निकाल सकते हैं। हटाने का अंतिम परिणाम पर कोई प्रभाव नहीं पड़ेगा।

उत्तर:

उदाहरण लेते हैं

प्रश्न: 6372819923 का अंक-योग ज्ञात करें।

उत्तर: 6372819923 का अंक-योग है: 6 + 3 + 7 + 2 + 8 + 1 + 9 + 9 + 2 + 3 = 50 और फिर 5 + 0 = 5। अब, हम उन संख्याओं को हटा देंगे जो 9 जोड़ती हैं (6 और 3, 7 और 2, 8 और 1 और साथ ही दो 9 को भी हटा देंगे)। हमें 2 और 3 के अंक मिलते हैं जो भी 5 जोड़ते हैं। इसलिए, यह सिद्ध होता है कि हम अंक-योग की गणना के लिए संक्षिप्त विधि का उपयोग कर सकते हैं। उत्तर दोनों ही मामलों में समान होगा।

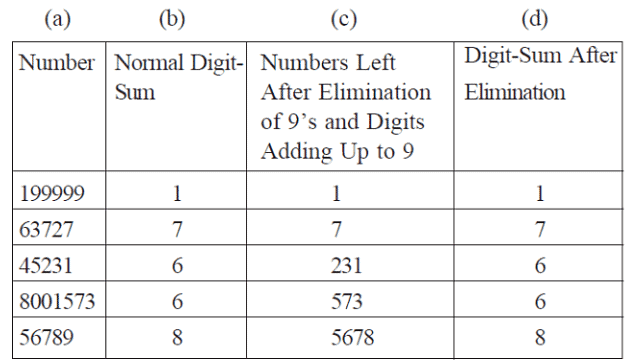
अंक योग विधि: वैदिक गणित | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

उपरोक्त तालिका से हम देख सकते हैं कि कॉलम (b) में मान और कॉलम (d) में मान समान हैं।

नोट: यदि किसी संख्या का अंक-योग 9 है, तो हम 9 को सीधे हटा सकते हैं और अंक-योग 0 हो जाता है।

उदाहरण 3: (गुणा)

प्रश्न: जाँच करें कि क्या 999816 को 727235 से गुणा करने पर 727101188760 प्राप्त होता है।

उत्तर: 999816 का अंक-योग तुरंत तीन 9 को हटाकर और 8 और 1 के संयोजन को हटाकर ज्ञात किया जा सकता है। शेष अंक 6 है (जो हमारा अंक-योग बनता है)। 727235 का अंक-योग तुरंत उन संख्याओं को हटाकर ज्ञात किया जा सकता है जो 9 जोड़ती हैं। शेष अंकों का अंक-योग 8 है। जब 8 को 6 से गुणा किया जाता है तो उत्तर 48 है और 48 का अंक-योग 3 है। लेकिन, 727101188750 का अंक-योग 2 है। प्रश्न का अंक-योग उत्तर के अंक-योग से मेल नहीं खाता है और इसलिए उत्तर निश्चित रूप से गलत है।

उदाहरण 4: (जोड़ना)

प्रश्न: जाँच करें कि क्या 18273645, 9988888, 6300852 और 11111111 का योग 45674496 है।

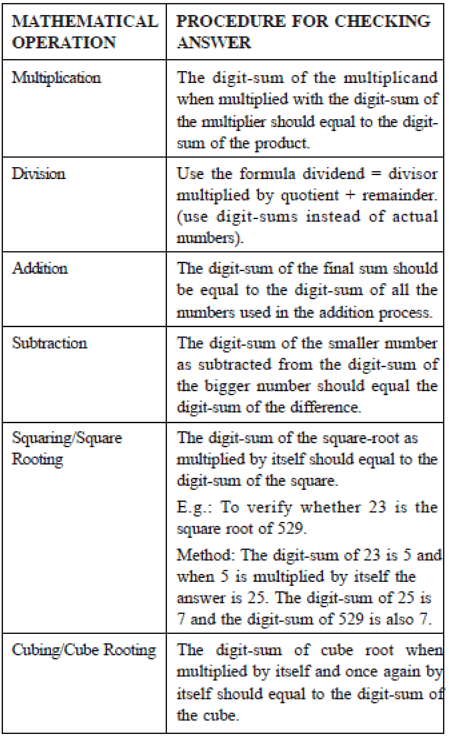
उत्तर: संख्याओं का अंक-योग क्रमशः 0, 4, 6 और 8 है। इन चारों अंक-योग का योग 18 है और 18 का अंक-योग 9 है। 45674496 का अंक-योग भी 9 है और इसलिए योग सही है। मुझे लगता है कि चार उदाहरण पर्याप्त होंगे। इसी तरह, हम अन्य गणितीय क्रियाओं द्वारा प्राप्त उत्तर की भी जांच कर सकते हैं। मैंने नीचे एक विशेष समस्या में शामिल गणितीय प्रक्रियाओं और अंक-योग की गणना की तकनीक की एक सूची दी है।

अंक योग विधि: वैदिक गणित | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

The document अंक योग विधि: वैदिक गणित | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA is a part of the RRB NTPC/ASM/CA/TA Course Mathematics for RRB NTPC (Hindi).

All you need of RRB NTPC/ASM/CA/TA at this link: RRB NTPC/ASM/CA/TA

	Mathematics for RRB NTPC (Hindi) 142 videos\|172 docs\|185 tests

Mathematics for RRB NTPC (Hindi)

142 videos|172 docs|185 tests

Join Course for Free

FAQs on अंक योग विधि: वैदिक गणित - Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

1. अंक योग विधि क्या है और यह कैसे काम करती है?

Ans. अंक योग विधि, जिसे वैदिक गणित का एक महत्वपूर्ण भाग माना जाता है, में संख्याओं को जोड़ने के लिए विशेष तकनीकों का उपयोग किया जाता है। यह विधि संख्याओं को सरलता से जोड़ने में मदद करती है, जिससे गणना तेज और सटीक होती है। इस विधि में, संख्याओं को उनकी अंकों के योग के माध्यम से जोड़ने का तरीका अपनाया जाता है, जिससे जटिल जोड़ को आसान बनाया जाता है।

2. वैदिक गणित के लाभ क्या हैं?

Ans. वैदिक गणित के कई लाभ हैं, जैसे कि गणना की गति में वृद्धि, मानसिक गणना की क्षमता में सुधार, और गणितीय समस्याओं को हल करने के लिए सरल और प्रभावी विधियों का उपयोग। इसके अलावा, यह छात्रों को गणित से नफरत करने के बजाय इसे सीखने में रुचि रखने में मदद करता है।

3. क्या अंक योग विधि का उपयोग केवल स्कूलों में किया जाता है?

Ans. नहीं, अंक योग विधि का उपयोग केवल स्कूलों में ही नहीं, बल्कि प्रतियोगी परीक्षाओं, वित्तीय गणनाओं, और दैनिक जीवन में भी किया जाता है। यह विधि किसी भी स्थान पर उपयोगी है जहाँ तेज़ और सटीक गणना की आवश्यकता होती है।

4. क्या अंक योग विधि को सीखना कठिन है?

Ans. अंक योग विधि को सीखना कठिन नहीं है, विशेष रूप से यदि व्यक्ति इसे नियमित रूप से अभ्यास करता है। कुछ सरल तकनीकों और अभ्यास के माध्यम से, कोई भी व्यक्ति इसे आसानी से समझ सकता है और अपने गणितीय कौशल को बढ़ा सकता है।

5. क्या अंक योग विधि का कोई उदाहरण दिया जा सकता है?

Ans. हाँ, उदाहरण के लिए, यदि हमें 27 और 45 का योग निकालना है, तो हम पहले अंकों को जोड़ सकते हैं: 2 + 7 = 9 और 4 + 5 = 9। फिर, हम 9 + 9 = 18 का योग करते हैं। इस प्रकार, 27 + 45 = 72 होता है। इस विधि से गणना करना सरल और तेज होता है।

About this Document

4.86/5 Rating

Oct 18, 2025 Last updated

Related Exams

RRB NTPC/ASM/CA/TA Bank Exams SSC JE SSC CGL

Document Description: अंक योग विधि: वैदिक गणित for RRB NTPC/ASM/CA/TA 2025 is part of Mathematics for RRB NTPC (Hindi) preparation. The notes and questions for अंक योग विधि: वैदिक गणित have been prepared according to the RRB NTPC/ASM/CA/TA exam syllabus. Information about अंक योग विधि: वैदिक गणित covers topics like परिचय, उदाहरण and अंक योग विधि: वैदिक गणित Example, for RRB NTPC/ASM/CA/TA 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for अंक योग विधि: वैदिक गणित.

Introduction of अंक योग विधि: वैदिक गणित in English is available as part of our Mathematics for RRB NTPC (Hindi) for RRB NTPC/ASM/CA/TA & अंक योग विधि: वैदिक गणित in Hindi for Mathematics for RRB NTPC (Hindi) course. Download more important topics related with notes, lectures and mock test series for RRB NTPC/ASM/CA/TA Exam by signing up for free. RRB NTPC/ASM/CA/TA: अंक योग विधि: वैदिक गणित | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

Description

Full syllabus notes, lecture & questions for अंक योग विधि: वैदिक गणित | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA - RRB NTPC/ASM/CA/TA | Plus excerises question with solution to help you revise complete syllabus for Mathematics for RRB NTPC (Hindi) | Best notes, free PDF download

Information about अंक योग विधि: वैदिक गणित

In this doc you can find the meaning of अंक योग विधि: वैदिक गणित defined & explained in the simplest way possible. Besides explaining types of अंक योग विधि: वैदिक गणित theory, EduRev gives you an ample number of questions to practice अंक योग विधि: वैदिक गणित tests, examples and also practice RRB NTPC/ASM/CA/TA tests

	Mathematics for RRB NTPC (Hindi) 142 videos\|172 docs\|185 tests

Mathematics for RRB NTPC (Hindi)

142 videos|172 docs|185 tests

Join Course for Free

Download as PDF

Explore Courses for RRB NTPC/ASM/CA/TA exam

अंक योग विधि: वैदिक गणित | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

shortcuts and tricks

Objective type Questions

Free

mock tests for examination

Viva Questions

Extra Questions

Exam

Summary

MCQs

past year papers

study material

Sample Paper

pdf

Important questions

Semester Notes

अंक योग विधि: वैदिक गणित | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA

ppt

video lectures

Previous Year Questions with Solutions

practice quizzes

;

Additional Information about अंक योग विधि: वैदिक गणित for RRB NTPC/ASM/CA/TA Preparation

अंक योग विधि: वैदिक गणित Free PDF Download

The अंक योग विधि: वैदिक गणित is an invaluable resource that delves deep into the core of the RRB NTPC/ASM/CA/TA exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the अंक योग विधि: वैदिक गणित now and kickstart your journey towards success in the RRB NTPC/ASM/CA/TA exam.

Importance of अंक योग विधि: वैदिक गणित

The importance of अंक योग विधि: वैदिक गणित cannot be overstated, especially for RRB NTPC/ASM/CA/TA aspirants. This document holds the key to success in the RRB NTPC/ASM/CA/TA exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

अंक योग विधि: वैदिक गणित Notes

अंक योग विधि: वैदिक गणित Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to अंक योग विधि: वैदिक गणित. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, अंक योग विधि: वैदिक गणित Notes on EduRev are your ultimate resource for success.

अंक योग विधि: वैदिक गणित RRB NTPC/ASM/CA/TA Questions

The "अंक योग विधि: वैदिक गणित RRB NTPC/ASM/CA/TA Questions" guide is a valuable resource for all aspiring students preparing for the RRB NTPC/ASM/CA/TA exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study अंक योग विधि: वैदिक गणित on the App

Students of RRB NTPC/ASM/CA/TA can study अंक योग विधि: वैदिक गणित alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the अंक योग विधि: वैदिक गणित, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of अंक योग विधि: वैदिक गणित is prepared as per the latest RRB NTPC/ASM/CA/TA syllabus.

Education Revolution