Numerical Problems: Motion in a Plane | Physics Class 11 - NEET PDF Download
Q1. What is the angle between two forces of 2N and 3N having resultant as 4N?
Sol: Using the equation R = √(A2 + B2 + 2AB cos θ)
We can write,
⇒ 4 = √(22 + 32 + 2 × 2 × 3 cos θ)
⇒ 16 = 4 + 9 + 12 cos θ
⇒ 12 cos θ = 16 - 4 - 9
⇒ 12 cos θ = 3
⇒ cos θ = 3 / 12
⇒ cos θ = cos-1(0.25)
⇒ θ = 75'32', which is the required angle.
Q2. What is the angle of projection at which horizontal range and maximum height are equal?
Sol: We can write,
u2 sin 2θ / g = R (Horizontal Range)
Therefore, we can write,
sin 2θ = 2 sin θ Cos θ
u2 sin2 θ / 2g = Hmax (Maximum Height)
⇒ 2 sin θ cos θ = 1/2 sin2 θ
⇒ tan θ = 4
⇒ θ = 75.96°, which is the required angle of projection.
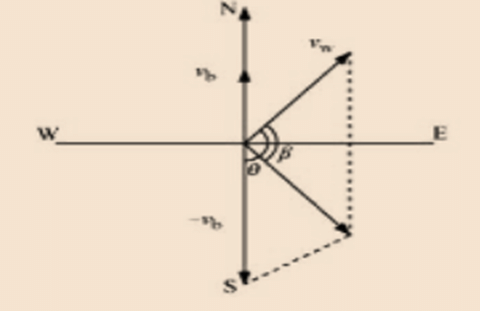
Q3. Two forces 5 kgwt and 10 kgwt are acting with an inclination of 120° between them. What is the angle which the resultant makes with 10 kgwt?
Sol: Let the angle between the forces be θ = 120∘.
Let β be the angle made by the resultant with the 10 kgwt force.
For the angle with the force P when the other force is Q: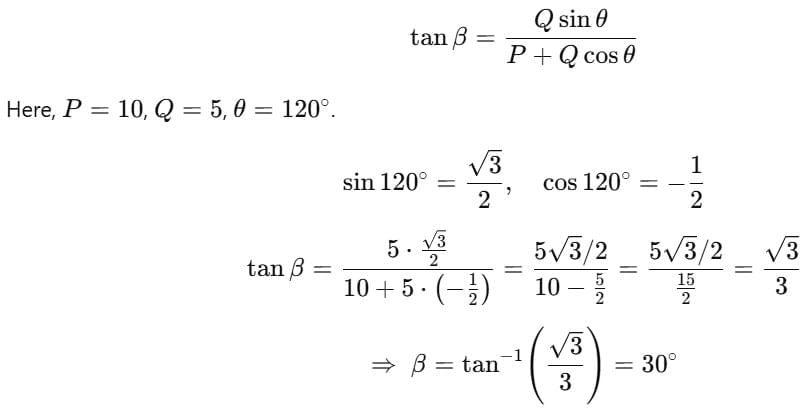
Q4. Find a unit vector parallel to the resultant of the vectors A = 2i + 3j + 4k and B = 3i + 5j + k.
Sol: 
Q5. A body of mass m is thrown with velocity u at an angle of 30° to the horizontal and another body B of the same mass is thrown with velocity at an angle of 60° to the horizontal. Find the ratio of the horizontal range and maximum height of A and B?
Sol: Case 1:
When θ = 30°
RA = (u2 / g) × sin 2(30°)
⇒ RA = (u2 / g) × √3 / 2
When θ = 60°
RB = (u2 / g) × sin 2(60°)
⇒ RB = (u2 / g) × √3 / 2
⇒ RA : RB = 1:1
Case 2:
When θ = 30°
HA = (u2 / g) × sin2 30°
⇒ HA = (u2 / g) (1 / 4)
When θ = 60°
HB = (u2 / g) × sin2 60°
⇒ HB = (u2 / g) (3 / 4)
⇒ HA : HB = 1:3, which is the required ratio.
Q6. A passenger arriving in a new town wishes to go from the station to a hotel located 10km away on a straight road from the station. A dishonest cabman takes him along a circuitous path 23km long and reaches the hotel in 28min. What is the average speed of the taxi?
Sol: Given that,
Total distance travelled can be given as = 23km
Total time taken can be given as = 28min = 28 / 60 h
Average speed of the taxi = Total distance travelled / Total time taken
⇒ Average speed of the taxi = 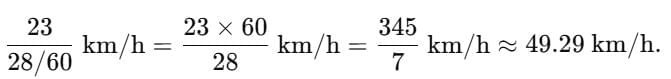
Q7. An aircraft is flying at a height of 3400m above the ground. If the angle subtended at the ground observation point by the aircraft positions 10s apart is 30°, what is the speed of the aircraft?
Sol: The positions of the observer and the aircraft are depicted in the following figure.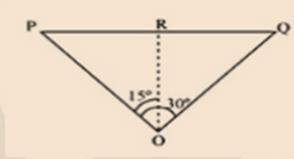
Height of the aircraft from ground is given as, OR = 3400m
Angle subtended between the positions is given as, ∠POQ = 30°
Time = 10s
In ΔPRO, we can write:
tan 15° = PR / OR
⇒ PR = OR tan 15°
⇒ PR = 3400 × tan 15°
ΔPRO is similar to ΔRQO.
PR = RQ
⇒ PQ = PR + RQ
⇒ PQ = 2PR = 2 × 3400 tan 15°
⇒ PQ = 6800 × 0.268 = 1822.4m
Therefore, speed of the aircraft
1822.4 / 10 = 182.24m/s
Q8. In a harbour, wind is blowing at the speed of 72km/h and the flag on the mast of a boat anchored in the harbour flutters along the N-E direction. If the boat starts moving at a speed of 51km/h to the north, what is the direction of the flag on the mast of the boat?
Sol: Wind speed =72 km/h towards N–E. Boat speed =51 km/h towards N.
Direction of the flag = direction of apparent wind on the boat: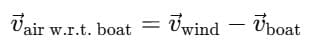
Resolve into East (i) and North (j):
The flag points almost due east, very slightly south of east (about 0.1°).
Q9. A fighter plane flying horizontally at an altitude of 1.5km with speed 720km/h passes directly overhead an anti-aircraft gun. At what minimum vertical altitude should the gun be fired for the shell to hit the plane? Take g = 10m/s2.
Sol: Height of the fighter plane is given as, h = 1.5km = 1500m
Speed of the fighter plane is given as, v = 720km/h = 200m/s
Let β be the angle with the vertical so that the shell hits the plane.
Muzzle velocity of the gun, u = 600m/s
Time taken by the shell to hit the plane = t
Horizontal distance travelled by the shell = ux t
Distance travelled by the plane = v t
Therefore, these two distances should be equal
ux t = v t
u sin β = v
⇒ 600 sin β = 200
⇒ sin β = 200 / 600 = 1 / 3
⇒ β = sin-1(1 / 3)
In order to avoid being hit by the shell, the pilot must fly the plane at an altitude (h) higher than the maximum height achieved by the shell.
H = (u2 sin2(90 - β)) / (2g)
= (u2 cos2β) / (2g)
= (6002 × cos2 (1 / 3)) / (2 × 10)
= 16006.42 m
= 16km, which is the required height.
Q10. The blades of an aeroplane propeller are rotating at the rate of 600 revolutions per minute. Calculate its angular velocity.
Sol: We can write, v = 600 rev/min
⇒ v = 600 / 60 rev/sec
ω = 2πv = 2π × 600 / 60
⇒ ω = 20π rad/sec, which is the required angular velocity.
|
96 videos|367 docs|98 tests
|
FAQs on Numerical Problems: Motion in a Plane - Physics Class 11 - NEET
| 1. What is the difference between scalar and vector quantities in motion? |  |
| 2. How do you calculate the resultant displacement when two vectors are involved? |  |
| 3. What are the equations of motion in two dimensions? |  |
| 4. How can projectile motion be described in terms of its components? |  |
| 5. What is the significance of the angle of projection in projectile motion? |  |
















