Class 6 Exam > Class 6 Notes > Mathematics Class 6 ICSE > Revision Notes: Fractions
Revision Notes: Fractions | Mathematics Class 6 ICSE PDF Download
A fraction is a part of whole and is written as (a/b), where ‘a’ and ‘b’ are integers and 𝐛 ≠ 𝟎
Ex: 2/3
- The upper term ‘a’ is called as “numerator” and lower term ‘b’ is called the “denominator”. Thus 𝑭𝒓𝒂𝒄𝒕𝒊𝒐𝒏 = (𝐍𝐮𝐦𝐞𝐫𝐚𝐭𝐨𝐫/𝐃𝐞𝐦𝐨𝐦𝐢𝐧𝐚𝐭𝐨𝐫)
- Value of fraction = 1, if numerator = denominator
- Value of fraction = 0, if numerator = 0; and denominator ≠ 0
- Value of fraction is not defined if denominator = 0
- Value of fraction remains unaltered if it is multiplied and divided by same number
Kinds of Fractions
- Simple Fraction: Fraction whose both terms integers.
Ex: 3/8, -7/3 - Complex Fraction: Fraction whose one or both terms are fractional numbers.
Ex: 5/(8÷2) ; (9÷3)/(8÷2) - Decimal Fraction: Faction with denominator 10, 100, 1000, 10000.....
Ex: 5/10, 56/100
Decimal Fraction = 3471/100 = 𝟑𝟒.𝟕𝟏 read as thirty four point seven one and 34 is the integral part and 0.71 is the decimal part. Adding or removing zeros at its extreme right will not change the value of fraction
Ex: 4.3 = 4.300; 3.6800 = 3.68 - Vulgar Fraction: Fraction whose denominators are not 10, 100, 1000...
Ex: 3/8, 4/2
Converting Decimal Fraction to Vulgar Fraction
Remove decimal point and write resulting number as numerator and in denominator add as many zeros to right of one (1) as decimal places in given number
Ex: 0.088 = 8/1000
Reduce to simplest form 8/1000 = 11/125 - Proper Fraction: Fraction whose numnerator is less than or positive than its denominator.
Ex: 5/12, 135/245 - Improper Fraction: Fraction whose numnerator is greater than its denominator.
Ex: 12/7, 335/245 - Mixed Fraction: Fraction expressed as combination of an integer and a proper fraction.
Improper fraction expressed as Mixed fraction.
- Ex: 49/12 can be written as 4(5/12) On dividing 49 by 12 we get 4 as quotient (Integer) as 5 as remainder (Numerator) and denominator is unaltered
Mixed fraction expressed as Improper fraction.
- Ex∶ 5(7/8) can be written as 47/8; Numerator = (5 × 8) + 7 = 40 + 7 = 47 and Denominator is unaltered.
Fractions
- Equivalent Fractions: Fractions having same value are called equivalent fractions.
Ex: 20/25 Dividing numnerator and denominator by 5 we get 4/5.
28/35 on dividing by 7 we get 4/5.
Hence 20/25 and 28/35 are equivalent fractions - Like Fractions: Fractions having same denominators are called like fractions.
Ex: 3/8, 5/4, 9/8 ...... - Unlike Fractions: Fractions with different denominators are called unlike fractions.
Ex: 2/6, 7/5, 9/3 ... - Bodmas: Bracket Of Division Multiplication Addition and Subtraction "of" between any two fractions is to be used as multiplication.
Converting Unlike to like fractions:
- Find LCM of denominators of all given fractions
- Multiply each fraction’s numerator and denominator with same number such that denominator is equal to the LCM
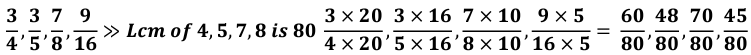
- Comparing Fractions: Convert the fractions into like fractions and then the fraction with the greater numerator is greater.
Inserting Fraction between given fraction:
- Add numerator of the given fractions to get the required numerator
- Similarly add denominator to get the required denominator

Fundamental Operations on Fractions
Multiplication
- Multiplication by an integer Keep denominator unchanged, multiply numerator by integer and simplify
Ex: 4 x (4/12) = 16/12 = 4/3 - Multiplication by fraction Multiply numerators together and denominators separately together and simplify
Ex:
Addition and Subtraction
- Fractions having same denominator 6(2/5) and 4(4/5)
Convert into improper fraction 32/5 ± 24/5
Add / Sub the numerators of each fraction and denominator is retained.
(32 ± 24)/5 If the resultant is improper fraction convert to Mixed fraction - Fractions having different denominator 6(2/5) and 4(4/4)
Convert into improper fraction 32/5 ± 20/4
Take L.C.M of numerators L.C.M (5, 4) = 20 which is the denominator Multiply each fraction with LCM resultant are added/subtracted to numerator (32/5 x 20) ± (20/4 x 20) = (32×4) ± (20×5) = 128 ± 100
Division
- Division in fraction Multiply fraction by the reciprocal of the divisor and simplify

- Division in decimal fraction Division by 10, 100,1000,…..shift decimal point to left as many digits as the number of zeros
Ex: 𝟒𝟑.𝟒 ÷ 𝟏𝟎𝟎 = 𝟎.𝟒𝟑𝟒 - Division of decimal fraction by an integer is done like ordinary division and the decimal point is placed to quotient such that its number of digits after decimal point is equal to digits after decimal point in the dividend
Ex: 𝟓.𝟔𝟒 ÷ 𝟐 = 𝟐.𝟖𝟐
The document Revision Notes: Fractions | Mathematics Class 6 ICSE is a part of the Class 6 Course Mathematics Class 6 ICSE.
All you need of Class 6 at this link: Class 6
|
44 videos|202 docs|24 tests
|
FAQs on Revision Notes: Fractions - Mathematics Class 6 ICSE
| 1. What are fractions and how are they represented? |  |
Ans. Fractions are numbers that represent a part of a whole. They are written in the form of \( \frac{a}{b} \), where \( a \) is the numerator (the number of parts we have) and \( b \) is the denominator (the total number of equal parts the whole is divided into). For example, in the fraction \( \frac{3}{4} \), 3 is the numerator and 4 is the denominator, meaning we have 3 out of 4 equal parts of a whole.
| 2. How do you add and subtract fractions? |  |
Ans. To add or subtract fractions, they must have a common denominator. If the denominators are the same, you simply add or subtract the numerators and keep the denominator the same. For example, to add \( \frac{1}{4} + \frac{2}{4} \), you add the numerators: \( 1 + 2 = 3 \), so the result is \( \frac{3}{4} \). If the fractions have different denominators, find a common denominator, convert the fractions, and then add or subtract the numerators.
| 3. What is the difference between proper fractions and improper fractions? |  |
Ans. Proper fractions are fractions where the numerator is less than the denominator, meaning the value is less than one (e.g., \( \frac{2}{5} \)). Improper fractions, on the other hand, have a numerator that is greater than or equal to the denominator, which means the value is one or more (e.g., \( \frac{5}{4} \)). Improper fractions can also be expressed as mixed numbers, which combine a whole number and a proper fraction (e.g., \( 1\frac{1}{4} \)).
| 4. How can you convert a mixed number to an improper fraction? |  |
Ans. To convert a mixed number to an improper fraction, multiply the whole number by the denominator of the fractional part and add the numerator. This sum becomes the new numerator, while the denominator remains the same. For example, to convert \( 2\frac{3}{5} \) to an improper fraction: \( 2 \times 5 + 3 = 10 + 3 = 13 \), so it becomes \( \frac{13}{5} \).
| 5. What are equivalent fractions and how do you find them? |  |
Ans. Equivalent fractions are different fractions that represent the same value or proportion of a whole. To find equivalent fractions, you can multiply or divide both the numerator and the denominator of a fraction by the same non-zero number. For example, \( \frac{1}{2} \) is equivalent to \( \frac{2}{4} \) because both fractions represent the same portion of a whole.
Related Searches




















