Numerical Problems: Electric Charges and Fields | Physics Class 12 - NEET PDF Download
Q1. An electric dipole of length 2 cm is placed with its axis making an angle of 30° to a uniform electric field 105 N/C. If it experiences a torque of 10√3 Nm, then potential energy of dipole will
Sol: τ = P E sin 30
10√3 = PE / 2
PE = 20√3
Potential Energy = –PE cos 30
Potential energy = –20√3 × √3 / 2
= –10 × 3 = –30 J
Q2. Calculate the net force acting on the charge present at the origin.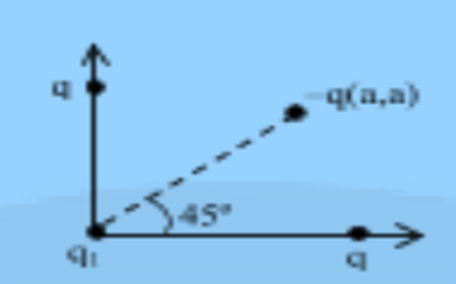
Sol: F'' = √2 F
F'' = k q q1 / a2
F' = k q q1 / (√2 a)2 = k q q1 / 2a2
∴ FNet = F'' – F'
= k q q1 / a2 (√2 – 1/2)
Q3. A hollow charged metal sphere has radius r. If the potential difference between its surface and a point at a distance 3r from the centre is V, then electric field intensity at distance 3r from the centre is
Sol: VA – VB = kQ / r – kQ / 3r
= kQ / 3r, V = 2 kQ / 3r
E = kQ / (3r)2 = kQ / 9r2 = 3 r V / 2 9r2. E = V / 6r
Q4. If two like charges of magnitude 1 × 10-9 coulomb and 9 × 10-9 coulomb are separated by a distance of 1 meter, then the point on the line joining the charges, where the force experienced by a charge placed at that point is zero, is
Sol: F21 = F23
or k q q1 / x2 = k q q2 / (1 - x)2
or 1 × 10-9 / x2 = 9 × 10-9 / (1 - x)2
or 1 / x2 = 9 / (1 - x)2
or 1 / x = 3 / (1 - x)
or 1 - x = 3x
or x = 0.25 m from 1 × 10-9C
∴ From 9 × 10-9C, distance
= 1 - x
= 1 - 0.25
= 0.75
Q5. A charge Q has to be divided between two solid spheres of radius 'R' which are at distance d from each other (d >> R). What should be the value of charge, which we should place on spheres, so that the force of attraction between them is maximum?
Sol: Let us place a quantum of charge 'q' on the first sphere, so we have charge Q-q on the other sphere. The force of attraction between the spheres is
F = (Q - q)q / 4πϵ0d2
dF/dq = 1 / 4πϵ0d2 [(Q - q) - q] = 0
∴ q = Q/2
Q6. The electric potential V at any point (x, y, z) in space is given by V = 6x2 volt, where all the distances are measured in metre. The electric field at the point (1 m, 0, 2 m) is
Sol: The potential V is a scalar function, whereas the field E is a vector function. The three components of E are given as
Ex = - ∂V / ∂x = - ∂ / ∂x (6x2) = -12x
Ey = - ∂V / ∂y = - ∂ / ∂y (6x2) = 0
Ez = - ∂V / ∂z = - ∂ / ∂z (6x2) = 0
∴ E = -12xî + 0ĵ + 0k̂ = -12xî
at the given point, x = 1,
∴ E = -12î
Q7. How many electrons should be removed from a coin of mass 1.6 gm, so that it may float in electric field intensity 105 N/C directed upwards?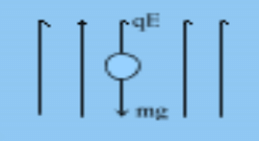
Sol: qE = mg
neE = mg
n = mg / eE = 1.6×10-3 × 9.8 / 1.6×10-19 × 105
n = 9.8 × 107
Q8. An electric dipole, made up of a positive and a negative charge, each of 1μC and placed at a distance 2 cm apart, is placed in an electric field 105 N/C. Compute the maximum torque which the field can exert on the dipole, and the work that must be done to turn the dipole from a position θ = 0° to θ = 180°.
Sol: The torque exerted by an electric field E on a dipole of moment p is given by
τ = pE sinθ,
where θ is the angle which the dipole is making with the field.
τ is a maximum, when θ = 90°. That is
∴ τmax = pE
Here p = q(2ℓ) = 1×10-6 × 0.02C/m and E = 105N/C
∴ τmax = 1×10-6 × 0.02 × 105 = 2×10-3N-m
The work done in rotating the dipole from an angle θ0 to θ is given by
W = ∫θ₀θ pE sinθ dθ = pE (cosθ0 - cosθ)
Here θ0 = 0° and θ = 180°
∴ W = pE (cos0° - cos180°) = 2pE = 4×10-3N-m or Joule
Q9. Potential in the x-y plane is given as V = 5(x2 + xy) volts. The electric field at the point (1, -2) will be
Sol: Ex = - ∂V / ∂x = - (10x + 5y) = -10 + 10 = 0
Ey = - ∂V / ∂y = -5x = -5
∴ E = -5ĵ V/m.
Q10. A long string with a charge of λ per unit length passes through an imaginary cube of edge a. The maximum flux of the electric field through the cube will be
Sol: The maximum length of the string which can fit into the cube is √3a, equal to its body diagonal. The total charge inside the cube is √3λa, and hence the total flux through the cube is √3λa / ε₀.
|
74 videos|314 docs|88 tests
|
FAQs on Numerical Problems: Electric Charges and Fields - Physics Class 12 - NEET
| 1. What is the difference between conductors and insulators in terms of electric charge? |  |
| 2. How do electric fields interact with charged particles? |  |
| 3. What is Coulomb's Law and how is it applied? |  |
| 4. What is the principle of superposition in electric fields? |  |
| 5. How can we calculate the electric field due to a point charge? |  |
















