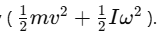Mnemonics: System of Particles and Rotational Motion | Physics Class 11 - NEET PDF Download
| Table of contents |

|
| 1. Moment of Inertia and Axis Theorems |

|
| 2. Rolling Motion |

|
| 3. Conservation of Angular Momentum |

|
| 4. Rolling Motion |

|
1. Moment of Inertia and Axis Theorems
Mnemonics:"Mom Prefers Perfect Rotation"Breakdown:
Mom – Moment of Inertia (I = Σmr²)
Prefers – Parallel Axis Theorem
Perfect – Perpendicular Axis Theorem
Rotation – Radius of Gyration
Moment of Inertia (I = Σmr²): Measures the rotational inertia of a body about an axis; depends on mass and the square of the distance from the axis.
Perpendicular Axis Theorem: For a planar body, Iz=Ix+Iy, where the axes lie perpendicular to each other.
Parallel Axis Theorem: I = ICOM+Md2, used to find moment of inertia about any axis parallel to one through the center of mass.
Radius of Gyration (K): The distance from the axis at which the total mass of the body can be imagined to be concentrated for the same moment of inertia I=MK2.
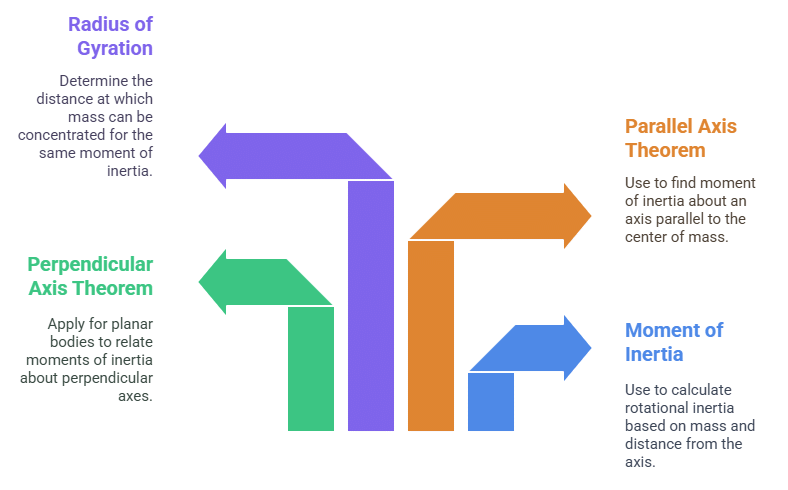
2. Rolling Motion
Mnemonic: "Real Wheels Roll Carefully"
- Real – Rolling without slipping
- Wheels – Work and Energy in rolling
- Roll– Rolling Condition (v = Rω)
- Carefully– Combined Translation + Rotation
Rolling without slipping: The bottom point of the rolling object is momentarily at rest with respect to the surface.
Work and Energy in rolling: Includes both translational and rotational kinetic energy
Rolling Condition: The linear velocity of the center of mass is related to angular velocity by v=Rω.
Combined Translation + Rotation: A rolling object moves forward (translation) while spinning (rotation) simultaneously.
3. Conservation of Angular Momentum
Mnemonic: "Angular Momentum Never Dies"
A – Angular momentum (L = Iω)
M – Moment of inertia (I)
N – No external torque
D – Decrease in moment of inertia increases angular velocity
Angular Momentum (L = Iω): Product of moment of inertia and angular velocity.
Moment of Inertia (I): Depends on mass distribution relative to the axis.
No External Torque: If no external torque acts, angular momentum remains conserved.
Decrease in I ⇒ Increase in ω: When a system (like a spinning skater) reduces its moment of inertia (pulls arms in), angular velocity increases to conserve L.

4. Rolling Motion
Mnemonic: "Round Bicycles Drive Smoothly"
Round – Rolling Motion
Bicycles – Both Rotational and Translational motion
Drive – Displacement is combination of rotation and translation
Smoothly – Slip is absent (Rolling without slipping)
Rolling Motion occurs when an object moves forward while rotating.
Both rotational and translational energies are involved in the motion.
Displacement is due to both the rotation of the object and its forward movement.
Smooth, slip-free rolling happens when v=Rω, i.e., the velocity at the point of contact is zero.
|
95 videos|367 docs|98 tests
|
FAQs on Mnemonics: System of Particles and Rotational Motion - Physics Class 11 - NEET
| 1. What is the definition of the center of mass in a system of particles? |  |
| 2. How is linear momentum defined for a system of particles? |  |
| 3. What are the components of torque, and how are they calculated? |  |
| 4. What factors influence the moment of inertia of an object? |  |
| 5. How is rotational kinetic energy calculated for a rotating object? |  |