Class 6 Exam > Class 6 Notes > Maths Olympiad Class 6 > Revision Notes: Symmetry - Including Constructions
Revision Notes: Symmetry - Including Constructions | Maths Olympiad Class 6 PDF Download
Linear Symmetry
Symmetry
A plane figure is said to have symmetry (or linear symmetry) if on folding the figure about a line on it, the two parts of figures exactly coincide.
The line about which the figure is symmetrical is called "line of symmetry" or "an axis of symmetry" or simply a "mirror line"
Line segments shows the line of symmetry for given polygons
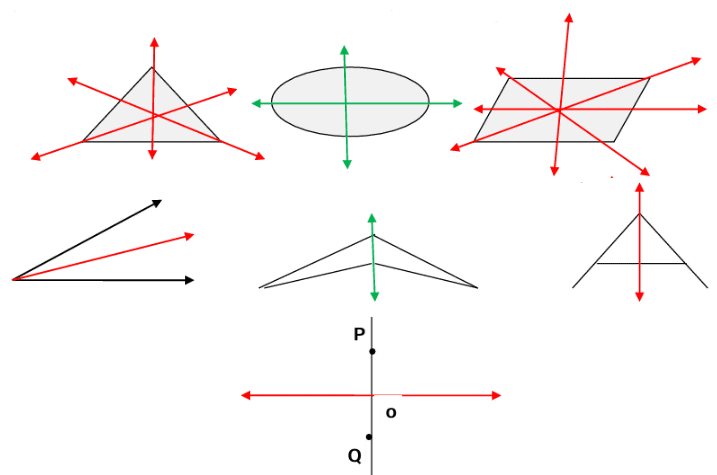
Symmetric point: In the figure above point P on the line, when folded along the line of syymetry co insides with Q. Hence Q is said to be "symmetric point".
To locate symmetric point of point P:
(i) Draw a perpendicular line OP from point P to the line of symmetry
(ii) Extend PO and cut OQ = OP
The document Revision Notes: Symmetry - Including Constructions | Maths Olympiad Class 6 is a part of the Class 6 Course Maths Olympiad Class 6.
All you need of Class 6 at this link: Class 6
|
30 videos|115 docs|59 tests
|
FAQs on Revision Notes: Symmetry - Including Constructions - Maths Olympiad Class 6
| 1. What is linear symmetry in geometry? |  |
Ans.Linear symmetry, also known as reflection symmetry, occurs when a shape can be divided into two identical halves that are mirror images of each other. If you draw a line through the shape (the line of symmetry), both sides will look the same.
| 2. How can I identify lines of symmetry in different shapes? | |
Ans.To identify lines of symmetry, you can fold the shape along different lines. If the two halves match perfectly when folded, that line is a line of symmetry. For example, a square has four lines of symmetry, while a circle has infinite lines of symmetry.
| 3. Can you explain the process of constructing symmetrical shapes? | |
Ans.To construct symmetrical shapes, start by drawing the line of symmetry. Then, use a ruler or compass to measure equal distances from the line to create points on both sides. Connect these points to form the shape, ensuring both halves are identical.
| 4. What are some examples of linear symmetry in everyday life? | |
Ans.Examples of linear symmetry in everyday life include butterfly wings, human faces, and many logos. Nature often displays symmetry, such as in flowers and leaves, where one side mirrors the other.
| 5. Why is understanding symmetry important in mathematics and art? | |
Ans.Understanding symmetry is crucial in mathematics for solving problems related to shapes and patterns. In art, symmetry contributes to aesthetics, balance, and harmony in designs, making artworks visually appealing and organized.
About this Document
Sep 24, 2025
Last updated
Related Exams
Document Description: Revision Notes: Symmetry - Including Constructions for Class 6 2025 is part of Maths Olympiad Class 6 preparation.
The notes and questions for Revision Notes: Symmetry - Including Constructions have been prepared according to the Class 6 exam syllabus. Information about Revision Notes: Symmetry - Including Constructions covers topics
like Linear Symmetry and Revision Notes: Symmetry - Including Constructions Example, for Class 6 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Revision Notes: Symmetry - Including Constructions.
Introduction of Revision Notes: Symmetry - Including Constructions in English is available as part of our Maths Olympiad Class 6
for Class 6 & Revision Notes: Symmetry - Including Constructions in Hindi for Maths Olympiad Class 6 course.
Download more important topics related with notes, lectures and mock test series for Class 6
Exam by signing up for free. Class 6: Revision Notes: Symmetry - Including Constructions | Maths Olympiad Class 6
Description
Full syllabus notes, lecture & questions for Revision Notes: Symmetry - Including Constructions | Maths Olympiad Class 6 - Class 6 | Plus excerises question with solution to help you revise complete syllabus for Maths Olympiad Class 6 | Best notes, free PDF download
Information about Revision Notes: Symmetry - Including Constructions
In this doc you can find the meaning of Revision Notes: Symmetry - Including Constructions defined & explained in the simplest way possible. Besides explaining types of
Revision Notes: Symmetry - Including Constructions theory, EduRev gives you an ample number of questions to practice Revision Notes: Symmetry - Including Constructions tests, examples and also practice Class 6
tests
Related Searches
mock tests for examination
,Free
,practice quizzes
,Revision Notes: Symmetry - Including Constructions | Maths Olympiad Class 6
,Important questions
,MCQs
,study material
,Previous Year Questions with Solutions
,past year papers
,Summary
,Revision Notes: Symmetry - Including Constructions | Maths Olympiad Class 6
,Revision Notes: Symmetry - Including Constructions | Maths Olympiad Class 6
,Objective type Questions
,Semester Notes
,Sample Paper
,video lectures
,shortcuts and tricks
,Exam
,Extra Questions
,Viva Questions
,ppt
;
Additional Information about Revision Notes: Symmetry - Including Constructions for Class 6 Preparation
Revision Notes: Symmetry - Including Constructions Free PDF Download
The Revision Notes: Symmetry - Including Constructions is an invaluable resource that delves deep into the core of the Class 6 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Revision Notes: Symmetry - Including Constructions now and kickstart your journey towards success in the Class 6 exam.
Importance of Revision Notes: Symmetry - Including Constructions
The importance of Revision Notes: Symmetry - Including Constructions cannot be overstated, especially for Class 6 aspirants.
This document holds the key to success in the Class 6 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Revision Notes: Symmetry - Including Constructions
Revision Notes: Symmetry - Including Constructions Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Revision Notes: Symmetry - Including Constructions.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Revision Notes: Symmetry - Including Constructions Notes on EduRev are your ultimate resource for success.
Revision Notes: Symmetry - Including Constructions Class 6 Questions
The "Revision Notes: Symmetry - Including Constructions Class 6 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 6 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Revision Notes: Symmetry - Including Constructions on the App
Students of Class 6 can study Revision Notes: Symmetry - Including Constructions alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Revision Notes: Symmetry - Including Constructions,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Revision Notes: Symmetry - Including Constructions is prepared as per the latest Class 6 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup