Class 9 Exam > Class 9 Notes > Mathematics Class 9 ICSE > Revision Notes: Rational and Irrational Numbers
Revision Notes: Rational and Irrational Numbers | Mathematics Class 9 ICSE PDF Download
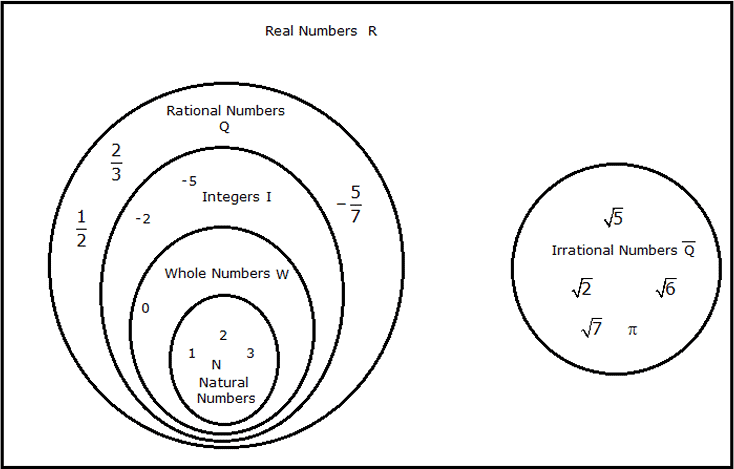
Rational Numbers
- A rational number is a number that can be expressed in the form a/b where
- a and b are integers, and b ≠ 0. The set of rational number is denoted by Q. Thus
Q = {a/b = a, b ∈ Z, b ≠ 0} - Between two rational numbers, there always exists infinite rational numbers.
- Every integer (positive, negative or Zero) and every decimal number is a rational number.
- All terminating and non-terminating but repeating (or periodic or recurring) decimals are rational numbers.
- Let x = p/q be a rational number, such that the prime factorisation of q is of the form 2n5m, where n, m are non-negative integers. Then, x has a decimal expansion which terminates.
- Every rational number can be expressed either as a terminating decimal or as a recurring decimal.
Irrational Numbers
- The real numbers, which are not rational, are called irrational numbers.
- The square roots, cube roots etc. of natural numbers are irrational numbers; if their exact value can not be obtained.
- All non-terminating non-repeating decimals are irrational numbers.
- π is an irrational number.
- If m is not a perfect square, the √m is irrational.
- If a and b are two positive numbers such that ab is not a perfect square, then
(a) A rational number between a and b is (a+b)/2
(b) An irrational number between a and b is √ab
More about Irrational Numbers
- For any two positive rational numbers x and y,
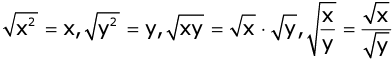
If √x and √y are irrational numbers, then,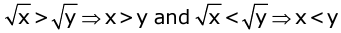
If √x and √y are irrational numbers, then,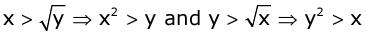
- If a + b√x = c + d√x ⇒ a = c and b = d
- The negative of an irrational number is always irrational.
- The sum of a rational and an irrational number is always irrational.
- The product of a non-zero rational number and an irrational number is always irrational.
- The sum, difference, product and quotient of two irrational numbers may not be an irrational number.
Real Numbers
- The set of the union of rational and irrational numbers forms a set of real numbers. Thus a real number can be associated with a point on the number line.
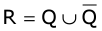
Surds
- If x is a positive rational number and n is a positive integer such that
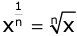 is irrational, then x1/n is called a surd or a radical.
is irrational, then x1/n is called a surd or a radical. - Every surd is an irrational number, but every irrational number is not a surd. π is an irrational number but it is not a surd.
- When two irrational numbers are multiplied, their product is called a rational number. This process of removing the radical sign from the denominator is called rationalization and the two irrational numbers are called rationalizing factors of each other.
- The irrational numbers
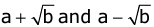 are called conjugates of each other.
are called conjugates of each other. - A number of the form
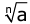 is called a surd of the order n where a is a positive rational number which is not equal to the nth power of a rational number and n is a natural number greater than or equal to 2.
is called a surd of the order n where a is a positive rational number which is not equal to the nth power of a rational number and n is a natural number greater than or equal to 2.
The document Revision Notes: Rational and Irrational Numbers | Mathematics Class 9 ICSE is a part of the Class 9 Course Mathematics Class 9 ICSE.
All you need of Class 9 at this link: Class 9
|
64 videos|136 docs|28 tests
|
FAQs on Revision Notes: Rational and Irrational Numbers - Mathematics Class 9 ICSE
| 1. What are rational numbers? |  |
Ans. Rational numbers are numbers that can be expressed in the form of a fraction $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$. Examples of rational numbers include 1/2, -3, and 4.75, as they can all be represented as fractions or whole numbers.
| 2. What are irrational numbers? |  |
Ans. Irrational numbers are numbers that cannot be expressed as a simple fraction. They have non-repeating, non-terminating decimal expansions. Common examples of irrational numbers include $\sqrt{2}$, $\pi$, and $e$. These numbers cannot be exactly represented as a fraction of two integers.
| 3. How can you identify whether a number is rational or irrational? |  |
Ans. To identify if a number is rational or irrational, check if it can be written as a fraction of two integers. If it can, it is rational. If it has a decimal form that neither terminates nor repeats, such as 0.101001001..., it is irrational. For example, the number 3.14 is rational (as it can be expressed as $\frac{314}{100}$), while the number $\sqrt{3}$ is irrational.
| 4. Can a rational number be a whole number? |  |
Ans. Yes, a rational number can be a whole number. Whole numbers like 0, 1, 2, and 3 can be expressed as fractions (for example, 2 can be written as $\frac{2}{1}$). Therefore, all whole numbers are also rational numbers because they meet the criteria of being expressed in the form $\frac{p}{q}$.
| 5. What is the difference between rational and irrational numbers in terms of their decimal representation? |  |
Ans. The difference in decimal representation between rational and irrational numbers is significant. Rational numbers have decimal representations that are either terminating (like 0.75) or repeating (like 0.333...). In contrast, irrational numbers have decimal expansions that are non-terminating and non-repeating (like 0.14159265...). This distinction helps in classifying numbers into these two categories.
Related Searches
















