Class 9 Exam > Class 9 Notes > Mathematics Class 9 ICSE > Revision Notes: Simultaneous (Linear) Equations
Revision Notes: Simultaneous (Linear) Equations | Mathematics Class 9 ICSE PDF Download
Important concepts
- An equation is a statement which relates two expressions with an equality sign.
- The equation in which the variable is of the first order is called a simple or a linear equation.
- An equation remains unaffected:
(i) if we add the same quantity to both sides.
(ii) if we subtract the same quantity from both sides.
(iii) if we multiply both sides by the same quantity.
(iv) if we divide both sides by a same non zero quantity. - To solve a problem based on equations, first translate the relation given in the problem into an algebraic equation and then solve the equation.
- Steps in solving a linear equation:
(i) Simplify all brackets, fractions, etc., if required.
(ii) Bring all the terms containing the variables on one side and all the constant terms on the other side.
(iii) Solve the equation, obtained in the previous step, to get the value of its variable. - Consecutive integers, natural numbers and whole numbers are taken as, n, n+1, n+2, n+3,….
- Consecutive even integers, natural numbers and whole numbers differ by 2 and hence are taken as, n, n+2, n+4, n+6,….
- Consecutive odd integers, natural numbers and whole numbers differ by 2 and hence are taken as, n, n+2, n+4, n+6, ....
Related Terms
- If two linear equations in the same two variables x, y are satisfied by the same pair of values of x and y then such linear equations are called simultaneous linear equations.
Methods to Solve Simultaneous Linear Equations
- Elimination Method: In this method, we eliminate either of the unknown quantity by addition or subtraction of the equation. Then we get an equation in one variable only which can be easily solved.
- Substitution Method: In this method, first, we solve one equation for one unknown in terms of the other unknown. Then we substitute the expression for this unknown in the second equation. After solving the resulting equation, we obtain the value of one unknown; substitute this value in one of the given equations to find the value of second unknown.
The following example depicts the method of elimination as well as substitution.
Example:
Solve: x + y = 7;5x + 2y = 7
Solution: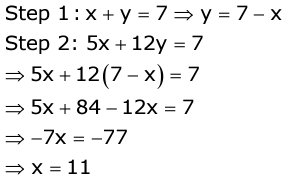
Step 3:
y = 7 - x ⇒ y = 7 - 11 = -4
∴ Solution is: x = 11 and y = -4 - Method of elimination by equating coefficients
Step 1: Multiply one or both of the equations by a suitable number or numbers such that the coefficients of x or the coefficients of y in both the equations become numerically equal.
Step 2: Add or subtract one equation from the other
Step 3: Solve the resulting equation
Step 4: Substitute this value in any of the two equations and find the value of the other unknown.
Ex: Solve: 7x + 6y = 61;5x - 8y = - 23
Sol.: 7x + 6y = 71 ...(1)
5x - 8y = -23 ...(2)
Step 1: Multiply equation (1) by 8 and equation (2) by 6.
The resulting equations are:
56x + 48y = 568 ...(3)
30x - 48y = 138 ...(4)
Step 2:
Adding equations (3) and (4):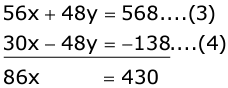
Step 3:
86x = 430
⇒ x = 430/86 = 5
Step 4:
Substituting x=5 in equation (1), we have
7 x (5) + 6y = 71
⇒ 35 + 6y = 71
⇒ 6y = 71 - 35
⇒ 6y = 36
⇒ y = 6
Hence x = 5 and y = 6
Problems Based On Simultaneous Equations
- To Solve a problem based on simultaneous equations:
Step 1: Assume the two variables as x and y
Step 2: Form two equations in x and y
Step 3: Solve the equations using any method
Graphical Solution
Graphs of Linear Equations in Two Variables Related Terms
- An equation of the form ax + by + c = 0 is called a linear equation in two variables.
- In the equation, ax + by + c = 0 ; x and y are the variables and a, b and c are the constants.
To Draw a Graph of a Linear Equation
- Make x or y, the subject of the equation.
- Give at least three suitable values to the variable on the right-hand side and find the corresponding values of the variable on the left hand side.
- Construct a table for the different pairs of values of x and y.
- Plot at least three ordered pairs (points) from the table on a graph paper.
- Draw a straight line passing through the points plotted on the graph.
Example: Draw the graph of 3x + 2y = 6:
Step 1: 3x + 2y = 6
⇒ 2y = 6 - 3x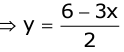 [Making y, the subject]
[Making y, the subject]
Step 2: Now give at least three different values to the variable x and find the corresponding values of y.
Let x = 0; then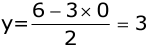
Let x = 2; then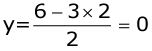
Let x = 4; then
Step 3: Therefore, table for x and y is: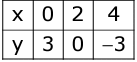
Step 4: Plot the points (0, 3) , (2, 0) and (4, -3) on a graph paper.
Draw a straight line passing through the points plotted on the graph paper.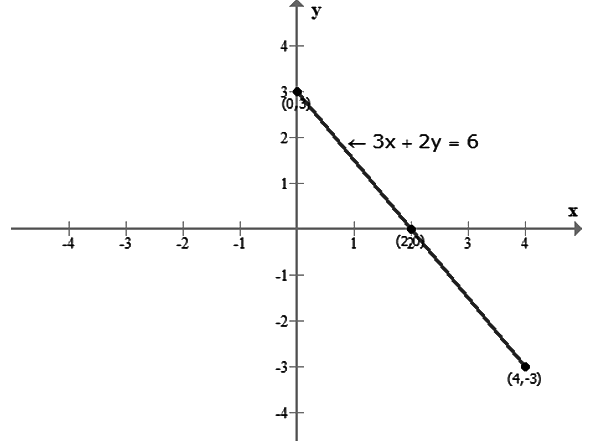
Graphs of Coordinate Axes
- The equation of x-axis is y = 0.
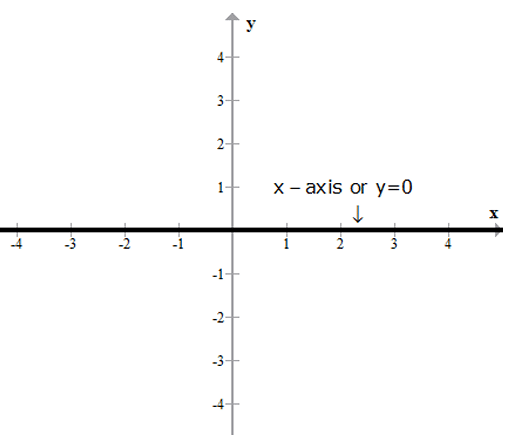
- The equation of y-axis is x = 0
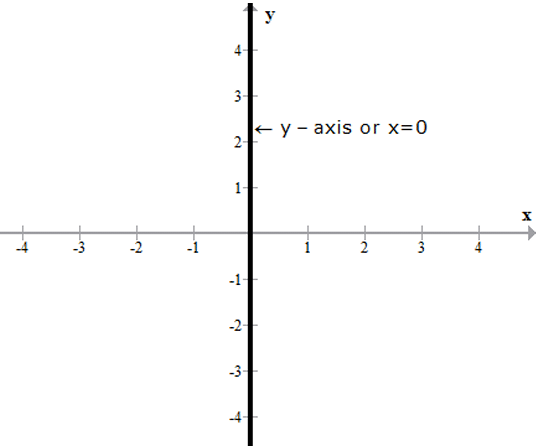
Graphs of Some Special Functions
- The graph of x = a (a is some constant) is a straight line parallel to y-axis and at a distance of ‘a’ units from the y-axis
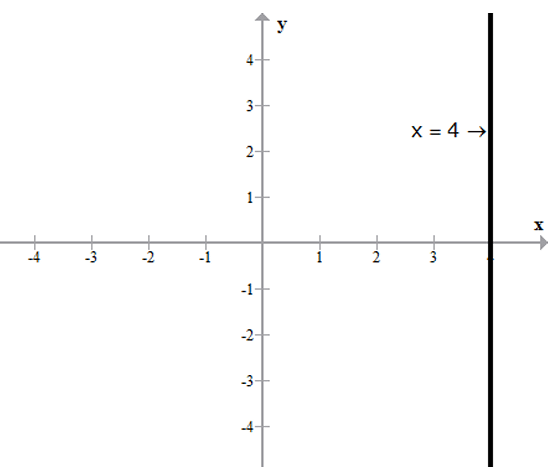
- The graph of y = b (b is some constant) is a straight line parallel to x-axis and at a distance of ‘b’ units from the x-axis
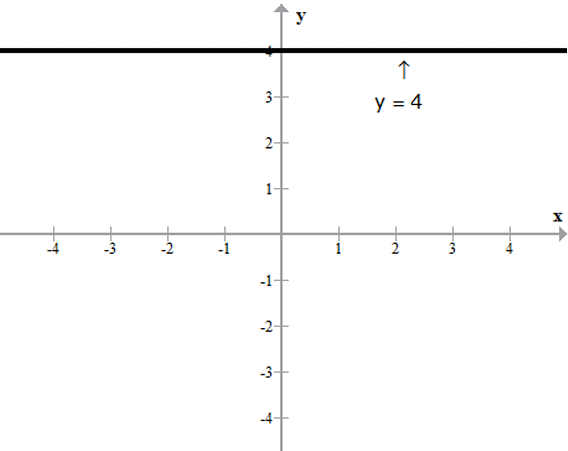
Graphical Solution of Simultaneous Linear Equations
- In order to solve simultaneous linear equations graphically:
Step 1: Draw a graph for each given equations
Step 2: Find the coordinates of the point of intersection of the two lines drawn.
Step 3: The coordinates of the point of intersection gives the solution of the given equation.
Example: Solve the following system of equations graphically: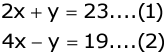
Now consider equation (1).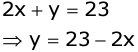
Thus the table for equation (1) is: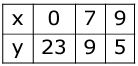
Plot the points (0, 23) , (7, 9) and (9, 5) on a graph paper.
Let us consider equation (2).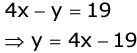
Thus the table for equation (1) is:
Plot the points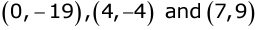
on the same graph paper.
Thus, we have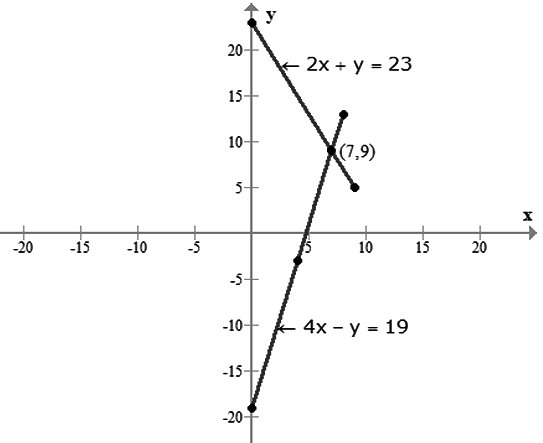 It is clear from the graph that the point of intersection of the given system of equations is (7, 9).
It is clear from the graph that the point of intersection of the given system of equations is (7, 9).
The document Revision Notes: Simultaneous (Linear) Equations | Mathematics Class 9 ICSE is a part of the Class 9 Course Mathematics Class 9 ICSE.
All you need of Class 9 at this link: Class 9
|
28 videos|171 docs|28 tests
|
FAQs on Revision Notes: Simultaneous (Linear) Equations - Mathematics Class 9 ICSE
| 1. What are simultaneous linear equations? |  |
Ans. Simultaneous linear equations are a set of equations with multiple variables that are solved together, as they share common solutions. For example, two equations like \(2x + 3y = 6\) and \(x - y = 1\) are simultaneous equations. The solution is a pair of values (x, y) that satisfy both equations at the same time.
| 2. How can graphical methods be used to solve simultaneous equations? |  |
Ans. Graphical methods involve plotting both equations on a graph. The point where the two lines intersect represents the solution to the simultaneous equations. For instance, if one line represents \(y = 2x + 1\) and the other \(y = -x + 4\), the intersection point of these lines gives the values of x and y that solve both equations.
| 3. What are the steps to graphically solve simultaneous equations? |  |
Ans. The steps to graphically solve simultaneous equations include:
1. Rearranging both equations in the form \(y = mx + c\) (slope-intercept form).
2. Plotting the lines on a graph using at least two points for each equation.
3. Identifying the point of intersection of the two lines.
4. Reading the coordinates of the intersection point, which gives the solution to the equations.
| 4. What is the significance of the point of intersection in graphical solutions? |  |
Ans. The point of intersection in graphical solutions indicates the values of the variables that satisfy both equations simultaneously. If the lines intersect at a single point, it means there is a unique solution. If the lines are parallel, there is no solution, and if they coincide, there are infinitely many solutions.
| 5. Can graphical solutions be used for more than two equations? |  |
Ans. Graphical solutions are generally used for two equations because they can be represented on a two-dimensional graph. For three or more equations, a three-dimensional graph is required, which can be more complex. In such cases, other algebraic methods like substitution or elimination are usually preferred for finding solutions.
Related Searches





















