Class 9 Exam > Class 9 Notes > Mathematics Class 9 ICSE > Revision Notes: Indices
Revision Notes: Indices | Mathematics Class 9 ICSE PDF Download
Related terms
- A Power is the product of a number by itself. It is represented with a base number and an exponent.
We know that a3 = a x a x a
a7 = a x a x a .... 7 times
Similarly, am = a x a x a ... m times
In this example m is called index or exponent or power and a is called the base. - Index is a number which indicates how many times another number, the base, is being used as a repeated factor.
Laws of Indices
- am ÷ an = am + n (Product Law)
- am ÷ an =am – n (Quotient Law)
- (am)n = amn (Power Law)
- (a x b)m = am x bm
- a–m = 1/(am)
- If a ≠ 0 and n is a positive integer, then
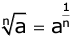
- If a ≠ 0 and n is a positive integer, then
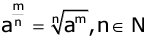
- For any non-zero, a,
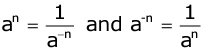
- For any non-zero number raised to the power zero is always equal to unity,
That is, a0 =1 - (-a)m = am; if m is an even number
- (-a)m = -am; if m is an odd number
The document Revision Notes: Indices | Mathematics Class 9 ICSE is a part of the Class 9 Course Mathematics Class 9 ICSE.
All you need of Class 9 at this link: Class 9
|
64 videos|136 docs|28 tests
|
FAQs on Revision Notes: Indices - Mathematics Class 9 ICSE
| 1. What are indices in mathematics and why are they important? |  |
Ans. Indices, also known as exponents or powers, are a way to express repeated multiplication of a number by itself. For example, \( a^n \) means \( a \) multiplied by itself \( n \) times. They are important because they simplify mathematical expressions, making calculations easier and more efficient, especially in algebra and higher-level mathematics.
| 2. How do you simplify expressions with indices? | |
Ans. To simplify expressions with indices, you can use the laws of indices, which include:
1. \( a^m \times a^n = a^{m+n} \)
2. \( \frac{a^m}{a^n} = a^{m-n} \)
3. \( (a^m)^n = a^{m \times n} \)
4. \( a^0 = 1 \) (where \( a \neq 0 \))
By applying these laws, you can reduce complex expressions into simpler forms.
| 3. What is the difference between positive and negative indices? | |
Ans. Positive indices indicate how many times to multiply the base by itself, while negative indices represent the reciprocal of the base raised to the corresponding positive index. For example, \( a^{-n} = \frac{1}{a^n} \). This distinction is crucial for correctly manipulating expressions involving negative indices.
| 4. Can you provide examples of real-life applications of indices? | |
Ans. Indices are used in various real-life applications, such as calculating compound interest in finance, determining population growth in biology, and analyzing exponential decay in physics. They help model situations where quantities grow or shrink exponentially, making them essential in many fields.
| 5. What are some common mistakes students make when working with indices? | |
Ans. Common mistakes include forgetting the laws of indices, especially when adding or subtracting exponents, misapplying negative indices, and not simplifying expressions fully. It's important for students to practice and review the laws of indices to avoid these errors in calculations.
About this Document
4.63/5
Rating
Sep 30, 2025
Last updated
Document Description: Revision Notes: Indices for Class 9 2025 is part of Mathematics Class 9 ICSE preparation.
The notes and questions for Revision Notes: Indices have been prepared according to the Class 9 exam syllabus. Information about Revision Notes: Indices covers topics
like and Revision Notes: Indices Example, for Class 9 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Revision Notes: Indices.
Introduction of Revision Notes: Indices in English is available as part of our Mathematics Class 9 ICSE
for Class 9 & Revision Notes: Indices in Hindi for Mathematics Class 9 ICSE course.
Download more important topics related with notes, lectures and mock test series for Class 9
Exam by signing up for free. Class 9: Revision Notes: Indices | Mathematics Class 9 ICSE
Description
Full syllabus notes, lecture & questions for Revision Notes: Indices | Mathematics Class 9 ICSE - Class 9 | Plus excerises question with solution to help you revise complete syllabus for Mathematics Class 9 ICSE | Best notes, free PDF download
Information about Revision Notes: Indices
In this doc you can find the meaning of Revision Notes: Indices defined & explained in the simplest way possible. Besides explaining types of
Revision Notes: Indices theory, EduRev gives you an ample number of questions to practice Revision Notes: Indices tests, examples and also practice Class 9
tests
Related Searches
Objective type Questions
,Important questions
,video lectures
,Sample Paper
,mock tests for examination
,Previous Year Questions with Solutions
,Semester Notes
,past year papers
,study material
,Summary
,shortcuts and tricks
,Free
,ppt
,Viva Questions
,practice quizzes
,Revision Notes: Indices | Mathematics Class 9 ICSE
,Exam
,Extra Questions
,Revision Notes: Indices | Mathematics Class 9 ICSE
,Revision Notes: Indices | Mathematics Class 9 ICSE
,MCQs
;
Additional Information about Revision Notes: Indices for Class 9 Preparation
Revision Notes: Indices Free PDF Download
The Revision Notes: Indices is an invaluable resource that delves deep into the core of the Class 9 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Revision Notes: Indices now and kickstart your journey towards success in the Class 9 exam.
Importance of Revision Notes: Indices
The importance of Revision Notes: Indices cannot be overstated, especially for Class 9 aspirants.
This document holds the key to success in the Class 9 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Revision Notes: Indices
Revision Notes: Indices Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Revision Notes: Indices.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Revision Notes: Indices Notes on EduRev are your ultimate resource for success.
Revision Notes: Indices Class 9 Questions
The "Revision Notes: Indices Class 9 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 9 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Revision Notes: Indices on the App
Students of Class 9 can study Revision Notes: Indices alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Revision Notes: Indices,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Revision Notes: Indices is prepared as per the latest Class 9 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup