Class 9 Exam > Class 9 Notes > Mathematics Class 9 ICSE > Revision Notes: Distance Formula
Revision Notes: Distance Formula | Mathematics Class 9 ICSE PDF Download
- The distance between P(x1, y1) and Q(x2, y2) is
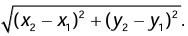
This is known as the distance formula. - The distance of a point P(x, y) from origin is
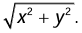
- The points A, B and C are collinear if AB + BC = AC.
- Three points A, B and C are the vertices of an equilateral triangle if AB = BC = CA.
- The points A, B and C are the vertices of an isosceles triangle if AB = BC or BC = CA or CA = AB.
- Three points A, B and C are the vertices of a right triangle if sum of squares of any two sides is equal to the square of the third side.
- For the given four points A, B, C and D:
(i) AB = BC = CD = DA; AC = BD ⇒ ABCD is a square.
(ii) AB = BC = CD = DA; AC ≠ BD ⇒ ABCD is a rhombus.
(iii) AB = CD, BC = DA; AC = BD ⇒ ABCD is a rectangle.
(iv) AB = CD, BC = DA; AC ≠ BD ⇒ ABCD is a parallelogram. - Circumcentre is the point of intersection of the perpendicular bisectors of the sides of the triangle.
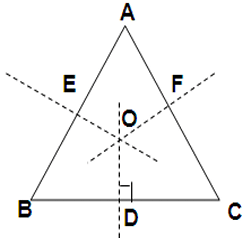O is the circumcentre of the triangle ABC.
The document Revision Notes: Distance Formula | Mathematics Class 9 ICSE is a part of the Class 9 Course Mathematics Class 9 ICSE.
All you need of Class 9 at this link: Class 9
|
28 videos|171 docs|28 tests
|
FAQs on Revision Notes: Distance Formula - Mathematics Class 9 ICSE
| 1. What is the distance formula in coordinate geometry? |  |
Ans. The distance formula is used to determine the distance between two points in a coordinate plane. If you have two points, A(x₁, y₁) and B(x₂, y₂), the distance (d) between them can be calculated using the formula:
\[ d = \sqrt{(x₂ - x₁)² + (y₂ - y₁)²} \]
| 2. How can the distance formula be derived using the Pythagorean theorem? | |
Ans. The distance formula can be derived from the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse (d) is equal to the sum of the squares of the other two sides. When finding the distance between two points (x₁, y₁) and (x₂, y₂), the horizontal distance is (x₂ - x₁) and the vertical distance is (y₂ - y₁). Therefore, applying the theorem gives:
\[ d² = (x₂ - x₁)² + (y₂ - y₁)² \]
Taking the square root of both sides leads to the distance formula.
| 3. Can the distance formula be used in three-dimensional space? | |
Ans. Yes, the distance formula can be extended to three-dimensional space. For two points A(x₁, y₁, z₁) and B(x₂, y₂, z₂), the distance (d) is calculated using the formula:
\[ d = \sqrt{(x₂ - x₁)² + (y₂ - y₁)² + (z₂ - z₁)²} \]
| 4. How do you find the distance between points with negative coordinates using the distance formula? | |
Ans. The distance formula works the same way regardless of whether the coordinates are positive or negative. Simply plug the coordinates into the formula. For example, for points A(-3, -4) and B(1, 2), the distance is calculated as follows:
\[ d = \sqrt{(1 - (-3))² + (2 - (-4))²} = \sqrt{(1 + 3)² + (2 + 4)²} = \sqrt{4² + 6²} = \sqrt{16 + 36} = \sqrt{52} = 2\sqrt{13} \]
| 5. What are some practical applications of the distance formula in real life? | |
Ans. The distance formula has various practical applications, such as in navigation systems for calculating distances between locations, in computer graphics for measuring distances between points in a digital image, and in physics for determining the displacement between two objects in motion. It is also used in fields such as architecture and engineering to calculate distances when designing structures.
About this Document
Sep 07, 2025
Last updated
Related Exams
Document Description: Revision Notes: Distance Formula for Class 9 2025 is part of Mathematics Class 9 ICSE preparation.
The notes and questions for Revision Notes: Distance Formula have been prepared according to the Class 9 exam syllabus. Information about Revision Notes: Distance Formula covers topics
like and Revision Notes: Distance Formula Example, for Class 9 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Revision Notes: Distance Formula.
Introduction of Revision Notes: Distance Formula in English is available as part of our Mathematics Class 9 ICSE
for Class 9 & Revision Notes: Distance Formula in Hindi for Mathematics Class 9 ICSE course.
Download more important topics related with notes, lectures and mock test series for Class 9
Exam by signing up for free. Class 9: Revision Notes: Distance Formula | Mathematics Class 9 ICSE
Description
Full syllabus notes, lecture & questions for Revision Notes: Distance Formula | Mathematics Class 9 ICSE - Class 9 | Plus excerises question with solution to help you revise complete syllabus for Mathematics Class 9 ICSE | Best notes, free PDF download
Information about Revision Notes: Distance Formula
In this doc you can find the meaning of Revision Notes: Distance Formula defined & explained in the simplest way possible. Besides explaining types of
Revision Notes: Distance Formula theory, EduRev gives you an ample number of questions to practice Revision Notes: Distance Formula tests, examples and also practice Class 9
tests
Related Searches
practice quizzes
,Summary
,Extra Questions
,video lectures
,ppt
,Revision Notes: Distance Formula | Mathematics Class 9 ICSE
,Exam
,MCQs
,Objective type Questions
,Sample Paper
,Free
,Previous Year Questions with Solutions
,study material
,Semester Notes
,Viva Questions
,Important questions
,mock tests for examination
,shortcuts and tricks
,Revision Notes: Distance Formula | Mathematics Class 9 ICSE
,Revision Notes: Distance Formula | Mathematics Class 9 ICSE
,past year papers
;
Additional Information about Revision Notes: Distance Formula for Class 9 Preparation
Revision Notes: Distance Formula Free PDF Download
The Revision Notes: Distance Formula is an invaluable resource that delves deep into the core of the Class 9 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Revision Notes: Distance Formula now and kickstart your journey towards success in the Class 9 exam.
Importance of Revision Notes: Distance Formula
The importance of Revision Notes: Distance Formula cannot be overstated, especially for Class 9 aspirants.
This document holds the key to success in the Class 9 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Revision Notes: Distance Formula
Revision Notes: Distance Formula Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Revision Notes: Distance Formula.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Revision Notes: Distance Formula Notes on EduRev are your ultimate resource for success.
Revision Notes: Distance Formula Class 9 Questions
The "Revision Notes: Distance Formula Class 9 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 9 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Revision Notes: Distance Formula on the App
Students of Class 9 can study Revision Notes: Distance Formula alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Revision Notes: Distance Formula,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Revision Notes: Distance Formula is prepared as per the latest Class 9 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup