Identifying Naked Pairs | Master Sudoku: From Beginner to Expert - Class 1 PDF Download
Naked Pairs
A Naked Pair is merely a Sudoku solving technique — and a very helpful one at that.
The phrase refers to pencil marks : specifically, when two cells in the same house have the exact same two pencil marks.
A ‘house' refers to a row, column, or block. A Sudoku has nine of each, making 27 total houses.
Take a look at this sample. You see the two cells with "2" and "3" only? This is a "Naked Pair". 2 and 3 are the only possible candidates for each of those cells.
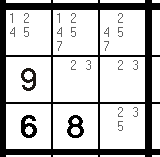
Now notice something else: These two cells are in the same block. So how does this help us? I mean, right now we can't tell which one is the 2 and which is the 3, right?
This is true: we cannot tell which is which. But because Sudoku rules tell us that every block only has only one "2" and only one "3", we can assume that one of them is the 2 and the other is the 3.
Now, this wouldn't help us if there weren't any other "2" or "3" pencil marks in that block. But since there are, we can remove them! The other cells in the block cannot be 2 or 3.
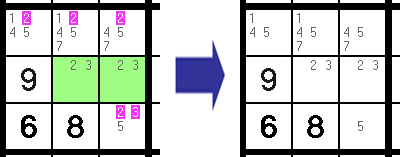
Neat, huh? Notice that by doing this, we have created a Lone Single in the lower right cell (a "5").
By the way, did you notice anything else? Yep! Those two cells are also in the same row. We can use the same principle to remove any 2s and 3s from other cells in that row as well…
The great thing about Naked Pairs is there are relatively easy to spot. This is why they are one of the first things I look for.
Naked Triplets & Quads
Working on the same principle as Naked Pairs, Naked Triplets and Naked Quads can also help us remove candidates (pencil marks) from other cells.
Though not as easy to spot, and also not quite as common, these situations do occur. For example:

See the Naked Triplet? It's the three cells with only 1, 5 & 9 as candidates.
Because all three cells are in the same house, and because their only candidates are 1, 5, or 9; the actual values of these three cells must be 1, 5 & 9.
For the moment, it does not matter which cell is the 1, which is the 5, or which is the 9. It only matters that we know for sure that 1, 5, & 9 go into them somehow.
Which means none of the other cells in the house could possibly be 1, 5, or 9.
Therefore, we can remove those pencil marks from the other cells:

Be careful, though - these guys don't always have all three candidates in all three cells.
For example:

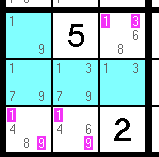
Here, we still have three cells in the same house that can only be one of three candidates.
Can you find them? Hard to see, aren't they?
They are the middle cell and the two cells on each end. Believe it or not, they make up a Naked Triplet. These cells must end up being the 5, 6, & 8, because together they share only those three candidates. The rule still applies - and you can safely remove 5, 6, & 8 from the other cells.
Naked Quads are even more rare, but they do occur on occasion, so they are at least worth mentioning.
See this example:
By the same principal as Naked Triplets and Pairs, the blue cells' only four candidates are 1, 3, 7 & 9. Therefore any other 1, 3, 7 or 9 elsewhere in the block can be removed.
|
9 videos|46 docs
|
FAQs on Identifying Naked Pairs - Master Sudoku: From Beginner to Expert - Class 1
| 1. What are Naked Pairs in Sudoku? |  |
| 2. How do I identify Naked Pairs in a Sudoku puzzle? |  |
| 3. Can Naked Pairs be used in any Sudoku puzzle? |  |
| 4. What is the benefit of using Naked Pairs in solving Sudoku? |  |
| 5. Are there any limitations to using Naked Pairs in Sudoku? |  |





















