Class 6 Exam > Class 6 Notes > Year 6 Mathematics IGCSE (Cambridge) > Chapter Notes: The Number System
The Number System Chapter Notes | Year 6 Mathematics IGCSE (Cambridge) - Class 6 PDF Download
Place value

- The objective is to explain the value of each digit in numbers with up to 3 decimal places.
- Multiply and divide whole numbers and decimals by 10, 100, 1000.
- Compose, decompose, and regroup numbers with up to 3 decimal places.
- Numbers are used daily for tasks like telephoning (digits), calculating prices (decimals), and measuring temperatures (positive and negative numbers).
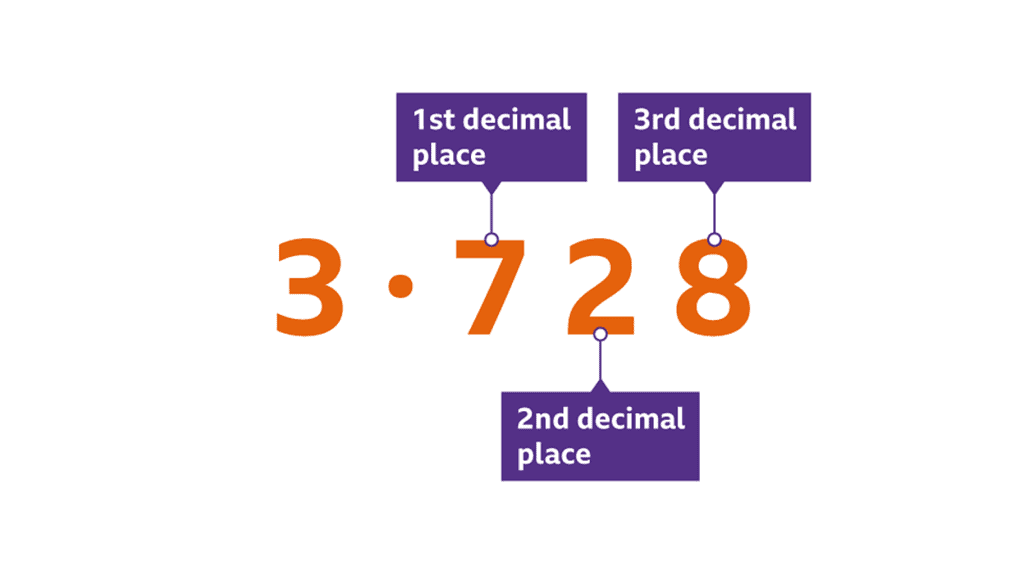
- Each digit’s value depends on its position in a number.
- Whole number positions (from right): ones, tens, hundreds, thousands, etc.
- Decimal positions (from decimal point): tenths (1/10), hundredths (1/100), thousandths (1/1000).
- Example: In 809.46, the digit 9 is in the ones place, worth 9; in 2021.89, 9 is in the hundredths place, worth 0.09.
Composing numbers
- Combine place values to form a number, e.g., 10 + 3 + 1/10 + 3/100 + 6/1000 = 13.136.
- Write digits in a place value grid, aligning them by position (thousands, hundreds, tens, ones, tenths, hundredths, thousandths).
Decomposing numbers
- Break a number into its place value components, e.g., 37.844 = 30 + 7 + 0.8 + 0.04 + 0.004.
Regrouping numbers
- Rearrange digits to represent the same number differently, e.g., 0.546 = 0.4 + 0.14 + 0.006.
Multiplying by 10, 100, 1000
- Shifts digits left (decimal point moves right): 7.2 × 1000 = 7200, 0.85 × 100 = 85, 4.28 × 10 = 42.8.
- Example: 0.01 × 10 = 0.1 (ten times bigger than 0.01).
Dividing by 10, 100, 1000
- Shifts digits right (decimal point moves left): 670 ÷ 100 = 6.7, 151 ÷ 1000 = 0.151, 5.5 ÷ 10 = 0.55.
- Example: 555 ÷ 100 = 5.55 (one hundred times smaller than 555).
- Reverse process: If dividing by 10 three times yields 0.005, the original number is 0.005 × 10 × 10 × 10 = 5.
Rounding decimal numbers
- The objective is to round a number with 2 decimal places to the nearest whole number.
- Round a number with 2 decimal places to the nearest tenth.
- Rounding simplifies numbers for easier understanding, e.g., Usain Bolt’s 100 m time of 9.63 seconds is rounded to 10 seconds.
Rounding to the nearest whole number
- If the tenths digit is 0, 1, 2, 3, 4, round down (keep the whole number part), e.g., 6.2 ≈ 6, 4.09 ≈ 4.
- If the tenths digit is 5, 6, 7, 8, 9, round up (increase the whole number by 1), e.g., 36.5 ≈ 37, 7.89 ≈ 8.
- Example: Smallest number with 1 decimal place rounding to 100 is 99.5; largest rounding to 10 is 10.4.
Rounding to the nearest tenth
- If the hundredths digit is 0, 1, 2, 3, 4, round down (keep the tenths digit), e.g., 8.80 ≈ 8.8, 7.81 ≈ 7.8.
- If the hundredths digit is 5, 6, 7, 8, 9, round up (increase the tenths digit by 1), e.g., 6.45 ≈ 6.5, 3.95 ≈ 4.0.
- Answer always has 1 decimal place, even if it is zero, e.g., 4.0.
- Example: Numbers rounding to 7.5 include 7.45, 7.49, 7.50, 7.51, 7.53, 7.55, 7.56.
The document The Number System Chapter Notes | Year 6 Mathematics IGCSE (Cambridge) - Class 6 is a part of the Class 6 Course Year 6 Mathematics IGCSE (Cambridge).
All you need of Class 6 at this link: Class 6
|
63 docs|17 tests
|
FAQs on The Number System Chapter Notes - Year 6 Mathematics IGCSE (Cambridge) - Class 6
| 1. What is the place value of a digit in a number? |  |
Ans. The place value of a digit in a number refers to its position in the number, which determines its value based on the base of the number system. For example, in the number 345, the digit 3 is in the hundreds place, so its place value is 300. The place value system helps us understand the significance of each digit in a number.
| 2. How do you round decimal numbers? |  |
Ans. Rounding decimal numbers involves adjusting the number to a specified place value. To round a number, you look at the digit immediately to the right of the target digit. If this digit is 5 or greater, you round up; if it is less than 5, you round down. For instance, if you round 3.76 to the nearest tenth, you look at the hundredths place (6) and round up to 3.8.
| 3. What are some examples of rounding numbers in everyday life? |  |
Ans. Rounding numbers is commonly used in various everyday situations, such as estimating costs while shopping, simplifying data for reports, or when calculating time. For instance, if a product costs $19.99, it might be rounded to $20 for simplicity. Similarly, if someone takes 45.6 minutes to complete a task, it may be rounded to 46 minutes.
| 4. Why is understanding place value important in mathematics? |  |
Ans. Understanding place value is crucial because it forms the foundation for performing arithmetic operations, understanding larger numbers, and working with decimals. It helps in distinguishing between numbers like 120 and 102, where the position of each digit significantly affects the overall value. This knowledge is essential for mastering more complex mathematical concepts.
| 5. Can you provide an example of how to use place value to add two numbers? |  |
Ans. Certainly! Let's add the numbers 234 and 567 using place value. We align the numbers vertically by their place values:
234
+ 567
------
Starting from the right, we add the units (4 + 7 = 11), write down 1 and carry over 1. Next, we add the tens (3 + 6 + 1 (carry) = 10), write down 0 and carry over 1. Finally, we add the hundreds (2 + 5 + 1 (carry) = 8). The result is 801.
Related Searches





















