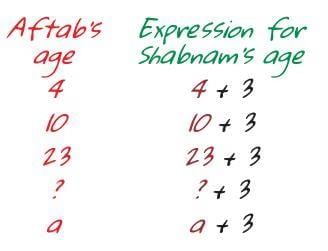Expressions Using Letter-Numbers Class 7 Notes Maths Chapter 4 Free PDF
The Notion of Letter-Numbers
"Why do we need to use letters in math? Numbers make sense, but letters?" Ravi asked his friend Meena as they walked home from school. Meena smiled, remembering how she had the same question last year. Ravi is asking to Meena
Ravi is asking to Meena
"Let me show you something interesting," Meena replied. "Think about Shabnam and Aftab from our class. Shabnam is 3 years older than Aftab, right?"
Shabnam’s age = Aftab’s age + 3.
Ravi nodded, unsure where this was going.
"So if Aftab is 12 years old now, Shabnam is..."
"15," Ravi answered quickly.
"And if Aftab were 20, Shabnam would be..."
"23," said Ravi.
"What if we don't know Aftab's exact age, but still want to talk about Shabnam's age?"
Meena asked. "That's where letters come in!
If we call Aftab's age 'a',
then, Shabnam's age is always 'a + 3'.
Ravi's eyes widened with understanding. "So letters are like... placeholders for numbers that can change or that we don't know yet?" Ravi is happy now.
Ravi is happy now.
"Exactly!" Meena exclaimed. "And when we use letters with numbers and operations, we create what mathematicians call 'algebraic expressions'."
In this Chapter,
- We'll explore how letters can represent numbers and how we can use them to write expressions that describe patterns, relationships, and real-world situations.
- We'll learn how to work with these expressions, evaluate them when we know the values of the letters, and simplify them to make them easier to understand and use.
Example 1: Shabnam is 3 years older than Aftab. When Aftab’s age is 10 years, Shabnam’s age is 13 years. Now Aftab’s age is 18 years. What will Shabnam’s age be?
Sol: We know Shabnam’s age is always Aftab’s age plus 3 years.
Shabnam’s age = Aftab’s age + 3.
Now Aftab is 18 years old.So Shabnam’s age = 18 + 3 = 21 years.
Example 2: Parthiv was playing with matchsticks and noticed something interesting when he made L-shaped patterns:

Sol:
1 L needs 2 matchsticks.
2 Ls need 2 × 2 = 4 matchsticks.
5 Ls need 2 × 5 = 10 matchsticks.
45 Ls need 2 × 45 = 90 matchsticks.
We notice that the number of matchsticks is always 2 times the number of Ls.
To write this in math language, we use a variable. A variable is just a letter that stands for a number. Let’s use:
n = number of L's
Then,Number of matchsticks = 2 × n
Example 3: Rani went to the market to buy coconuts and jaggery. Each coconut costs ₹35, and jaggery costs ₹60 per kilogram. If she buys 'c' coconuts and 'j' kilograms of jaggery, her total cost can be expressed as:
Sol: If you want to buy:
10 coconuts → cost = 10 × ₹35 = ₹350
5 kg jaggery → cost = 5 × ₹60 = ₹300
So, the total cost = ₹350 + ₹300 = ₹650Instead of calculating each time, you can create a formula (algebraic expression):
Let:
c = number of coconuts
j = number of kilograms of jaggery
Expression:
Total cost = c × 35 + j × 60
Example 4: The perimeter of a shape is the total length around it. For a square, all four sides are equal in length.
Sol: If one side is q cm, then:
The perimeter = q + q + q + q = 4 × q
This is written as an algebraic expression:
Perimeter = 4 × q, where q is the length of one side.
If the side of the square is 7 cm, then:
Perimeter = 4 × 7 = 28 cm
Revisiting Arithmetic Expressions
Before we dive deeper into algebraic expressions, let's quickly review what we know about arithmetic expressions.
An arithmetic expression is a combination of numbers and operations (addition, subtraction, multiplication, division). For example:
- 5 + 3
- 10 - 4
- 6 × 2
- 15 ÷ 3
- (8 + 2) × 3
When evaluating arithmetic expressions, we follow the order of operations (sometimes remembered as BODMAS or PEMDAS):
- Brackets (or Parentheses)
- Orders (or Exponents)
- Division and Multiplication (from left to right)
- Addition and Subtraction (from left to right)
For Example, to evaluate 2 + 3 × 4:
- First, we do the multiplication: 3 × 4 = 12
- Then, we do the addition: 2 + 12 = 14
But if we have (2 + 3) × 4:
- First, we evaluate what's in the brackets: (2 + 3) = 5
- Then, we do the multiplication: 5 × 4 = 20
Algebraic expressions follow these same rules, but they include letter-numbers (variables) as well as regular numbers.
Evaluating Algebraic Expressions
When we know the value of the letter-numbers in an algebraic expression, we can substitute those values and evaluate the expression just like an arithmetic expression.
Let's evaluate the expression 3n + 5 when n = 4:
Substitute n = 4 into the expression: 3(4) + 5
Multiply: 12 + 5
Add: 17
Let's try another one. Evaluate 2p - 7 when p = 10:
Substitute p = 10 into the expression: 2(10) - 7
Multiply: 20 - 7
Subtract: 13
Omission of the Multiplication Symbol in Algebraic Expressions
Look at the pattern:
4, 8, 12, 16, 20, 24, 28, ...
This is a list of multiples of 4, which means each number is 4 multiplied by another number.
3rd term = 4 × 3 = 12
29th term = 4 × 29 = 116
To get the nth term of this pattern, the expression is: 4 × n
But in algebra, we don’t usually write the × sign. Instead, we just write them together like this: 4n
More Examples
7k means 7 × k
If k = 4, then 7k = 7 × 4 = 28
5m + 3 means:
First, multiply 5 × m
Then add 3
- If m = 2, then:
5 × 2 + 3 = 10 + 3 = 13
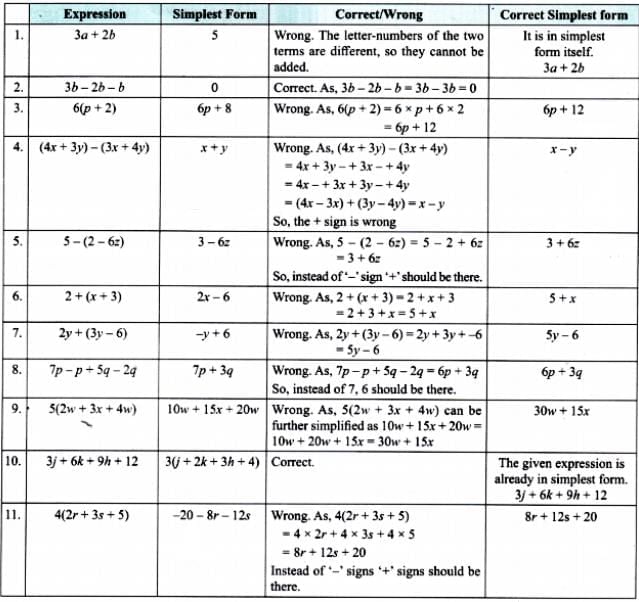
Mind the Mistake, Mend the Mistake
This activity is called "Mind the Mistake, Mend the Mistake". It helps you practice algebra by identifying and fixing mistakes in evaluating expressions when values are substituted.
Let’s go through each and spot the mistakes: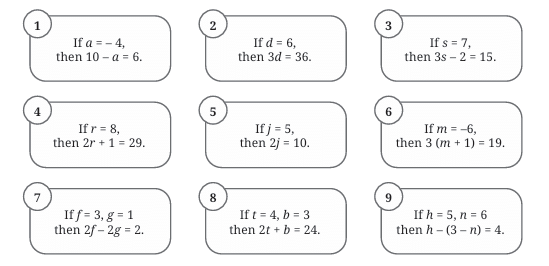
1. If a = 4, then 10 - a = 6.
Ans:
→ 10 - 4 = 6
Hence , Correct
2. If d = 6, then 3d = 36.
Ans:
3d = 3 × 6 = 18, not 36
Hence, Incorrect.
3. If s = 7, then 3s - 2 = 15.
Ans:
3 × 7 - 2 = 21 - 2 = 19, not 15
Hence, Incorrect
4. If r = 8, then 2r + 1 = 29
Ans:
2 × 8 + 1 = 16 + 1 = 17, not 29
Hence, Incorrect
5. If j = 5, then 2j = 10.
Ans: 2 x 5 = 10
Hence, Correct
6. If m = -6, then 3(m + 1) = 19.
Ans: m + 1 = -6 + 1 = -5
3 × (-5) = -15, not 19
Hence, Incorrect
7. If t = 4, b = 3 then 2t + b = 24.
Ans: 2 × 4 + 3 = 8 + 3 = 11, not 24
Hence, Incorrect
8. If h = 5, n = 6, then h - (3 - n) = 4
Ans: 5 − (3 − 6) = 5 − (-3) = 5 + 3 = 8, not 4
Hence , Incorrect
Simplification of Algebraic Expressions
1. Perimeter of a Rectangle Using Expressions
Perimeter formula: Add all sides of the rectangle
p = l + b + l + b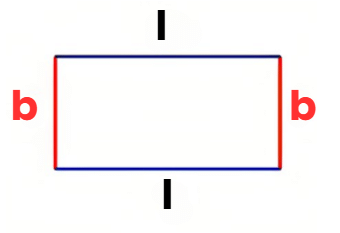
We can rearrange it using properties of addition:
p = 2l + 2b (This is the simplified form)
Example: If length (l) = 3 cm and breadth (b) = 4 cm
Sol: p = l + b + l + b = 3 + 4 + 3 + 4 = 14
p = 2l + 2b = 2 × 3 + 2 × 4 = 6 + 8 = 14
Both give the same result, so they are equivalent expressions.
Expressions from a Word Problem
Example: Here is a table showing the number of pencils and erasers sold in a shop. The price per pencil is c, and the price per eraser is d. Find the total money earned by the shopkeeper during these three days.
Suppose the price of a pencil is c rupees and that of an eraser is d rupees.
A table gives the number of pencils and erasers sold over 3 days:
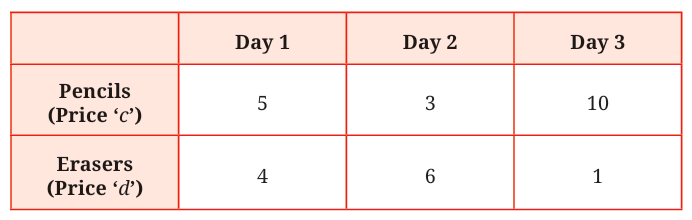
Expression for pencils:
Day 1: 5c, Day 2: 3c, Day 3: 10c
Total = 5c + 3c + 10c
Using distributive property:
= (5 + 3 + 10) × c = 18c
If c = ₹50, then total = 18 × 50 = ₹900
Expression for erasers:
Day 1: 4d, Day 2: 6d, Day 3: 1d
Total = 4d + 6d + 1d = 11d
Combined expression for total sales:
18c + 11d (This is already simplified)
Area of a Big Rectangle
Example: A large rectangle is split into two smaller ones with widths 4 and 3, and the same height (v).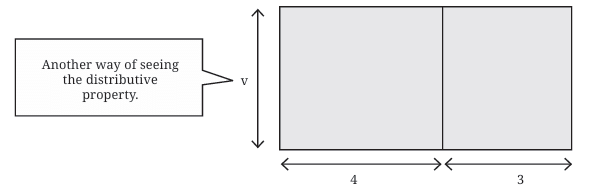 Area of big rectangle:
Area of big rectangle:
- Way 1: Area = v × (4 + 3) = 7v
- Way 2: Area = 4v + 3v = 7v
This shows the distributive property:
v(4+3) = 4v + 3v
AEFD Rectangle Area Expression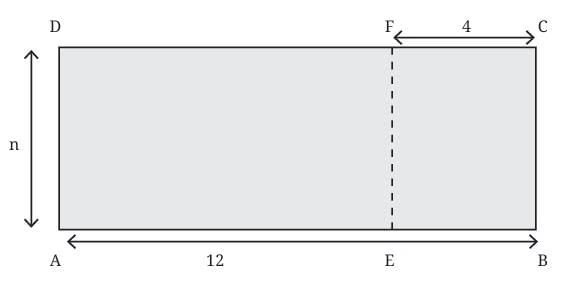
- A large rectangle ABCD is split into AEFD and EBCF.
- Total length AB = 12 units, EB = 4 units, so AE = 12 – 4 = 8 units.
- Height = n
Area of AEFD:
- Way 1: Area = n × 8 = 8n
- Way 2: Area = n × 12 – n × 4 = 12n – 4n = 8n
Conclusion: Both methods give the same answer using different algebraic approaches.
Like Terms vs. Unlike Terms
- Like Terms: Same variable (e.g., 5c, 10c, 18c)
- Unlike Terms: Different variables or powers (e.g., 18c, 11d)
- Like terms can be added together, unlike terms cannot.
Combining Like Terms
To simplify an expression, we combine like terms by adding or subtracting their coefficients (the numbers in front of the letter-numbers).
Let us discuss combination of like terms through addition
Example 1: Simplify 5c + 3c + 10c
Ans: All terms have the letter c, so they are like terms.
5c + 3c + 10c = (5 + 3 + 10)c = 18c
Example 2: Simplify 4v + 3v
Ans: Both terms have the letter v, so they are like terms.
4v + 3v = (4 + 3)v = 7v
Example 3: Simplify l + b + l + b (perimeter of a rectangle)
Ans: The like terms are l and l, and b and b.
l + b + l + b = (l + l) + (b + b) = 2l + 2b
Simplification Involving Subtraction
Example 1: Simplify 8x - 3x
Ans: Both terms have the letter x, so they are like terms.
8x - 3x = (8 - 3)x = 5x
Example 2: Simplify 12y - 5y + 2y
Ans: All terms have the letter y, so they are like terms.
12y - 5y + 2y = (12 - 5 + 2)y = 9y
Simplification Involving Brackets
When a minus sign is placed before brackets, it changes the sign of each term inside the brackets when we remove the brackets.
Example: Simplify 7a - (3a + 2)
Ans: 7a - (3a + 2)
= 7a - 3a - 2
= (7 - 3)a - 2
= 4a - 2
Example: Simplify 5b - (b - 4)
Ans: 5b - (b - 4)
= 5b - b + 4
= (5 - 1)b + 4
= 4b + 4
Mind the Mistake, Mend the Mistake
Pick Patterns and Reveal Relationships
What is a Number Machine?
A number machine takes two input numbers and performs a specific rule or operation on them to produce an output. You need to observe the pattern or rule used to calculate the result and write that as a mathematical expression (also called a formula).
Formula Detective
In the top row of machines, you are given two inputs and one output. Find out the formula of this number machine and solution for the last blank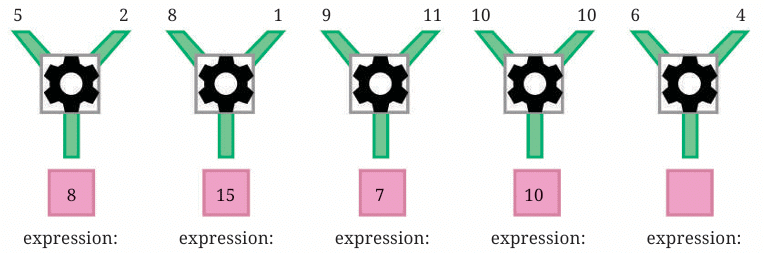
Sol: The formula for the number machine above is “two times the first number minus the second number”.
When written as an algebraic expression, the formula = 2a-b.
The expression for the first set of inputs is 2 × 5 – 2 = 8.
The formula holds for each set of inputs.
Hence the solution for the last blank = 2 × 6 – 4 = 8
Algebraic Expressions to Describe Patterns
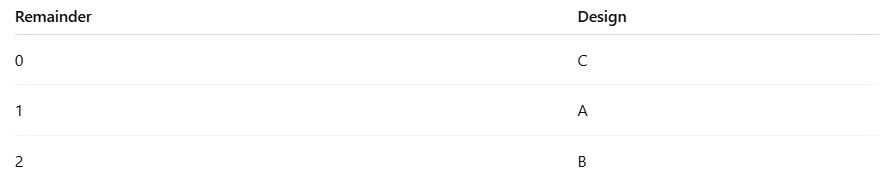
Somjit saw a repeating pattern along the border of a saree. The designs appear in the following order:
These three designs (A, B, C) are repeated again and again in the same sequence. This is called a repeating pattern.
We can see that:
- Every 3rd position is Design C
- Every position 1 less than a multiple of 3 is Design B
- Every position 2 less than a multiple of 3 is Design A
Design C:
It appears at positions: 3, 6, 9, 12, ...These are multiples of 3, which means:
C appears at position:
3n (where n is 1, 2, 3, …)
Design B:
It appears at positions: 2, 5, 8, 11, ...That is always 1 less than C, so:
B appears at position:
3n − 1
Design A:
It appears at positions: 1, 4, 7, 10, ...That is 2 less than C, so:
A appears at position:
3n − 2
Using Division to Quickly Find the Design at Any Position
If someone gives you a random number like 99, how will you know which design it is?
You use division and remainders:
Divide the number by 3
Look at the remainder
Example: Position 99
99 ÷ 3 = 33 remainder 0
→ Remainder is 0 → So, it’s Design C
Example: Position 122
122 ÷ 3 = 40 remainder 2
→ Remainder is 2 → So, it’s Design B
Example: Position 148
148 ÷ 3 = 49 remainder 1
→ Remainder is 1 → So, it’s Design A
Patterns in a Calendar
Here is the calendar of November 2024. Consider 2 × 2 squares, as marked in the calendar. The numbers in this square show an interesting property.
Let us take the marked 2 × 2 square.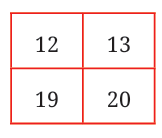 2 × 2
2 × 2
Diagonal Sum Property
Take the diagonals of this 2 × 2 square:
- First diagonal: 12 + 20 = 32
- Second diagonal: 13 + 19 = 32
Observation: Both diagonals add up to the same total!
Let’s prove it works for any number. Let’s call the top-left number a. Then the square is:
Now check the diagonals:
- First diagonal = a + (a + 8) = 2a + 8
- Second diagonal = (a + 1) + (a + 7) = 2a + 8
Both diagonals are equal. This pattern will always hold!
A Plus-Shaped Pattern in the Calendar
Let’s take another shape like a plus sign, using this pattern of numbers: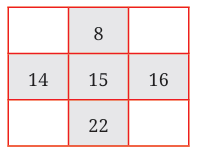
Add up all the numbers:
8 + 14 + 15 + 16 + 22 = 75
Now look at the center number: 15
5 × 15 = 75
Observation: The sum of all 5 numbers is always 5 times the center number.
Why Does This Happen?
Let’s say the center number is a. Then the other numbers are:
- One above: a − 7
- One below: a + 7
- One left: a − 1
- One right: a + 1
Now sum: (a - 7) + (a + 7) + (a - 1) + (a + 1) + a = 5a
The pattern is algebraically proven — no matter which number is in the center, the total will be 5 × center number!

Matchstick Patterns
You are given a series of patterns made by arranging triangles using matchsticks. Each triangle shares a side with the next one.
Look at the image given above:
- Step 1 has 1 triangle.
- Step 2 has 2 triangles.
- Step 3 has 3 triangles.
- And so on…
So what’s changing? The number of matchsticks.
How many matchsticks are used?
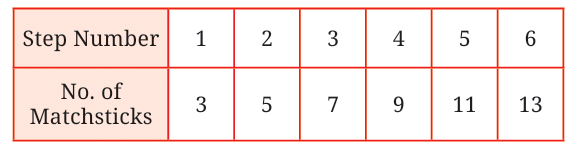
- Step 1 → 3 matchsticks
- Step 2 → 5 matchsticks
- Step 3 → 7 matchsticks
- Step 4 → 9 matchsticks
- Step 5 → 11 matchsticks
What do we observe?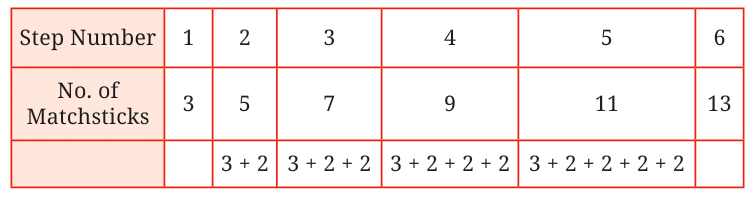
Each new triangle adds 2 more matchsticks.
So the number of matchsticks increases by 2 every time.
Let’s use Algebra Now
Let’s say the step number is y. We want a rule (or formula) to find the number of matchsticks at any step.
From the pattern:
Step 1 → 3 matchsticks = 1 + 2
Step 2 → 3 + 2 = 5
Step 3 → 3 + 2 + 2 = 7
Step 4 → 3 + 2 + 2 + 2 = 9
So the general formula becomes:
Matchsticks = 3 + 2 × (y − 1)
Now let’s simplify this expression:
3 + 2 × (y − 1)
= 3 + 2y − 2
= 2y + 1
Let’s use this formula for:
Step 33
2 × 33 + 1 = 66 + 1 = 67 matchsticksStep 84
2 × 84 + 1 = 168 + 1 = 169 matchsticksStep 108
2 × 108 + 1 = 216 + 1 = 217 matchsticks
Two orientations of matchsticks
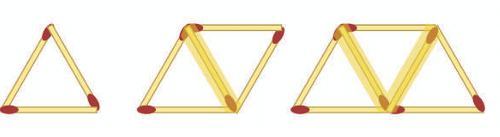 In each triangle:
In each triangle:
- There are horizontal matchsticks (top and bottom)
- And diagonal matchsticks (middle)
For example: In Step 2:
- Horizontal: 2
- Diagonal: 3
Check Step 3 to see how this changes.
- Horizontal: 3
- Diagonal: 4
→ Total = 7
You can write two expressions—one for horizontal matchsticks and one for diagonal, and their sum should be 2y + 1.
Some Solved Examples
Example 1: Evaluate the expression 4x + 3y when x = 5 and y = 2.
Sol:
Step 1: Substitute the values of x and y into the expression.
4x + 3y = 4(5) + 3(2)
Step 2: Multiply.
4(5) + 3(2) = 20 + 6
Step 3: Add.
20 + 6 = 26
Therefore, when x = 5 and y = 2, the value of 4x + 3y is 26.
Example 2: Simplify the expression 9p - (3p - 4q + 2).
Sol:
Step 1: Remove the brackets, changing the sign of each term inside.
9p - (3p - 4q + 2) = 9p - 3p + 4q - 2
Step 2: Combine like terms.
9p - 3p + 4q - 2 = (9 - 3)p + 4q - 2
= 6p + 4q - 2
Therefore, the simplified expression is 6p + 4q - 2.
Example 3: A rectangular field has length 'l' meters and width 'w' meters. A path of width 2 meters runs around the inside of the field. Write an expression for the area of the path.
Sol:
Step 1: Find the area of the entire field.
Area of field = l × w
Step 2: Find the area of the inner rectangle (field minus path).
Length of inner rectangle = l - 2 - 2 = l - 4 (2 meters less on each side)
Width of inner rectangle = w - 2 - 2 = w - 4 (2 meters less on each side)
Area of inner rectangle = (l - 4) × (w - 4)
= lw - 4l - 4w + 16
Step 3: Find the area of the path by subtracting the inner area from the total area.
Area of path = Area of field - Area of inner rectangle
= lw - (lw - 4l - 4w + 16)
= lw - lw + 4l + 4w - 16
= 4l + 4w - 16
Therefore, the area of the path is 4l + 4w - 16 square meters.
FAQs on Expressions Using Letter-Numbers Class 7 Notes Maths Chapter 4 Free PDF
| 1. What are letter-numbers in the context of algebra? |  |
| 2. How can I simplify algebraic expressions effectively? |  |
| 3. Why is the multiplication symbol often omitted in algebraic expressions? |  |
| 4. Can you explain how to revisit arithmetic expressions in algebra? |  |
| 5. What types of practice exercises can help me understand expressions using letter-numbers? |  |