A Tale of Three Intersecting Lines Class 7 Notes Maths Chapter 7 Free PDF
Introduction
Have you ever looked closely at the world around you? From the slice of cheese you eat to the towering bridges you cross, shapes are everywhere!
One of the most fundamental and fascinating shapes is the triangle. It might seem simple, just three lines meeting at three points, but this basic shape holds a surprising amount of depth and is the building block for many complex structures.
A triangle, in its essence, is the most basic closed shape you can make with straight lines. It's defined by three key components:
Vertices: These are the three corner points where the lines meet.
Sides: These are the three straight line segments that connect pairs of vertices, forming the boundary of the triangle.
Angles: Formed at each vertex where two sides meet, a triangle has three internal angles.
Let's dive deeper into the world of triangles!
Understanding Triangles
As we discovered, a triangle is the most fundamental closed shape formed by three straight lines. Let's break down its core components:
A triangle is defined by:
Three Vertices: These are the corner points where the sides intersect. Think of them as the 'tips' of the triangle.
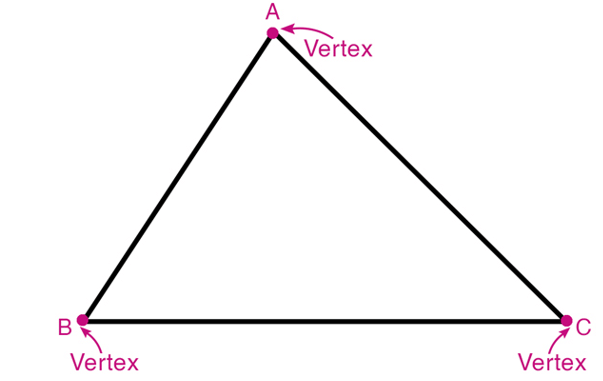
Three Sides: These are the straight line segments connecting each pair of vertices. They form the boundary of the triangle.
Triangles can look very different! Some are tall and skinny, some are wide, and some have all sides the same length. Here are a few examples:
Naming Triangles
We usually name triangles using their vertices. For example, if a triangle has vertices labeled A, B, and C, we call it ∆ABC. The symbol ∆ is shorthand for "triangle".
When naming a triangle, the order of the vertices doesn't matter. So, ∆ABC is the same triangle as ∆BCA, ∆CAB, ∆CBA, ∆BAC, or ∆ACB. We just need to use the three vertex letters.
Angles of a Triangle
The three sides meeting at the vertices also create three angles inside the triangle. For ∆ABC, the angles are ∠CAB (the angle at vertex A), ∠ABC (the angle at vertex B), and ∠BCA (the angle at vertex C). Often, we simplify this and just call them ∠A, ∠B, and ∠C.

A triangle is a shape with three straight sides and three corners (vertices), where the sides connect to form a closed shape.
Now imagine this:
You have three points (vertices).
But all three points lie on a single straight line (this is called being collinear).
If you try to connect these points, you’ll just get a line segment — not a closed shape.
No, you cannot form a triangle.
Even if you connect all three points, the "shape" you make is just a straight line.
Equilateral Triangles
An equilateral triangle is a triangle in which all three sides are of equal length.
Among all triangles, equilateral triangles stand out for their perfect symmetry.
Because all sides are equal, all angles in an equilateral triangle are also equal (each measuring 60 degrees).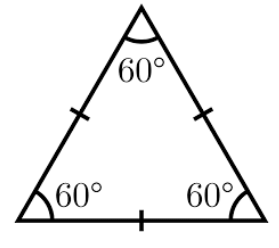
Constructing an Equilateral Triangle
Let's try constructing one! How would you construct a triangle where all sides are exactly 4 cm long?
You could try using just a ruler, drawing a 4 cm base (say, AB) and then trying to position the third vertex (C) so that AC and BC are both 4 cm. However, this often takes a lot of trial and error!
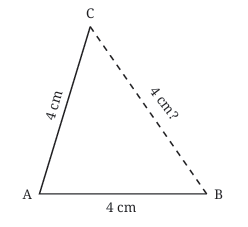
A much more efficient and accurate method uses a compass, similar to constructions you might have done before.
Steps using Ruler and Compass:
Draw the Base: Use your ruler to draw a line segment AB that is 4 cm long.
Draw the First Arc: Place the compass point on vertex A. Adjust the compass width to 4 cm (the desired side length). Draw a long arc above the base line. The third vertex, C, must lie somewhere on this arc because every point on this arc is exactly 4 cm away from A
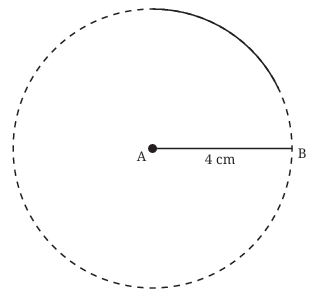
Draw the Second Arc: Now, without changing the compass width (keep it at 4 cm), place the compass point on vertex B. Draw another arc that intersects the first arc. Let the point where the arcs intersect be C.
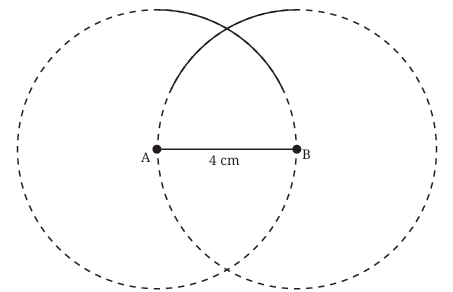
Join the Vertices: Use your ruler to draw straight lines connecting A to C and B to C.
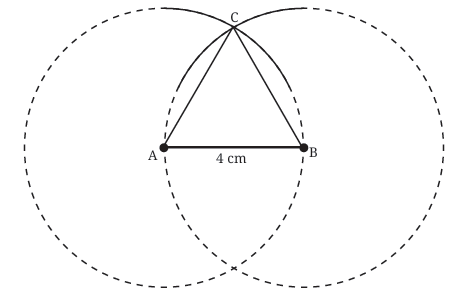 You have constructed an equilateral triangle ∆ABC with all sides equal to 4 cm. The intersection point C is guaranteed to be 4 cm from A (because it's on the first arc) and 4 cm from B (because it's on the second arc).
You have constructed an equilateral triangle ∆ABC with all sides equal to 4 cm. The intersection point C is guaranteed to be 4 cm from A (because it's on the first arc) and 4 cm from B (because it's on the second arc).
Constructing a Triangle When its Sides are Given
Make a triangle with sides 4 cm, 5 cm, and 6 cm.
Steps to Construct the Triangle:
Step 1: Draw the base
Pick one of the side lengths (say 4 cm) and draw a straight line.
Label the ends as A and B.

Step 2: Use your compass
From point A, draw an arc with radius 5 cm. This arc shows all the places where point C (the third corner of the triangle) could be, if it's 5 cm from A.
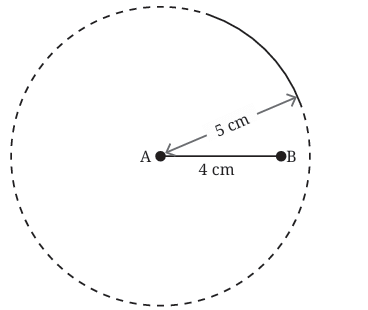
Step 3: Draw another arc
From point B, draw another arc with radius 6 cm. This arc shows where C could be if it’s 6 cm from B.
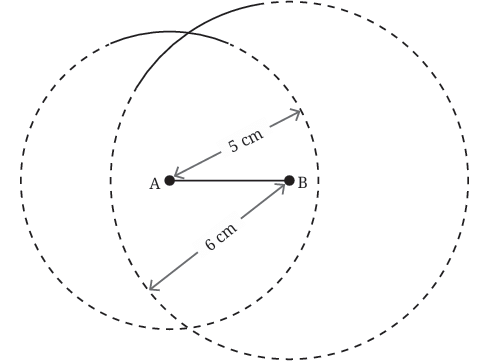
Step 4: Find the point where the arcs meet
The place where the two arcs cross is the point C. This point is exactly 5 cm from A and 6 cm from B — just like we need.

Step 5: Join the points
Now connect A to C and B to C to complete the triangle.
You’ve just drawn a triangle with the exact sides: 4 cm, 5 cm, and 6 cm!
If you try to make a triangle using three points (called vertices), but all of them lie on the same straight line, then you cannot form a triangle. Why?
Because a triangle is a closed shape with three sides. If the points are all on one straight line, they’re said to be collinear, and you can only draw a straight line through them — not a shape with corners and angles. That means you don’t get a “triangle,” just a line.
You need the three points to be in different directions — not just lying flat on the same path — so that the lines connecting them can turn and close up the shape.
Are Triangles Possible for Any Lengths?
This section explores when triangle construction is possible or impossible, introducing the Triangle Inequality Theorem.
Examples given:
Try to make a triangle with side lengths:
(1) 3 cm, 4 cm, and 8 cm
(2) 2 cm, 3 cm, and 6 cm
(3) 10 cm, 15 cm, and 30 cm
When you try these, you’ll notice that:
In all these cases, the sum of the two shorter sides is equal to or less than the third side.
For example: 3 + 4 = 7 < 8 → Not possible
2 + 3 = 5 < 6 → Not possible
10 + 15 = 25 < 30 → Not possible
Triangle Inequality
This is a beautiful real-world illustration:
Imagine walking from a tent to a tree directly (shortest path).
Or walking from the tent to a pole, then from the pole to the tree (longer path).
 Triangle Inequality Example
Triangle Inequality ExampleThis demonstrates: The direct path is always shorter than any indirect one.
So the sum of two sides of a triangle must always be greater than the third side, or the triangle collapses into a line.
Let's have a look on the below given example -
A triangle is possible only if the sum of the lengths of any two sides is greater than the third side.
For example:
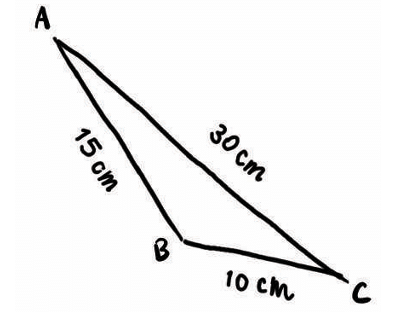
Side lengths: 10 cm, 15 cm, 30 cm
Check:
10 + 15 = 25 < 30 → ❌ Not valid
So, a triangle is not possible with these lengths.
Does everything look right with this triangle?
If this triangle were possible, then the direct path between any two vertices should be shorter than the roundabout path via the third vertex. Is this true for our rough diagram?
1. From B to C
Direct path: BC = 10 cm
Roundabout path via A: BA + AC = 15 cm + 30 cm = 45 cm
✔️ The direct path (10 cm) is shorter than the roundabout path (45 cm) → This is OK.
2. From A to B
Direct path: AB = 15 cm
Roundabout path via C: AC + CB = 30 cm + 10 cm = 40 cm
✔️ The direct path (15 cm) is shorter than the roundabout path (40 cm) → This is OK too.
3. From C to A
Direct path: CA = 30 cm
Roundabout path via B: CB + BA = 10 cm + 15 cm = 25 cm
⛔️ The direct path (30 cm) is longer than the roundabout path (25 cm) → This is not possible in a real triangle!
This situation is not possible in real life. You cannot make a triangle where one side is longer than the sum of the other two sides.
In our example:
30 cm > 10 cm + 15 cm
30 cm > 25 cm → ❌ This breaks the triangle rule!
Visualising the construction of circles
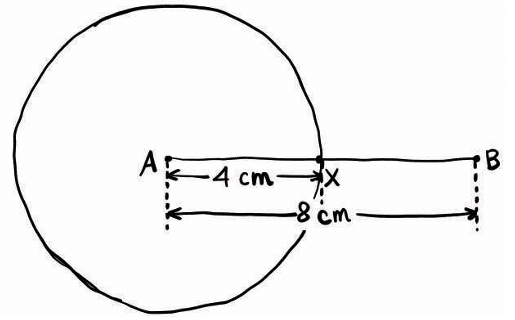
We want to construct a triangle with side lengths:
AB = 8 cm (the longest side),
AX = 4 cm,
BX = 5 cm.
Step 1: Draw the base AB = 8 cm
Use a ruler to draw a straight line 8 cm long.
Label the ends as A and B.
Step 2: Use compass to draw circle with centre A and radius 4 cm
Open your compass to 4 cm.
Place the needle on A, and draw a full circle.
Every point on this circle is 4 cm away from A. This circle shows all the places where point X could be, such that AX = 4 cm.
Step 3: Use compass to draw circle with centre B and radius 5 cm
Open your compass to 5 cm.
Place the needle on B, and draw another full circle.
Every point on this circle is 5 cm away from B. This circle shows all the possible positions of X such that BX = 5 cm.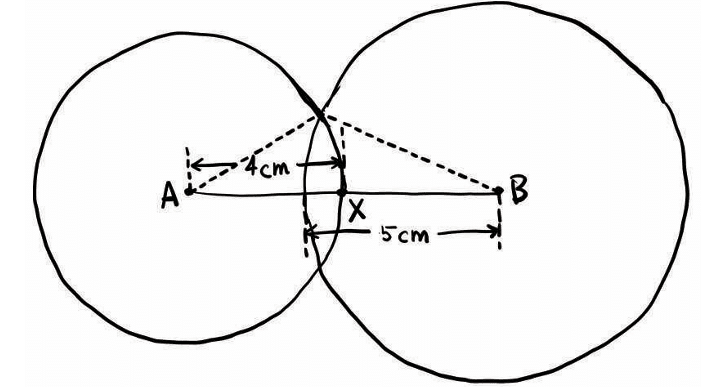 Circles intersecting each other at two points
Circles intersecting each other at two points
What happens when you draw both circles?
The two circles intersect at two points. This means there are two possible positions for point C, which will satisfy both:
AC = 4 cm (from A's circle), and
BC = 5 cm (from B's circle).
So, we can now join A to C and B to C to form the triangle ABC.
Why does this work?
The point of intersection of the two circles is exactly the point that is 4 cm from A and 5 cm from B. So, the triangle ABC will have:
AB = 8 cm (the base),
AC = 4 cm (from the first circle),
BC = 5 cm (from the second circle).
Q: Will triangles always exist when a set of lengths satisfies the triangle inequality? How can we be sure?
Ans: Case 1: Imagine you have two points, A and B, on a piece of paper, and the distance between them is one of the sides of your triangle (let’s call it AB). This side AB is going to be the longest side of the triangle you’re trying to make.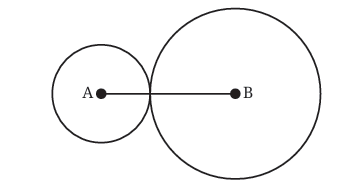 Case 1: Circles touch each other
Case 1: Circles touch each other
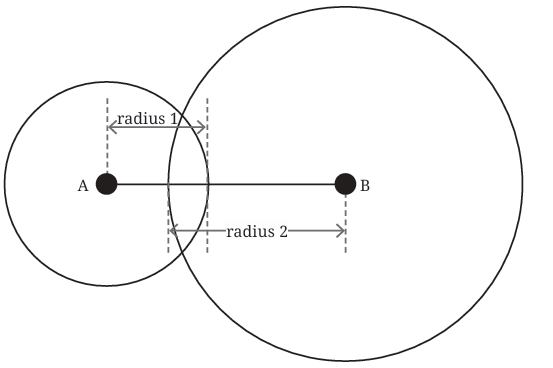
Case 2: The other two sides of the triangle (let’s call them “radius 1” and “radius 2”) are represented by two circles:
- One circle is centered at point A, and its radius (the distance from A to the edge of the circle) is “radius 1.”
- The other circle is centered at point B, and its radius is “radius 2.”
- These two radii (radius 1 and radius 2) are the lengths of the other two sides of the triangle you’re trying to make.
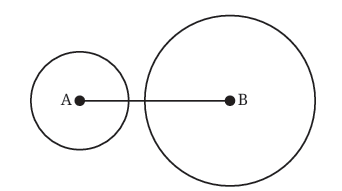 Case 2: Circles do not intersect
Case 2: Circles do not intersect
Can these two circles intersect (cross each other) at a third point, C?
If they do, then point C can be the third corner of your triangle, and you can draw the triangle ABC. If they don’t intersect, you can’t make a triangle.
Case 3: Circles Intersect Internally (Cross Each Other at Two Points)
This is the only case where a triangle can be formed!
The two intersection points of the circles give possible positions for point C, creating the triangle ABC.
Let us study each of these cases by finding the relation between the radii (the smaller two lengths) and AB (longest length).
Case 1: Circles Touch Each Other at a Point
In this case, the two circles just barely touch each other at one spot.
- When the circles touch like this, the distance between A and B (which is the length of side AB) is exactly equal to the sum of the two radii.
- In math terms: radius 1 + radius 2 = AB.
- If we think about the triangle inequality, this means the sum of the two smaller sides (radius 1 and radius 2) is equal to the longest side (AB).
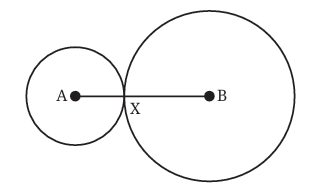
But here’s the problem: when the sum of the two smaller sides is exactly equal to the longest side, the “triangle” you get isn’t really a triangle—it’s a straight line! Imagine points A, B, and C (where the circles touch) all lining up perfectly. That’s not a triangle because a triangle needs to have an inside area, not just be a flat line. So, in this case, a triangle cannot form.
Case 2: Circles do not Intersect internally
In this case, the two circles are too far apart to touch each other.
- When the circles don’t intersect, the distance between A and B (the length of AB) is bigger than the sum of the two radii.
- In math terms: radius 1 + radius 2 < AB.
- If we think about the triangle inequality, this means the sum of the two smaller sides (radius 1 and radius 2) is less than the longest side (AB).
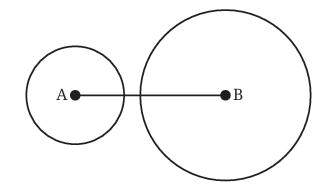
When this happens, the two smaller sides are too short to connect and form a triangle. Imagine trying to build a triangle with two short sticks that can’t even reach the ends of the longest stick—it just won’t work. So, in this case, a triangle cannot form either.
Case 3: Circles intersect each other
In this case, the two circles overlap and cross each other at two points. It’s like the balloons at A and B are big enough to overlap a bit.
- When the circles intersect, the distance between A and B (the length of AB) is less than the sum of the two radii.
- In math terms: radius 1 + radius 2 > AB.
- If we think about the triangle inequality, this means the sum of the two smaller sides (radius 1 and radius 2) is greater than the longest side (AB).
When this happens, the circles intersect at two points, and you can pick one of those points (let’s call it C) to be the third corner of your triangle. Now you can draw a triangle ABC, with sides AB, AC (which is radius 1), and BC (which is radius 2). Since the sum of the two smaller sides is bigger than the longest side, the triangle inequality is satisfied, and a triangle can form!
Conclusion
The triangle inequality says that for any three lengths to form a triangle, the sum of any two sides must be greater than the third side.
From the cases we looked at:
- In Case 1, the sum of the two smaller lengths equals the longest length, so a triangle doesn’t form (it’s a straight line).
- In Case 2, the sum of the two smaller lengths is less than the longest length, so a triangle doesn’t form.
- In Case 3, the sum of the two smaller lengths is greater than the longest length, and a triangle does form.
So, triangles only exist when the sum of the two smaller lengths is greater than the longest length (like in Case 3). If the sum is equal to or less than the longest length (like in Cases 1 and 2), a triangle can’t form.
Construction of Triangles When Some Sides and Angles are Given
Constructing triangles — that means drawing a triangle correctly using some given information.
In this case, we are given:
Two sides of the triangle (AB and AC),
And the angle between them (∠A).
This is called "Two Sides and the Included Angle" because the angle is between the two given sides.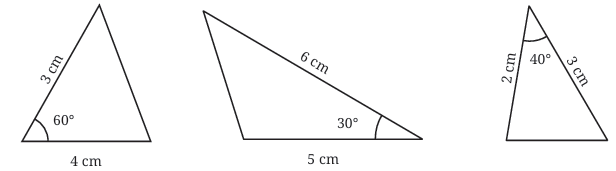
Steps to draw:
We are given:
AB = 5 cm
AC = 4 cm
∠A = 45°
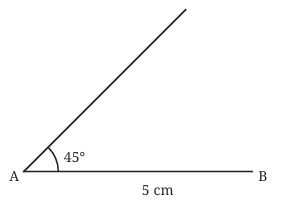
We will draw triangle ABC using these steps:
Draw AB = 5 cm – This is one side of the triangle.
At point A, draw a 45° angle – Use a protractor to do this.
From point A, measure 4 cm along the arm of the angle – Mark this point as C. This is the second side AC = 4 cm.
Join point B to point C – Now you have triangle ABC.
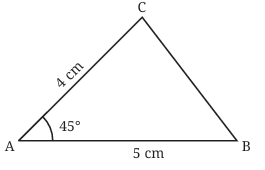
 Minie is confused
Minie is confused
Not always! Here's why:
A triangle must close — the third side (BC) must be able to connect the two arms.
If the angle is too small, and the sides are not long enough, the two lines might not meet.
If the angle is too wide, and one side is short, again the lines may not reach each other.
So, even if you have two sides and an angle, sometimes it's not possible to make a triangle.
Two Angles and the Included Side
What does this mean?
You are given:
Two angles (like ∠A and ∠B),
And the side between them (AB).
This side is called the included side. Triangles with one side and two angles
Triangles with one side and two angles
How to draw the triangle?
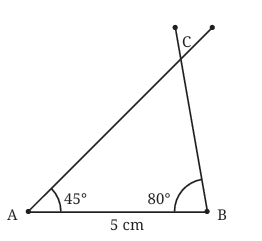
Suppose you're given:
AB = 5 cm
∠A = 45°
∠B = 80°
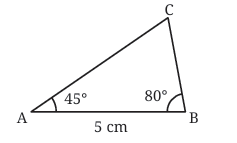
Follow these simple steps:
Draw AB = 5 cm (the given side).
At point A, use a protractor to draw ∠A = 45°.
At point B, draw ∠B = 80°.
The two lines you draw will meet — mark the meeting point as C.
Now, join AC and BC — you have your triangle ABC!
Do triangles always exist with any two angles and a side?
No! Not always. Here's why:
If the two given angles are too big, they might never meet to form a triangle.
For example, if both angles are 90° or more, then the two sides just go straight and never intersect — so, no triangle is formed!

Example:
If one angle is 40°, the second angle (at the other end) must be less than 140°, or else the two lines won’t meet.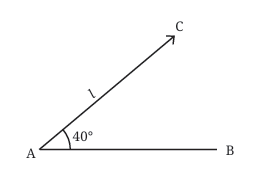
Why 140°?
Because in a triangle, the sum of all three angles must be 180°.
So if angle A is 40°, and you try to make angle B = 140°, the third angle becomes 0°, which is impossible!
And if angle B is more than 140°, the lines go too wide and never meet.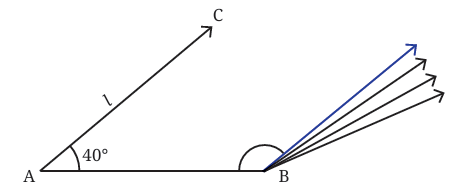
Conclusion:
A triangle does not exist if the sum of the two given angles is greater than or equal to 180°.
Even if you have a side between the angles, it doesn't help if the lines never meet.
Using Parallel Lines
In the diagram given below, a parallel line (XY) is drawn through vertex A to help show that the angles formed with the parallel lines are related to the original angles. This helps in understanding the alternate angles that are equal.
When you draw a line parallel to one side of a triangle, it creates certain relationships between the angles.
For example, alternate angles (the angles on opposite sides of a transversal) are equal.
Step-by-step Example:
In the triangle △ABC, we are given two angles:
∠ABC=50°
∠ACB=70°
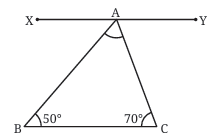
- We want to find ∠BAC.
How to Find ∠BAC:
First, add the known angles: 50°+70°=120°.
Since the sum of the angles in any triangle is 180°, subtract 120° from 180° to get the third angle:
180°−120°=60°.
Therefore, ∠BAC=60°.
Angle Sum Property
The sum of the angles of any triangle is always 180°.
This means that if you know two of the angles in a triangle, you can find the third angle by subtracting the sum of the known angles from 180°.
We need to find ∠A + ∠B + ∠C.
We know that ∠B = ∠XAB, ∠C = ∠YAC.
So, ∠A + ∠B + ∠C = ∠A + ∠XAB + ∠YAC
= 180° as together they form a straight angle.
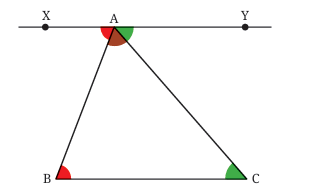 Thus we have proved that the sum of the three angles in any triangle is 180°! This rather surprising result is called the angle sum property of triangles.
Thus we have proved that the sum of the three angles in any triangle is 180°! This rather surprising result is called the angle sum property of triangles.
Parallel Lines to Find Angles: One method to show that the sum of the angles of a triangle is 180° is by using parallel lines. When you draw a line parallel to one side of the triangle, it helps form relationships between the angles.
In the example, the line XY is parallel to the base of the triangle BC, and by using alternate angles, we can prove that the sum of the angles in a triangle is always 180°.
This rule is known as the Angle Sum Property of Triangles. It is a very important property in geometry that helps in solving for unknown angles in a triangle.
Here is an image demonstrates a creative way to verify the Angle Sum Property of a triangle using a paper cut-out. Here's how it works:
Cut out a Triangle: Start by cutting out a triangle from a piece of paper. This triangle represents any triangle, and its angles are the focus.
Folding the Angles: Next, you fold the triangle along its edges. The key idea is to fold each corner (or vertex) of the triangle so that each angle aligns with one another. When you do this, all three angles of the triangle will meet at a single point.
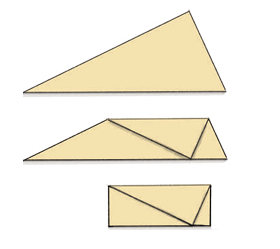
Forming a Straight Line: Once the folds are made, you'll see that the three angles of the triangle come together to form a straight line. This is the key observation: the total amount of space along the straight line is 180°.
This simple folding method shows that the sum of the three angles in a triangle is always 180°. No matter what triangle you use, when you fold the corners together, the angles will always add up to a straight line, which equals 180°.
Exterior Angles
This is the angle formed when you extend one side of a triangle. The exterior angle is always connected to the two interior angles of the triangle.
In the example, ∠ACD is the exterior angle. The key idea here is that the exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles. So, if you know the two interior angles that are not next to the exterior angle, you can find the exterior angle by adding them together.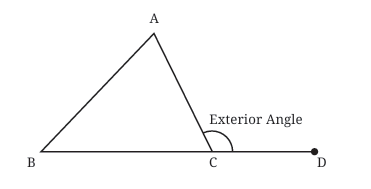
Example:
If ∠A = 50° and ∠B = 60°, you can find the exterior angle ∠ACD by adding these two angles:
∠ACD = 50° + 60° = 110°
This shows that the exterior angle is equal to the sum of the two opposite interior angles.
Example: Can we make a triangle with sides of length 3 cm, 4 cm, and 8 cm?
Sol: We will use the Triangle Inequality Theorem, which states that the sum of the lengths of any two sides of a triangle must always be greater than the length of the third side.
Let's check the triangle inequality for the given side lengths:
3 cm + 4 cm = 7 cm (which is less than 8 cm)
Since 7 cm is less than 8 cm, it’s impossible to form a triangle with sides of 3 cm, 4 cm, and 8 cm.
Constructions Related to Altitudes of Triangles
An altitude is a line drawn from any vertex of a triangle that is perpendicular (at a right angle) to the opposite side (or the line that extends the opposite side).
Height of a Triangle: In everyday life, we talk about the height of things, like the height of a building or a tree. In geometry, the term "height" refers to the perpendicular distance from a vertex of a triangle to the opposite side. This perpendicular line is called the altitude.
How to Draw an Altitude in a Triangle?
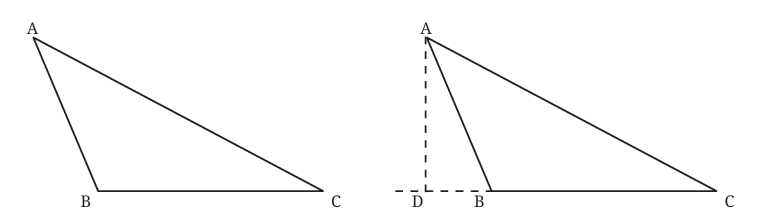
Altitude from Vertex A: In the first image, we have triangle ABC, and we are interested in the altitude from vertex A to side BC.
The line AD is drawn from vertex A perpendicular to BC.
The length of this line, AD, is the altitude of vertex A from the side BC.
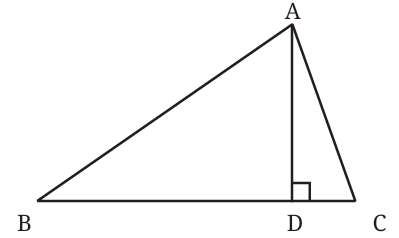
Altitude from Other Vertices: Similarly, we can draw altitudes from the other vertices of the triangle. In the image given below, we can see how altitudes are also drawn from vertices B and C to their respective opposite sides: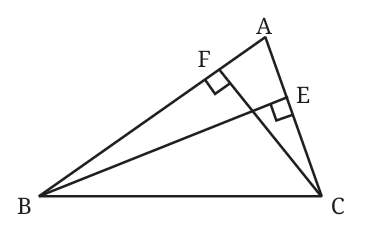
BE is the altitude from vertex B to side AC. CF is the altitude from vertex C to side AB.
How Altitudes Change with Different Triangles
In right-angled triangles, the altitude from the right angle vertex will be the line along the height of the triangle.
In acute triangles (all angles less than 90°), altitudes are drawn inside the triangle.
In obtuse triangles (one angle greater than 90°), altitudes might need to be extended outside the triangle, as seen in the figure given below. This is shown by extending the side BC and drawing a perpendicular from A to this extended line.
Construction of the Altitudes of a Triangle
Let's imagine we have a triangle, and we want to find the altitude from vertex A to the base BC. Here's how we can do it:
Start with the triangle: Label the vertices as A, B, and C, with BC being the base.
Using a ruler and set square: A set square is a tool that helps you make sure you have a perfect right angle (90°). If you just use a ruler, the line may not be exactly 90°, and that's not good for our altitude. The set square helps us be accurate!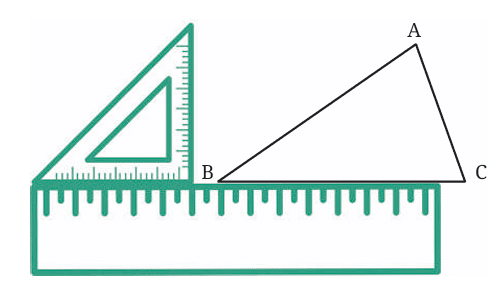
Aligning the ruler and set square:
Place the ruler along the base BC.
Put the set square on the ruler so that one of its right-angle edges is touching the ruler. This way, we’re guaranteed that one side of the set square forms a perfect 90° angle.
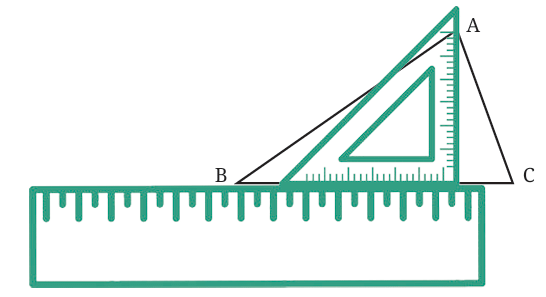
Sliding the set square: Now, move the set square along the ruler until the vertical edge of the set square touches vertex A. This will be the point from which the altitude is drawn.
Draw the altitude: Using the vertical edge of the set square, draw a straight line from A straight down to the base BC. This line is your altitude!
What Happens if One Side is the Altitude?
Now, you might wonder, “Can a side of a triangle also be an altitude?” 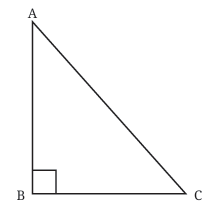 The answer is yes, but this happens only in a right-angled triangle. In a right triangle, one of the sides already makes a 90° angle, so that side can also be the altitude. This is special because in other triangles, the altitude is always a separate line.
The answer is yes, but this happens only in a right-angled triangle. In a right triangle, one of the sides already makes a 90° angle, so that side can also be the altitude. This is special because in other triangles, the altitude is always a separate line.
Types of Triangles
Types of Triangles Based on Sides
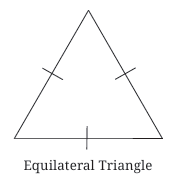
Equilateral Triangle:
All three sides are equal in length.
All three angles are also equal, and each angle measures 60°.
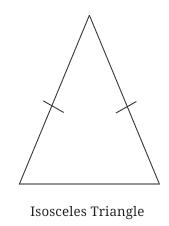
Isosceles Triangle:
Two sides are equal in length.
The two angles opposite these equal sides are also equal.
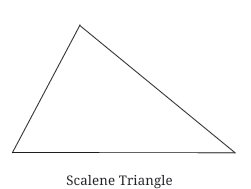
Scalene Triangle:
All three sides have different lengths.
All three angles are different from each other.
Right-Angled Triangle:
One of the angles is exactly 90° (a right angle).
The other two angles are acute (less than 90°).
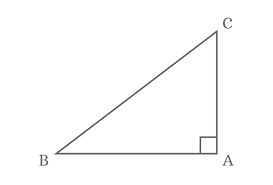 Right-angled Triangle
Right-angled Triangle
Types of Triangles Based on Angles
Triangles can also be classified based on their angle measures. These are:
Acute-Angled Triangle:
All three angles are acute (less than 90°).
In other words, every angle in this triangle is greater than 0° but less than 90°.
Right-Angled Triangle:
One of the angles is exactly 90° (a right angle).
Obtuse-Angled Triangle:
One of the angles is obtuse (greater than 90° but less than 180°).
The other two angles will be acute because the total sum of angles in any triangle must always be 180°.

Is There a Connection Between the Two Classifications?
Yes, there is a connection between the two classifications!
Equilateral triangles are always acute-angled triangles because all their angles are 60°, which is an acute angle.
Isosceles triangles can be of any type based on angles:
If the two equal angles are both less than 90°, it’s an acute-angled isosceles triangle.
If one angle is 90°, it’s a right-angled isosceles triangle.
If one angle is greater than 90°, it’s an obtuse-angled isosceles triangle.
Scalene triangles can also be classified by angles:
If all three angles are less than 90°, it’s an acute-angled scalene triangle.
If one angle is 90°, it’s a right-angled scalene triangle.
If one angle is greater than 90°, it’s an obtuse-angled scalene triangle.
What about Acute-Angled Triangles?
In an acute-angled triangle, all three angles are acute (less than 90°). So, it’s not just a triangle with one acute angle – it has all three angles being acute. This is important because it means every angle is small, but the sum of them still equals 180°.
FAQs on A Tale of Three Intersecting Lines Class 7 Notes Maths Chapter 7 Free PDF
| 1. What is the Triangle Inequality Theorem? |  |
| 2. How can I construct a triangle using the Side-Side-Side (SSS) method? |  |
| 3. What are the special types of triangles? |  |
| 4. Can any three lengths form a triangle? |  |
| 5. What are some practical applications of triangles in real life? |  |