NCERT Solutions for Class 7 Maths Chapter 7 A Tale of Three Intersecting Lines
Page No. 146
Q: What happens when the three vertices lie on a straight line?
Ans: When the three vertices lie on a straight line, they become collinear. This means they no longer form a triangle because the three points do not enclose any area; they simply align along the same straight path.
Page No. 150
Q: Construct triangles having the following sidelengths (all units in cm):
(a) 4, 4, 6;
(b) 3, 4, 5;
(c) 1, 5, 5;
(d) 4, 6, 8;
(e) 3.5, 3.5, 3.5
Ans:
(a) Steps of Construction:
Step 1: Construct the base AB with one of the side lengths.
Let us choose AB = 6 cm.
Step 2: From A, construct a long arc of radius 4 cm.
Step 3: From B, construct an arc of radius 4 cm such that it intersects the first arc.
Step 4: The point where both the arcs meet is the required third vertex C.
Join AC and BC to get ∆ABC.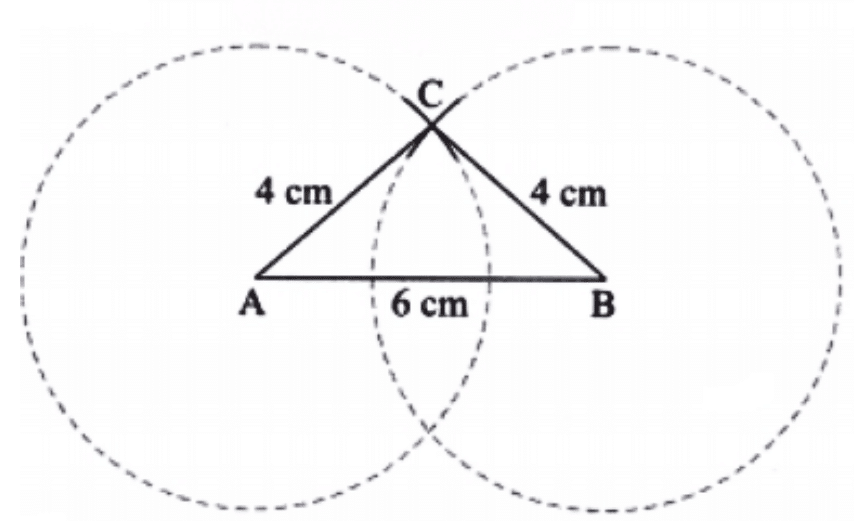
(b) Steps of Construction:
Step 1: Construct the base AB with one of the side lengths.
Let us choose AB = 3 cm.
Step 2: From A, construct a sufficiently long arc of radius 4 cm.
Step 3: From B, construct an arc of radius 5 cm such that it intersects the first arc.
Step 4: The point where both the arcs meet is the required third vertex C.
Join AC and BC to get ∆ABC.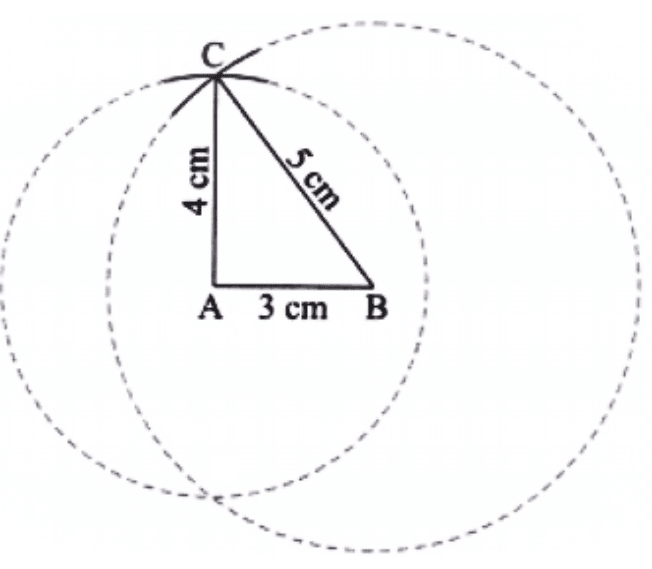
(c) Steps of Construction.
Do it yourself.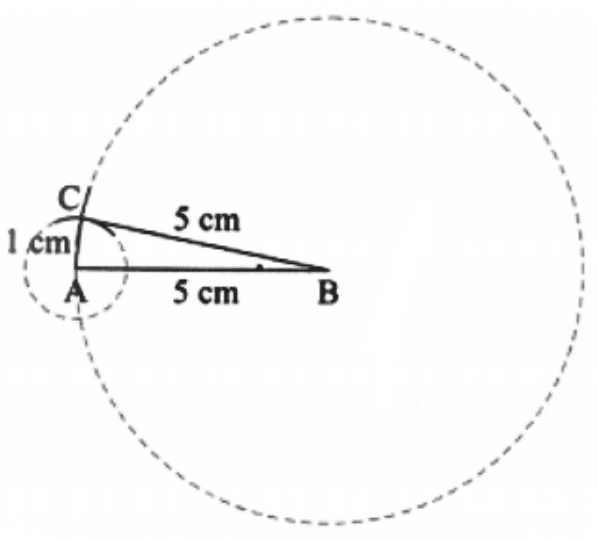
(d) Steps of Construction.
Do it yourself.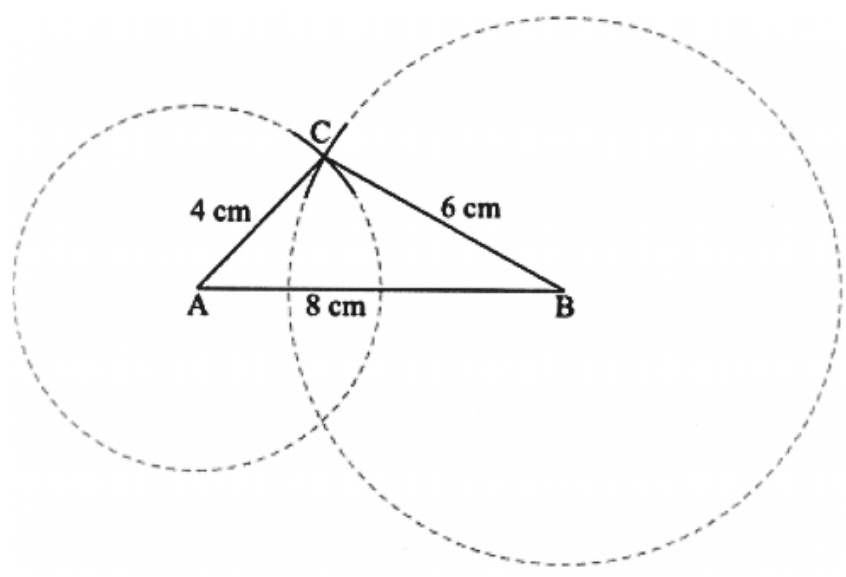
(e) Steps of Construction:
Step 1: Construct the base AB with a side length of 3.5 cm.
Step 2: From A, construct a long arc of radius 3.5 cm.
Step 3: Construct another arc of radius 3.5 cm from B.
Step 4: The point where both the arcs meet is the required third vertex C.
Join AC and BC to get ∆ABC.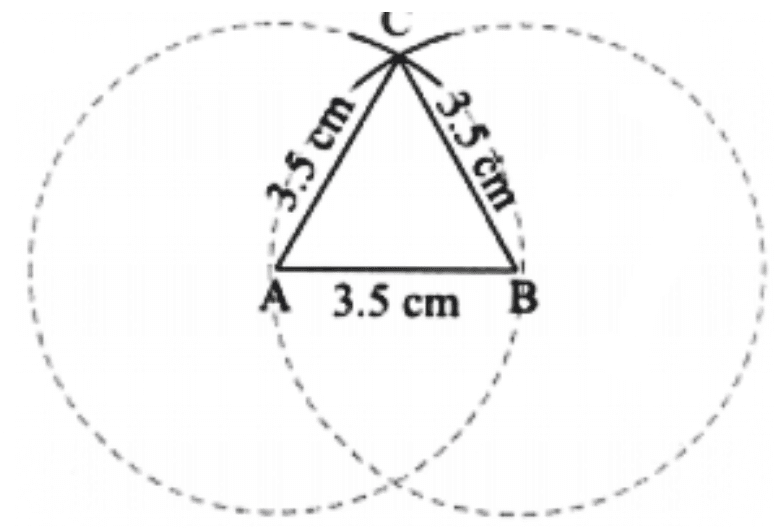
Figure it Out
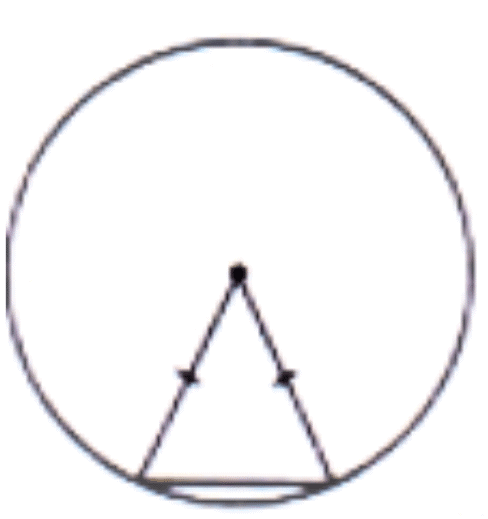
Q1: Use the points on the circle and/or the centre to form isosceles triangles.
Ans: Select any two points on the circle and connect them to the centre of the circle.
Also, join these points to each other. This will form an isosceles triangle as the two radii are equal in length.
 Q2: Use the points on the circles and/or their centres to form isosceles and equilateral triangles. The circles are of the same size.
Q2: Use the points on the circles and/or their centres to form isosceles and equilateral triangles. The circles are of the same size.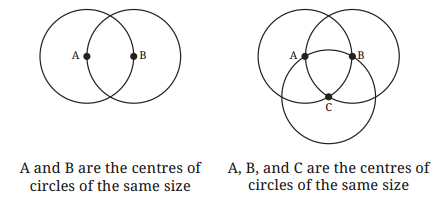
Ans: An isosceles triangle can be formed by connecting the intersecting points of two circles and the centres of either circle.
Here, isosceles triangles are AXY and BXY.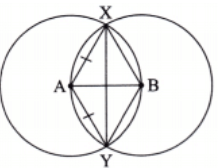
An equilateral triangle can be formed by connecting the centers of the 2 equal circles and one of their intersecting point.
Here, triangle AXB or triangle AYB is an equilateral triangle.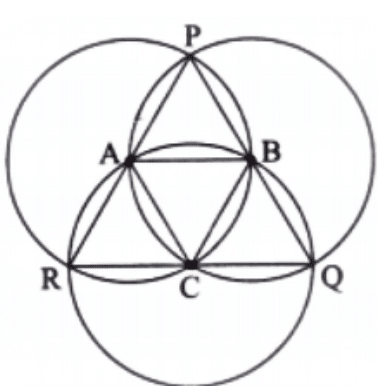
Page No. 151
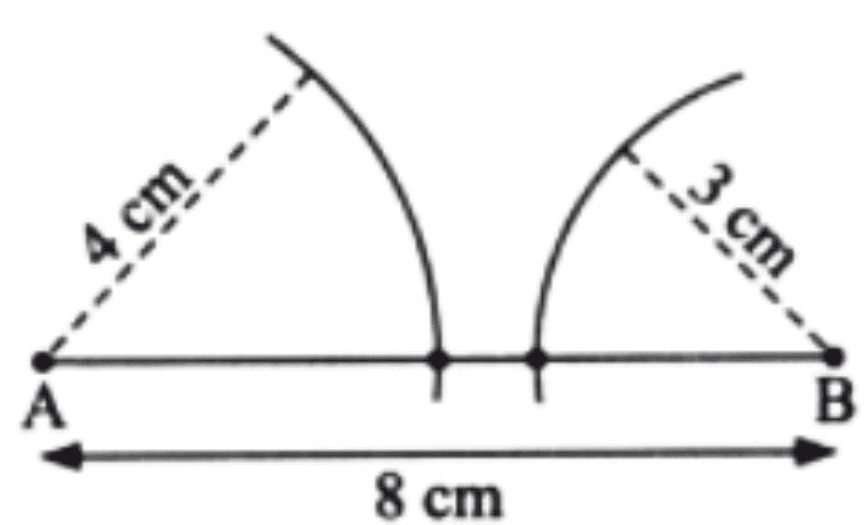
Q: Construct a triangle with sidelengths 3 cm, 4 cm, and 8 cm. What is happening? Are you able to construct the triangle?
Ans: Since the arcs from the points A and B do not meet. So, we are not able to construct the triangle with sidelengths 3 cm, 4 cm, and 8 cm.
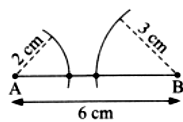
 Q: Here is another set of lengths: 2 cm, 3 cm, and 6 cm. Check if a triangle is possible for these sidelengths.
Q: Here is another set of lengths: 2 cm, 3 cm, and 6 cm. Check if a triangle is possible for these sidelengths.
Ans: Check triangle inequality: 2 + 3 < 6. The arcs of 2 cm from A and 6 cm from B (base AB = 3 cm) do not intersect, so no triangle is possible.
 Q: Try to find more sets of lengths for which a triangle construction is impossible. See if you can find any pattern in them.
Q: Try to find more sets of lengths for which a triangle construction is impossible. See if you can find any pattern in them.
Ans:
Examples:
- 1 cm, 2 cm, 4 cm (1 + 2 = 3 < 4).
- 5 cm, 5 cm, 11 cm (5 + 5 = 10 < 11).
- 2 cm, 3 cm, 7 cm (2 + 3 = 5 < 7).
Pattern: A triangle is impossible if the sum of the two smaller sides is less than or equal to the largest side.
Q: Can this understanding be used to tell something about the existence of a triangle having sidelengths 10 cm, 15 cm, and 30 cm?
Ans: Check triangle inequality: 10 + 15 = 25 < 30. The direct path CA = 30 cm is longer than the roundabout path CB + BA = 25 cm, violating the triangle inequality, so no triangle exists.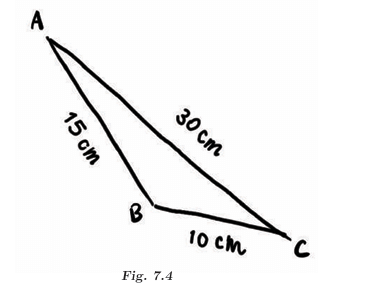
Page No. 153
Q: Can we say anything about the existence of a triangle having sidelengths 3 cm, 3 cm, and 7 cm? Verify your answer by construction.
Ans: Here, let us choose the direct path length AB = 7 cm.
And, the round about path length = BC + CA = 3 cm + 3 cm = 6 cm.
Since the direct path between two vertices is longer than the roundabout path via the third vertex. So, this triangle is not possible.
Also, by construction existence of a triangle having side lengths 3 cm, 3 cm, and 7 cm is not possible because if we draw arcs from point A and B then they do not meet.
Q: In the rough diagram in Fig. 7.4, is it possible to assign lengths in a different order such that the direct paths are always shorter than the roundabout paths? If this is possible, then a triangle might exist.
Ans: No, for 10 cm, 15 cm, and 30 cm, rearranging doesn’t help. The largest side (30) will always be greater than the sum of the other two (10 + 15 = 25), so a triangle cannot exist.
Q3: Is such rearrangement of lengths possible in the triangle?
Ans: No, the lengths 10 cm, 15 cm, and 30 cm cannot be rearranged to form a triangle because 10 + 15 = 25 is less than 30 in any order.
Page No. 154
Figure it Out
Q1: We checked by construction that there are no triangles having sidelengths 3 cm, 4 cm, and 8 cm; and 2 cm, 3 cm, and 6 cm. Check if you could have found this without trying to construct the triangle.
Ans: (a) Consider AB = 4 cm, BC = 3 cm and AC = 8 cm.
Now, direct path length = BC = 3 cm
And, roundabout path length = BA + AC
= 4 cm + 8 cm
= 12 cm
The direct path length is shorter than the roundabout path length.
Also, direct path length = AB = 4 cm
Roundabout path length = AC + BC
= 8 cm + 3 cm
= 11 cm
The direct path length is shorter than the roundabout path length.
Again, direct path length = AC = 8 cm
Then, roundabout path length = AB + BC
= 4 cm + 3 cm
= 7 cm
In this case, the direct path is longer than the roundabout path.
So, a triangle cannot exist.
(b) Consider AB = 3 cm, BC = 2 cm, AC = 6 cm
If we take the direct path = AC = 6 cm.
And, roundabout path length = AB + BC
= 3 cm + 2 cm
= 5 cm
Since the direct path is longer than the roundabout path. So, a triangle cannot exist.
Q2: Can we say anything about the existence of a triangle for each of the following sets of lengths?
(a) 10 km, 10 km, 25 km
(b) 5 mm, 10 mm, 20 mm
(c) 12 cm, 20 cm, 40 cm
You would have realised that using a rough figure and comparing the direct path lengths with their corresponding roundabout path lengths is the same as comparing each length with the sum of the other two lengths. There are three such comparisons to be made.
Ans:
(a) When we take the direct path = 25 km.
Then the roundabout path = 10 km + 10 km = 20 km.
Since the direct path is longer than the roundabout path.
So, the existence of a triangle is not possible.
(b) When we take the direct path = 20 mm.
Then the roundabout path = 10 mm + 5 mm = 15 mm.
Since the direct path is longer than the roundabout path.
So, the existence of a triangle is not possible.
(c) When we take the direct path = 40 cm.
Then the roundabout path = 12 cm + 20 cm = 32 cm.
Since the direct path is longer than the roundabout path.
So, the existence of a triangle is not possible.
Q3: For each set of lengths seen so far, you might have noticed that in at least two of the comparisons, the direct length was less than the sum of the other two (if not, check again!). For example, for the set of lengths 10 cm, 15 cm and 30 cm, there are two comparisons where this happens:
10 < 15 + 30
15 < 10 + 30
But this doesn’t happen for the third length: 30 > 10 + 15.
Ans: Yes, this will always happen. When you take any three lengths and arrange them in increasing order (a, b, c where a ≤ b ≤ c), the two smaller lengths (a and b) will always satisfy the comparisons:
- a < b + c (because a is the smallest, and b + c is larger).
- b < a + c (because b is less than c, so a + c is larger).
The third comparison (c < a + b) may or may not be true. Let’s check with examples:
For 3 cm, 4 cm, 5 cm:
- 3 < 4 + 5 (3 < 9, true).
- 4 < 3 + 5 (4 < 8, true).
- 5 < 3 + 4 (5 < 7, true).
All three are true.
For 2 cm, 3 cm, 6 cm:
- 2 < 3 + 6 (2 < 9, true).
- 3 < 2 + 6 (3 < 8, true).
- 6 < 2 + 3 (6 < 5, false).
Two comparisons are true.
So, in any set of three lengths, at least two comparisons will always hold because the two smaller lengths are naturally less than the sum of the other two.
Q: Will this always happen? That is, for any set of lengths, will there be at least two comparisons where the direct length is less than the sum of the other two? Explore for different sets of lengths.
Ans: Yes, in any set of three lengths, if you arrange them in increasing order (a, b, c), the two smaller lengths (a and b) will always have:
- a < b + c (true because a is the smallest).
- b < a + c (true because b is less than c).
So, at least two comparisons will hold. For example:
- 3, 4, 5: 3 < 4 + 5, 4 < 3 + 5, 5 < 3 + 4 (all true).
- 3, 4, 8: 3 < 4 + 8, 4 < 3 + 8, but 8 > 3 + 4 (only two hold).
Q: Further, for a given set of lengths, is it possible to identify which lengths will immediately be less than the sum of the other two, without calculations?
[Hint: Consider the direct lengths in the increasing order.]
Ans: Yes, arrange the lengths in increasing order: a, b, c (a ≤ b ≤ c). The two smaller lengths (a and b) will always be less than the sum of the other two:
- a < b + c (a is the smallest).
- b < a + c (b is less than c).
So, a and b will immediately satisfy the triangle inequality without calculations.
Q: Given three sidelengths, what do we need to compare to check for the existence of a triangle?
Ans: Compare each length with the sum of the other two:
- a < b + c
- b < a + c
- c < a + b
If all three conditions are true, a triangle exists. This is called the triangle inequality.
Page 156
Figure it Out
Q1: Which of the following lengths can be the sidelengths of a triangle? Explain your answers. Note that for each set, the three lengths have the same unit of measure.
(a) 2, 2, 5
(b) 3, 4, 6
(c) 2, 4, 8
(d) 5, 5, 8
(e) 10, 20, 25
(f) 10, 20, 35
(g) 24, 26, 28
We observe from the previous problems that whenever there is a set of lengths satisfying the triangle inequality (each length < sum of the other two lengths), there is a triangle with those three lengths as sidelengths.
Ans: A set of lengths can be the sidelengths of a triangle if each length < the sum of the other two lengths.
(a) 2 < 5 + 2 but 5 > 2 + 2
So, 2, 2, 5 cannot be the sidelengths of a triangle.
(b) 3 < 4 + 6, 4 < 3 + 6, 6 < 4 + 3
So, 3, 4, 6 can be the sidelengths of a triangle.
(c) 2 < 4 + 8, 4 < 2 + 8, but 8 > 4 + 2
So, 2, 4, 8 cannot be the sidelengths of a triangle.
(d) 5 < 5 + 8, 8 < 5 + 5
So, 5, 5, 8 can be the sidelengths of a triangle.
(e) 10 < 20 + 25, 20 < 25 + 10, 25 < 10 + 20
So, 10, 20, 25 can be the sidelengths of a triangle.
(f) 10 < 20 + 35, 20 < 10 + 35, but 35 > 10 + 20
So, 10, 20, 35 cannot be the sidelengths of a triangle.
(g) 24 < 26 + 28, 26 < 24 + 28, 28 < 24 + 26
So, 24, 26, 28 can be the sidelengths of a triangle.
Q: Will triangles always exist when a set of lengths satisfies the triangle inequality? How can we be sure?
Ans: Yes, if the lengths satisfy the triangle inequality (each length is less than the sum of the other two), a triangle always exists. We can be sure because when we construct the triangle by drawing the longest side as the base and arcs for the other two sides, the arcs will intersect (since the sum of the two smaller lengths is greater than the longest length), forming the triangle.
Page No. 159
Q: How will the two circles turn out for a set of lengths that do not satisfy the triangle inequality? Find 3 examples of sets of lengths for which the circles:
(a) touch each other at a point,
(b) do not intersect.
Ans:
(a) Circles touch: Sum of two smaller lengths = longest length.
Examples:
- 2, 2, 4 (2 + 2 = 4).
- 3, 3, 6 (3 + 3 = 6).
- 5, 5, 10 (5 + 5 = 10).
(b) Circles do not intersect: Sum of two smaller lengths < longest length.
Examples:
- 2, 3, 6 (2 + 3 < 6).
- 1, 2, 4 (1 + 2 < 4).
- 5, 5, 11 (5 + 5 < 11).
Q: Frame a complete procedure that can be used to check the existence of a triangle.
Ans:
- Take the three lengths and arrange them in increasing order: a, b, c (a ≤ b ≤ c).
- Check if the sum of the two smaller lengths is greater than the longest length: a + b > c.
- If yes, a triangle exists. If no, a triangle does not exist.
Figure it Out
Q1: Check if a triangle exists for each of the following set of lengths:
(a) 1, 100, 100;
(b) 3, 6, 9;
(c) 1, 1, 5;
(d) 5, 10, 12.
Ans: We know that when each length is smaller than the sum of the other two, we say that the lengths satisfy the triangle inequality, and when a set of lengths satisfies the triangle inequality, then a triangle exists.
(a) Here 1 < 100 + 100, 100 < 100 + 1
So, for sidelengths 1, 100, 100, a triangle exists.
(b) 3 < 6 + 9, 6 < 3 + 9, but 9 = 6 + 3
So, for sidelengths 3, 6, 9, a triangle does not exist.
(c) 1 < 1 + 5, but 5 > 1 + 1
So, for sidelengths 1, 1, 5, a triangle does not exist.
(d) 5 < 10 + 12, 10 < 5 + 12, 12 < 10 + 5
So, for sidelengths 5, 10, and 12, a triangle exists.
Q2: Does there exist an equilateral triangle with sides 50, 50, 50? In general, does there exist an equilateral triangle of any sidelength? Justify your answer.
Ans: Yes, an equilateral triangle with sides 50, 50, 50 exists because 50 + 50 = 100 > 50, satisfying the triangle inequality.
In general, for any length a, an equilateral triangle with sides a, a, a exists because a + a = 2a > a, always satisfying the triangle inequality.
Q3: For each of the following, give at least 5 possible values for the third length so there exists a triangle having these as sidelengths (decimal values could also be chosen):
(a) 1, 100
(b) 5, 5
(c) 3, 7
Ans: (a) 5 possible values for the third length would be 99.5, 99.8, 100, 100.5, 100.9
Since, 100 < 1 + 99.5, 100 < 1 + 99.8, 100 < 1 + 100, 100 < 1 + 100.5, and 100 < 1 + 100.9
(b) 5 possible values for the third length would be 1, 3.5, 5, 7.5, 8.9
Since, 5 < 1 + 5, 5 < 5 + 3.5, 5 < 5 + 5, 5 < 5 + 7.5, and 5 < 5 + 8.9
(c) 5 possible values for the third length would be 4.5, 5, 6.9, 8, 9.8
Since, 7 < 3 + 4.5, 7 < 5 + 3, 7 < 3 + 6.9, 7 < 3 + 8, 7 < 3 + 9.8
Page No. 160
Q: See if you can describe all possible lengths of the third side in each case, so that a triangle exists with those side lengths.
For example, in case (a), all numbers strictly between 99 and 101 would be possible.
Ans: When two sides are given, then the third side must lie between the sum and the difference of the two lengths for the existence of a triangle.
Therefore, (b) numbers will lie between 0 and 10, and (c) numbers will be between 4 and 10.
Page No. 161
Figure it Out
Q1: Construct triangles for the following measurements where the angle is included between the sides:
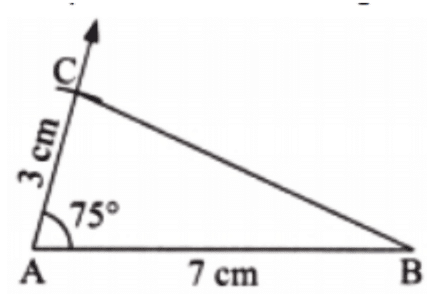
(a) 3 cm, 75°, 7 cm;
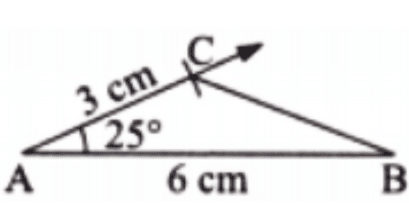
(b) 6 cm, 25°, 3 cm;
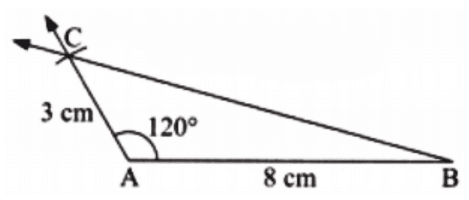
(c) 3 cm, 120°, 8 cm.
Ans:
(a) Step 1: Construct a side AB of length 7 cm.
Step 2: Construct ∠A = 75° by drawing the other arm of the angle.
Step 3: Mark the point C on the other arm such that AC = 3 cm.
Step 4: Join BC to get the required triangle.
 (b) Step 1: Construct a side AB of length 6 cm.
(b) Step 1: Construct a side AB of length 6 cm.
Step 2: Construct ∠A = 25° by drawing the other arm of the angle.
Step 3: Mark the point C on the other arm such that AC = 3 cm.
Step 4: Join BC to get the required triangle.
 (c) Step 1: Construct a side AB of length 8 cm.
(c) Step 1: Construct a side AB of length 8 cm.
Step 2: Construct ∠A = 120° by drawing the other arm of the angle.
Step 3: Mark the point C on the other arm such that AC = 3 cm.
Step 4: Join BC to get the required triangle.
Q2: We have seen that triangles do not exist for all sets of sidelengths. Is there a combination of measurements in the case of two sides and the included angle where a triangle is not possible? Justify your answer using what you observe during construction.
Ans: A triangle is always possible when given two sides and the included angle. During construction, draw the base (first side), make the given angle at one end, and draw a ray. Then, from the other end of the base, draw an arc of the second side’s length. The arc will always intersect the ray at a point (the third vertex), forming a triangle. This works for any angle and side lengths, so a triangle is always possible.
Page 162
Figure it Out
Q1: Construct triangles for the following measurements:
(a) 75°, 5 cm, 75°
Ans: Step 1: Draw base AB = 5 cm.
Step 2: At point A, use a protractor to draw a ray at 75°.
Step 3: At point B, draw a ray at 75°.
Step 4: The rays intersect at point C. Join AC and BC to form triangle ABC.
(b) 25°, 3 cm, 60°
Ans: Step 1: Draw base AB = 3 cm.
Step 2: At point A, use a protractor to draw a ray at 25°.
Step 3: At point B, draw a ray at 60°.
Step 4: The rays intersect at point C. Join AC and BC to form triangle ABC.
(c) 120°, 6 cm, 30°
Ans: Step 1: Draw base AB = 6 cm.
Step 2: At point A, use a protractor to draw a ray at 120°.
Step 3: At point B, draw a ray at 30°.
Step 4: The rays intersect at point C. Join AC and BC to form triangle ABC.
Q: Do triangles always exist?
Ans: No, triangles do not always exist for every combination of two angles and their included side. If the sum of the two angles is 180° or more, the rays drawn from the ends of the base will not meet, so no triangle forms. For example:
- For 90°, 5 cm, 90°: Sum = 90° + 90° = 180°. The rays are parallel and don’t intersect, so no triangle exists.
- For 120°, 5 cm, 70°: Sum = 120° + 70° = 190° > 180°. The rays diverge and don’t intersect, so no triangle exists.
In the given cases:
(a) 75° + 75° = 150° < 180°, so a triangle exists.
(b) 25° + 60° = 85° < 180°, so a triangle exists.
(c) 120° + 30° = 150° < 180°, so a triangle exists.
A triangle exists only if the sum of the two angles is less than 180°.
Q: Do triangles exist for every combination of two angles and their included side? Explore.
Ans: No, triangles do not exist for every combination. If the sum of the two angles is 180° or more, the rays drawn from the ends of the base will not meet, so no triangle forms. For example, 90° and 90° (sum = 180°) makes the rays parallel, so they don’t intersect.
Q: Find examples of measurements of two angles with the included side where a triangle is not possible.
Ans: Examples:
- 90°, 90°, 5 cm (sum = 180°, rays are parallel).
- 100°, 80°, 5 cm (sum = 180°, rays are parallel).
- 120°, 70°, 5 cm (sum = 190°, rays diverge).
In each case, the rays don’t meet, so no triangle forms.
Page No. 163
Figure it Out
1. For each of the following angles, find another angle for which a triangle is (a) possible, (b) not possible. Find at least two different angles for each category:
(a) 30°
Ans:
- Possible: 60° (30° + 60° = 90° < 180°), 120° (30° + 120° = 150° < 180°).
- Not possible: 150° (30° + 150° = 180°), 160° (30° + 160° = 190° > 180°).
(b) 70°
Ans:
- Possible: 50° (70° + 50° = 120° < 180°), 100° (70° + 100° = 170° < 180°).
- Not possible: 110° (70° + 110° = 180°), 120° (70° + 120° = 190° > 180°).
(c) 54°
- Possible: 60° (54° + 60° = 114° < 180°), 90° (54° + 90° = 144° < 180°).
- Not possible: 126° (54° + 126° = 180°), 130° (54° + 130° = 184° > 180°).
(d) 144°
- Possible: 10° (144° + 10° = 154° < 180°), 20° (144° + 20° = 164° < 180°).
- Not possible: 36° (144° + 36° = 180°), 40° (144° + 40° = 184° > 180°).
Q2: Determine which of the following pairs can be the angles of a triangle and which cannot:
(a) 35°, 150°
Ans: 35 + 150 = 185° > 180°. Not possible.
(b) 70°, 30°
Ans: 70 + 30 = 100° < 180°. Possible.
(c) 90°, 85°
Ans: 90 + 85 = 175° < 180°. Possible.
(d) 50°, 150°
Ans: 50 + 150 = 200° > 180°. Not possible.
Q: Like the triangle inequality, can you form a rule that describes the two angles for which a triangle is possible? Can the sum of the two angles be used for framing this rule?
Ans: Yes, the rule is: A triangle is possible if the sum of the two angles is less than 180°. If the sum is 180° or more, no triangle is possible. The sum of the two angles can be used to frame this rule.
Page No. 164
Q: What could the measure of the third angle be? Does this measure change if the base length is changed to some other value, say 7 cm? Construct and find out.
Ans: For angles 60° and 70°:
Third angle = 180° - (60° + 70°) = 180° - 130° = 50°.
Construct with base 5 cm, then with 7 cm. In both cases, the third angle remains 50°, so the base length does not change the third angle.
Q: Try experimenting with different triangles to see if there is a relation between any two angles and the third one. To find this relation, what data will you keep track of and how will you organise the data you collect?
Ans: Do it Yourself!
Page No. 165
Figure it Out
Q1: Find the third angle of a triangle (using a parallel line) when two of the angles are:
(a) 36°, 72°
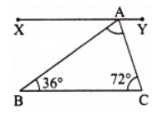
Ans: (a) Here ∠B = 36° and ∠C = 72°.
Since the line BC is parallel to XY.
So, ∠XAB = ∠B = 36° [Alternate angles] ….. (i)
and ∠YAC = ∠C = 72° [Alternate angles] …… (ii)
Also, ∠XAB + ∠BAC + ∠YAC = 180° [∵∠XAY is a straight angle]
⇒ 36° + ∠BAC + 72° = 180° [Using (i) and (ii)]
⇒ ∠BAC = 180°- 108° = 72°.
(b) 150°, 15°
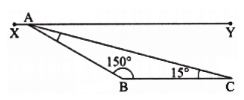
Ans: Here ∠B = 150° and ∠C = 15°.
Since the line BC is parallel to XY.
So, ∠XAB = ∠B = 150° [Alternate angles] ….. (i)
and ∠YAC = ∠C = 15° [Alternate angles] …… (ii)
Also, ∠XAB + ∠BAC + ∠YAC = 180° [∠XAY is a straight angle]
⇒ 150° + ∠BAC + 15° = 180° [Using (i) and (ii)]
⇒ ∠BAC = 180° – 165° = 15°
(c) 90°, 30°
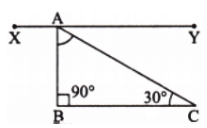
Ans: Here ∠B = 90° and ∠C = 30°.
Since the line BC is parallel to XY.
So, ∠XAB = ∠B = 90° [Alternate angles] …… (i)
and ∠YAC = ∠C = 30° [Alternate angles] …… (ii)
Also, ∠XAB + ∠BAC + ∠YAC = 180° [∠XAY is a straight angle]
⇒ 90° + ∠BAC + 30° = 180° [Using (i) and (ii)]
⇒ ∠BAC = 180°- 120° = 60°
(d) 75°, 45°
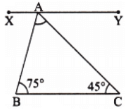
Ans: Here ∠B = 75° and ∠C = 45°.
Since the line BC is parallel to XY.
So, ∠XAB = ∠B = 75° [Alternate angles] ….. (i)
and ∠YAC = ∠C = 45° [Alternate angles] ….. (ii)
Also, ∠XAB + ∠BAC + ∠YAC = 180° [∠XAY is a straight angle]
⇒ 75° + ∠BAC + 45° = 180° [Using (i) and (ii)]
⇒ ∠BAC = 180° – 120° = 60°
 Q2: Can you construct a triangle all of whose angles are equal to 70°? If two of the angles are 70°, what would the third angle be? If all the angles in a triangle have to be equal, then what must its measure be? Explore and find out.
Q2: Can you construct a triangle all of whose angles are equal to 70°? If two of the angles are 70°, what would the third angle be? If all the angles in a triangle have to be equal, then what must its measure be? Explore and find out.
Ans: No, it is not possible to construct a triangle with all angles equal to 70°.
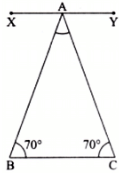
If we take two base angles as 70° that is, ∠B and ∠C = 70°, then we have to find ∠BAC.
Since XY is parallel to BC.
So, ∠XAB = ∠B = 70° ….. (i)
and ∠YAC = ∠C = 70° …… (ii)
Also, ∠XAB + ∠BAC + ∠YAC = 180°
⇒ 70° + ∠BAC + 70° = 180° [Using (i) and (ii)]
⇒ ∠BAC = 180° – 140° = 40°.
So, the third angle would be 40°.
If all the angles in a triangle have to be equal, then each angle must measure 60°. This type of triangle is called an equilateral triangle.
Q3: Here is a triangle in which we know ∠B = ∠C and ∠A = 50°. Can you find ∠B and ∠C?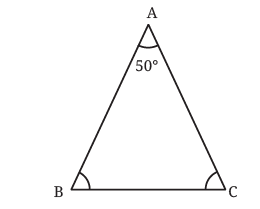 Ans: Given ∠A = 50° and ∠B = ∠C.
Ans: Given ∠A = 50° and ∠B = ∠C.
Draw a line XY that is parallel to BC.
Now, ∠XAB = ∠B and ∠YAC = ∠C [Alternate angles] …… (i)
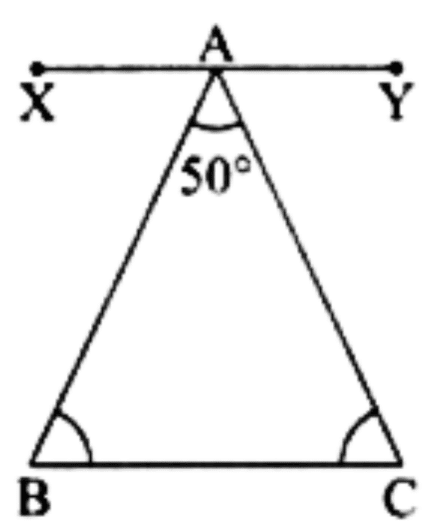
Also, ∠XAB + ∠BAC + ∠YAC = 180°
⇒ ∠B + 50° + ∠C = 180° [Using (i)]
∠B + ∠C = 180° – 50° = 130°
⇒ 2∠B = 130°
⇒ ∠B = 65° = ∠C
Page No. 167
Exterior Angles
The angle formed between the extension of a side of a triangle and the other side is called an exterior angle of the triangle. In this figure, ∠ACD is an exterior angle.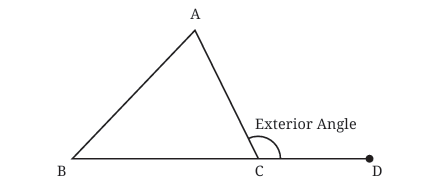
Q: Find ∠ACD, if ∠A = 50°, and ∠B = 60°.
Ans: ∠ACB = 180° - (50 + 60) = 70°.
∠ACD = 180° - ∠ACB = 110° (straight angle).
Q: Find the exterior angle for different measures of ∠A and ∠B. Do you see any relation between the exterior angle and these two angles?
[Hint: From angle sum property, we have ∠A + ∠B + ∠ACB = 180°.] We also have ∠ACD + ∠ACB = 180°, since they form a straight angle. What does this show?
Ans: The exterior angle (e.g., ∠ACD) is equal to the sum of the two non-adjacent angles (∠A + ∠B).
Example: If ∠A = 50°, ∠B = 60°:
∠ACB = 180° - (50° + 60°) = 70°.
∠ACD = 180° - 70° = 110°.
Also, ∠A + ∠B = 50° + 60° = 110°, which matches ∠ACD.
This relation holds for any triangle: Exterior angle = sum of the two opposite angles.
Page No. 168
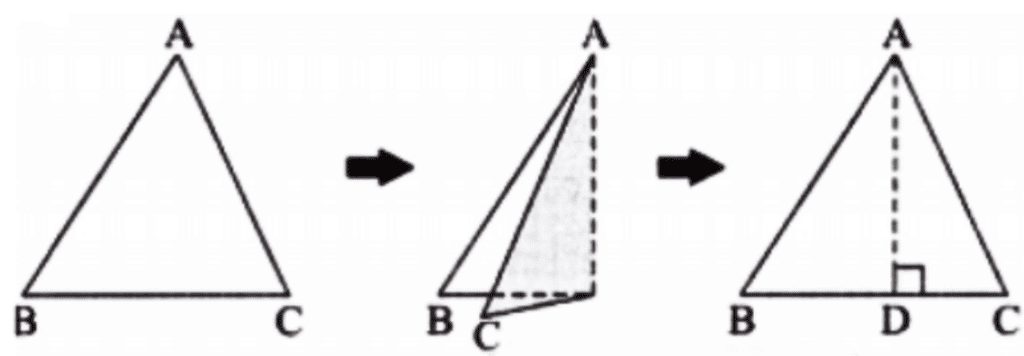
Q: Cut out a paper triangle. Fix one of the sides as the base. Fold it in such a way that the resulting crease is an altitude from the top vertex to the base. Justify why the crease formed should be perpendicular to the base.
Ans: The perpendicularity happens because the shortest distance between a point, i.e., a vertex, and a line, i.e., the base is always a perpendicular line.
By folding the paper, we construct the shortest distance, ensuring the crease is perpendicular to the base.
Q: What could an acute-angled triangle be? Can we define it as a triangle with one acute angle? Why not?
Ans: An acute-angled triangle is a triangle in which all three angles are less than 90°.
We cannot define it as a triangle with only one acute angle, because every triangle must have at least two acute angles (since the sum of all angles in a triangle is always 180°).
If a triangle has:
One right angle → it is a right-angled triangle.
One obtuse angle → it is an obtuse-angled triangle.
So, just having one acute angle does not make a triangle acute-angled.
To be called acute-angled, all angles must be acute (less than 90°).
Figure it Out
Q1: Construct a triangle ABC with BC = 5 cm, AB = 6 cm, CA = 5 cm. Construct an altitude from A to BC.
Ans: Steps of Construction:
Step 1: Draw the base AB = 6 cm.
Step 2: Using a compass, construct a sufficiently long arc of radius 5 cm from A.
Step 3: Construct another arc of radius 5 cm from B such that it intersects the first arc.
Step 4: The point where both the arcs meet is the required third vertex C. Join AC and BC to get ∆ABC.
Step 5: Keep the ruler aligned to BC. Place the set square on the ruler such that one of the edges of the right angle touches the ruler.
Step 6: Slide the set square along the ruler till the perpendicular edge of the set square touches the vertex A.
Step 7: Draw the altitude through A to BC using the perpendicular edge of the set square.
Q2: Construct a triangle TRY with RY = 4 cm, TR = 7 cm, ∠R = 140°. Construct an altitude from T to RY.
Ans: Steps of Construction:
Step 1: Construct a side TR of length 7 cm.
Step 2: Construct ∠R = 140° by drawing the other arm of the angle.
Step 3: Mark the point Y on the other arm such that RY = 4 cm.
Step 4: Join TY to get the required triangle.
Step 5: Keep the ruler aligned to RY. Place the set square on the ruler such that one of the edges of the right angle touches the ruler.
Step 6: Slide the set square along the ruler till the perpendicular edge of the set square touches the vertex T.
Step 7: Extend the line YR and then draw the altitude through T on YR using the perpendicular edge of the set square.
Q3: Construct a right-angled triangle ABC with ∠B = 90°, AC = 5 cm. How many different triangles exist with these measurements?
[Hint: Note that the other measurements can take any values. Take AC as the base. What values can ∠A and ∠C take so that the other angle is 90°?]
Ans:
Given, ∠B = 90°, and AC = 5 cm (hypotenuse)
Since ∠B = 90°, ∠A and ∠C add upto 90°.
If we fixed AC = 5 cm and ∠A and ∠C vary, then there are infinitely many triangles possible.
Because the shape of the triangle can change with the different values of angles A and C.
One such example is given here:
Q4: Through construction, explore if it is possible to construct an equilateral triangle that is (i) right-angled (ii) obtuse-angled. Also construct an isosceles triangle that is (i) right-angled (ii) obtuse-angled.
Ans:
An equilateral triangle that is right-angled and obtuse-angled is not possible because each angle of an equilateral triangle is always 60°.
An isosceles right-angled triangle has one angle of 90° and the other two angles of 45° each.
An isosceles obtuse-angled triangle can have one angle as 120° and the other two angles of 30° each.
Page No. 172
Q: There is a spider in a corner of a box. It wants to reach the farthest opposite corner (marked in the figure). Since it cannot fly, it can reach the opposite point only by walking on the surfaces of the box. What is the shortest path it can take?  Take a cardboard box and mark the path that you think is the shortest from one corner to its opposite corner. Compare the length of this path with that of the paths made by your friends.
Take a cardboard box and mark the path that you think is the shortest from one corner to its opposite corner. Compare the length of this path with that of the paths made by your friends.
Hint: Ans:
Ans:
Imagine unfolding the box into a flat shape (like opening up a cardboard box).
Now, the path becomes a straight line on this flat surface!
This helps the spider take the shortest route, just like a straight line is the shortest distance between two points.
The image in the hint shows how the box can be opened to make it flat. The spider’s path is then shown as a red straight line.
So, By unfolding the box and drawing a straight line, you get the shortest path from one corner to the opposite corner on the surfaces.
|
41 videos|251 docs|8 tests
|
FAQs on NCERT Solutions for Class 7 Maths Chapter 7 A Tale of Three Intersecting Lines
| 1. What are the main concepts covered in "A Tale of Three Intersecting Lines"? |  |
| 2. How can I identify parallel and intersecting lines in a given diagram? |  |
| 3. What are the angle relationships that occur when intersecting lines meet? |  |
| 4. How can I apply the concepts of intersecting lines to solve mathematical problems? |  |
| 5. Are there any real-life applications of intersecting lines and angles? |  |





















