Motion in one Dimension Chapter Notes | Technical Science for Grade 10 PDF Download
| Table of contents |

|
| Origin, Position, Distance, and Displacement |

|
| Speed and Velocity |

|
| Acceleration |

|
| Points to Remember |

|
| Difficult Words |

|
| Summary |

|
Origin, Position, Distance, and Displacement
This section explains how to describe where an object is and how far it moves, using position, reference points, origin, distance, and displacement.
Motion in One Dimension
Definition: Motion in one dimension is movement along a straight line, either forward or backward.
Explanation: Motion means movement. This chapter focuses on objects moving in a straight line, like going left or right on a road.

Position and Reference Points
Definition: Position is where an object is located compared to a reference point.Reference Points: Known spots used to find an object’s location.
Examples:
- The zero mark on a ruler.
- The ground when measuring a high jump.
Importance: Reference points help you know exactly where something is, like saying a sign is “to the right of the school gate.”
Origin and Position
Origin: The starting point for measuring position on a graph, usually marked as zero (0).Position Description:
- Right of the origin is positive (+).
- Left of the origin is negative (-).
- Example: Point A at +5 cm is 5 cm right of the origin; Point B at -3 cm is 3 cm left.
Measurement: Positions are measured in units like centimetres or metres from the origin.
Distance
Definition: Distance is the total length of the path an object travels between two points.Features:
- Symbol: d
- Unit: Metre (m)
- Type: Scalar (only size, no direction).
Example: In a 400 m race, the distance is 400 m, no matter which way the runner goes.
Measurement: Distance follows the actual path, like a curvy road.
Displacement
Definition: Displacement is the shortest straight-line distance between two points, including the direction.Features:
- Symbol: d
- Unit: Metre (m)
- Type: Vector (has size and direction).
Describing Direction:
- Positive (+) or negative (-).
- Up, down, north, south, east, west.
- Compass directions (e.g., north-east).
- Bearings (degrees clockwise from north, e.g., 45°).
Example: Thabo walks 2 km along a winding road (distance), but the straight-line distance from start to end is 1 km north-east (displacement).
Difference Between Distance and Displacement
- Distance: Total path length, no direction (scalar).
Example: Thabo’s 2 km walk on a winding road. - Displacement: Shortest path with direction (vector).
- Example: Thabo’s 1 km north-east displacement.
Use: Displacement shows where an object ends up compared to its start; distance shows how far it traveled.
Speed and Velocity
This section covers speed and velocity, which describe how fast an object moves, and explains the difference between scalar and vector quantities.
 The 200 m track
The 200 m track
Speed
Definition: Speed is how fast an object covers distance.Formula:
speed = distance / time or speed = d / t
- d: Distance (metres, m)
- t: Time (seconds, s)
- Speed: Metres per second (m/s)
Features:
- Type: Scalar (size only, no direction).
- Example: Usain Bolt runs 200 m in 19.19 s, speed = 200 / 19.19 = 10.42 m/s.
Average Speed: Speed usually means average speed, as it changes during motion (e.g., Bolt starts slow, then runs faster).
Velocity
Definition: Velocity is how fast an object’s displacement changes.Formula:
v = d / t
- v: Velocity (metres per second, m/s)
- d: Displacement (metres, m)
- t: Time (seconds, s)
Features:
- Type: Vector (has size and direction).
- Example: A box moves 100 m right in 20 s, velocity = 100 / 20 = 5 m/s to the right.
Importance: Velocity tells both how fast and in which direction an object moves, unlike speed.
Difference Between Speed and Velocity
- Speed: Based on distance (scalar), ignores direction.
Example: Karabo jogs 5 km in 30 min, speed = 10 km/h. - Velocity: Based on displacement (vector), includes direction.
- Example: Karabo’s velocity is 10 km/h east if she jogs east.
Use: Velocity matters when direction is important, like finding Karabo after her jog.
Vector Diagrams for Displacement and Velocity
Purpose: To find total displacement or velocity when an object moves in multiple steps along a straight line.Method:
- Draw vectors as arrows (length shows size, arrowhead shows direction).
- Connect vectors tail-to-head to find the resultant.
- Example: A box moves 3 m right, then 18 m left. Resultant displacement = 15 m left, velocity = 15 / 30 = 0.5 m/s to the left over 30 s.
Acceleration
This section explains acceleration, how velocity changes over time, and how ticker-timers measure motion.
Acceleration
Definition: Acceleration is how quickly velocity changes.Formula:
a = (final velocity - initial velocity) / time
or
a = (vf - vi) / t
- a: Acceleration (metres per second per second, m/s²)
- vf: Final velocity (m/s)
- vi: Initial velocity (m/s)
- t: Time (seconds, s)
Features:
- Type: Vector (has size and direction).
- Unit Explanation:
Acceleration = change in velocity (m/s) / time (s) = m/s/s = m/s²
Conditions:
- Acceleration happens when velocity changes (speeding up or slowing down).
- No acceleration if velocity stays the same, even if moving fast.
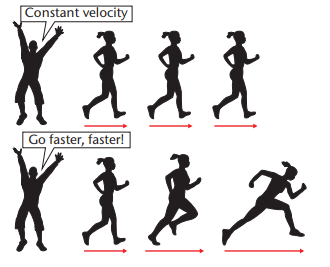 Constant velocity and changing velocity
Constant velocity and changing velocity
Positive and Negative Acceleration
- Direction: Acceleration is positive (+) or negative (-) depending on its direction compared to velocity.
- Same Sign: If acceleration and velocity have the same sign (e.g., both positive), the object speeds up.
Example: Velocity from 2 m/s to 12 m/s in 5 s, a = (12 - 2) / 5 = 2 m/s². - Opposite Sign: If signs are different, the object slows down.
Example: Velocity from 12 m/s to 2 m/s in 5 s, a = (2 - 12) / 5 = -2 m/s². - Negative Direction: For objects moving left (negative):
Velocity from -2 m/s to -12 m/s (speeding up), a = (-12 - (-2)) / 5 = -2 m/s².
Velocity from -12 m/s to -2 m/s (slowing down), a = (-2 - (-12)) / 5 = +2 m/s².
Terminology: Science uses “negative acceleration” instead of “deceleration” for slowing down.
Calculating with Conversions
Velocity Conversions:- From km/h to m/s: Multiply by 1000 / 3600 = 5 / 18.
Example: 30 km/h = 30 × 5 / 18 = 8.33 m/s. - From m/s to km/h: Multiply by 3600 / 1000 = 18 / 5.
Example: 13 m/s = 13 × 18 / 5 = 46.8 km/h.
Example: A motorcycle’s velocity changes from 30 km/h (8.33 m/s) to 90 km/h (25 m/s) in 10 s, a = (25 - 8.33) / 10 = 1.67 m/s².
Ticker-Timer for Measuring Velocity
Ticker-Timer: A device that makes dots on paper tape 50 times per second (each dot = 1 / 50 = 0.02 s).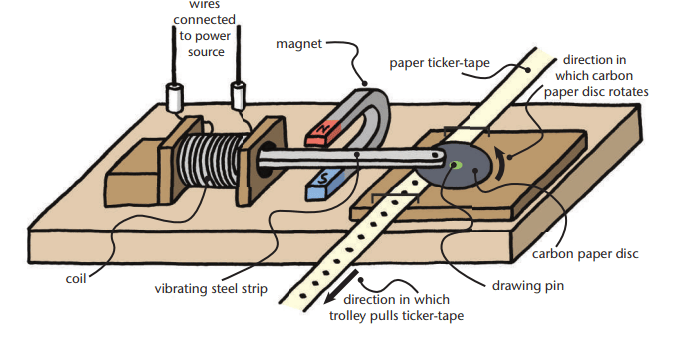 A ticker-timeTape Analysis:
A ticker-timeTape Analysis:
- Close Dots: Slow speed (dots close together).
- Far Dots: Fast speed (dots farther apart).
- Changing Dots: Dots getting farther apart mean speeding up; closer together mean slowing down.
Strips:
A strip with 10 spaces (11 dots) represents 10 / 50 = 0.2 s.
Velocity Formula:
v = d / t
- d: Strip length (cm)
- t: Time (s, e.g., 0.2 s for 10 spaces)
- Velocity: cm/s (not changed to m/s for ticker-tape).
Example: A 10 cm strip with 10 spaces, v = 10 / 0.2 = 50 cm/s.
Points to Remember
- Motion in one dimension is movement in a straight line, with position measured from a reference point or origin.
- Distance (scalar) is the total path traveled, while displacement (vector) is the shortest path with direction.
- Speed (scalar) measures how fast distance changes, while velocity (vector) measures displacement change, both in m/s.
- Acceleration (vector) is how velocity changes, measured in m/s², and can be positive (speeding up) or negative (slowing down).
- Ticker-timers measure velocity with 50 dots per second, where dot spacing shows speed or acceleration changes.
Difficult Words
- Motion: Moving from one place to another.
- One Dimensional: Movement only in a straight line, forward or backward.
- Position: Where an object is compared to a reference point.
- Reference Point: A known spot to describe an object’s location.
- Origin: The zero point on a graph for measuring position.
- Distance: Total path length traveled (scalar).
- Displacement: Shortest straight-line distance with direction (vector).
- Speed: How fast distance is covered (scalar, m/s).
- Velocity: How fast displacement changes, with direction (vector, m/s).
- Acceleration: How quickly velocity changes, with direction (vector, m/s²).
- Ticker-Timer: A device that marks dots on tape to measure motion.
Summary
This chapter covers motion in one dimension, meaning movement along a straight line. Position is where an object is relative to a reference point, often the origin (zero) on a graph, with positive or negative values showing direction. Distance, a scalar, is the total path length in metres, while displacement, a vector, is the shortest path with direction. Speed, a scalar, is how fast distance changes (speed = distance / time), usually calculated as average speed in m/s. Velocity, a vector, is how fast displacement changes (v = d / t), including direction. Acceleration, a vector, is how velocity changes (a = (final velocity - initial velocity) / time), measured in m/s², and can be positive (speeding up) or negative (slowing down) based on direction. Ticker-timers measure velocity by marking 50 dots per second, with dot spacing showing speed or acceleration changes. These ideas help analyze straight-line motion in science and engineering.
|
1 videos|77 docs|5 tests
|




















