Circles, Angles, and Angular Movement Chapter Notes | Mathematics for Grade 10 PDF Download
| Table of contents |

|
| Parts of a Circle |

|
| Understanding Pi (π) |

|
| Measuring Angles in Degrees |

|
| Radian Measure |

|
| Converting Between Degrees and Radians |

|
| Points to Remember |

|
| Difficult Words |

|
| Summary |

|
Parts of a Circle
This section defines the key components of a circle, essential for understanding subsequent calculations.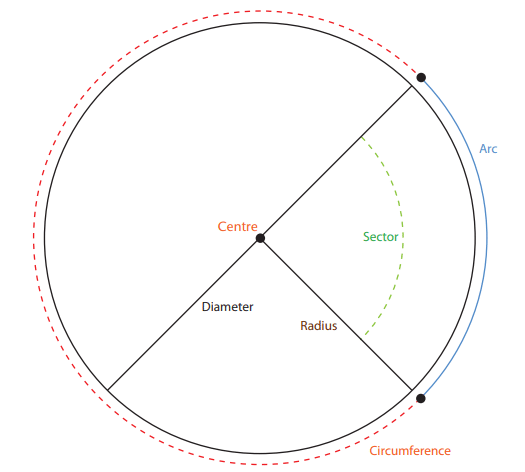
Circumference: The total length around the edge of a circle. It is calculated using the formulas:
C = 2πr (where r is the radius)
C = πd (where d is the diameter).Diameter: A straight line passing through the center of the circle, connecting two opposite points on the circumference. It is twice the length of the radius: d = 2r.
Radius: A line segment from the center of the circle to any point on the circumference.
Arc: A portion of the circumference of a circle.
Sector: A pie-shaped region of a circle enclosed by two radii and the arc between them.
Central Angle: An angle with its vertex at the center of the circle, formed by two radii.
Standard Position of an Angle: Angles are measured starting from the positive horizontal axis (right side) and moving counterclockwise, unless otherwise specified.
Understanding Pi (π)
This section explores the constant π, crucial for circle calculations.Definition of Pi:
- Pi (π) is the ratio of a circle’s circumference to its diameter: π = C/d.
- This ratio is constant for all circles, regardless of size, approximately equal to 3.14 or 22/7 as a fraction.
Key Formulas:
- Circumference: C = πd or C = 2πr.
- Diameter: d = 2r.
Properties:
- Pi is a constant, meaning its value does not change with the size of the circle.
- It is used in calculations involving circumferences, arc lengths, and areas of circles.
Measuring Angles in Degrees
This section revisits angle measurement in degrees and introduces subdivisions for precision.Degrees and Revolutions:
- A full revolution (complete circle) is 360°.
- One degree (1°) is 1/360 of a revolution.
Subdividing Degrees:
Decimal Notation: Angles can be expressed as decimals, e.g., 130.831°.
Minutes and Seconds:
- 1° = 60 minutes (60').
- 1 minute (1') = 60 seconds (60").
- 1 second (1") = 1/3600 of a degree.
Converting Between Notations
Decimal to Degree-Minute-Second:- Multiply the decimal part by 60 to get minutes.
- Multiply the decimal part of minutes by 60 to get seconds.
- Example: 130.831° = 130° + (0.831 × 60)' = 130° + 49.86' = 130° + 49' + (0.86 × 60)" = 130°49'52".
Degree-Minute-Second to Decimal:
- Convert minutes to degrees by dividing by 60.
- Convert seconds to degrees by dividing by 3600.
- Add all parts.
- Example: 28°45'33" = 28 + (45/60) + (33/3600) ≈ 28.759°.
Using Calculators:
Calculators can convert between decimal degrees and degree-minute-second forms using specific functions.
Radian Measure
This section introduces radians as an alternative unit for measuring angles, particularly useful in advanced mathematics.Definition of a Radian:
- A radian is the measure of a central angle that subtends an arc equal in length to the circle’s radius.
- Formula: θ = s/r (where θ is the angle in radians, s is the arc length, and r is the radius; s and r must be in the same units).
Calculating Radians:
- Example: For an arc length s = 2 cm and radius r = 5 cm, θ = 2/5 = 0.4 rad.
Concentric Circles:
- Circles with the same center but different radii. The ratio of arc length to radius (θ = s/r) remains constant for a given central angle across concentric circles.
Converting Between Degrees and Radians
This section explains how to convert angles between degrees and radians. Key Relationships:
Key Relationships:
A full revolution is 360° or 2π radians: 2π rad = 360°.
1 rad = 180°/π ≈ 57.296°.
1° = π/180 rad.
Conversion Formulas:
- Radians to Degrees: Multiply radians by 180°/π.
Example: 2π/3 rad = (2π/3) × (180°/π) = 120°. - Degrees to Radians: Multiply degrees by π/180°.
Example: 20° = 20 × (π/180°) = π/9 rad.
Common Conversions:
- 30° = π/6 rad
- 45° = π/4 rad
- 60° = π/3 rad
- 90° = π/2 rad
- 180° = π rad
- 360° = 2π rad
Points to Remember
- The circumference of a circle is C = 2πr or C = πd, where π ≈ 3.14 is a constant ratio of circumference to diameter.
- A diameter is twice the radius (d = 2r), and a radius connects the center to the circumference.
- An arc is a portion of the circumference, and a sector is a pie-shaped area formed by two radii and an arc.
- A central angle has its vertex at the circle’s center, measured counterclockwise from the positive horizontal axis in standard position.
- One revolution = 360° = 2π radians. One degree = 1/360 of a revolution, and one radian ≈ 57.296°.
- Convert degrees to minutes and seconds: 1° = 60', 1' = 60". Decimal degrees can be converted to degree-minute-second form and vice versa.
- A radian is the angle subtending an arc equal to the radius: θ = s/r.
- Convert radians to degrees by multiplying by 180°/π; convert degrees to radians by multiplying by π/180°.
- Concentric circles share the same center, and the radian measure of a central angle is consistent across them.
Difficult Words
- Circumference: The total length around a circle’s edge.
- Diameter: A line through the center connecting two opposite points on the circumference.
- Radius: A line from the center to a point on the circumference.
- Arc: A segment of the circumference.
- Sector: A region bounded by two radii and an arc.
- Central Angle: An angle with its vertex at the circle’s center.
- Pi (π): The constant ratio of a circle’s circumference to its diameter, approximately 3.14.
- Radian: A unit of angle measure where the arc length equals the radius.
- Concentric Circles: Circles with the same center but different radii.
Summary
This section consolidates the chapter’s key concepts.Circle Properties:
- Circumference: C = 2πr or C = πd.
- Diameter: d = 2r.
- Arc: Part of the circumference.
- Sector: Area enclosed by two radii and an arc.
- Central Angle: Vertex at the circle’s center.
Angle Measurements:
- Degrees: 360° in a revolution, 1° = 1/360 of a revolution.
- Minutes and Seconds: 1° = 60', 1' = 60", 1" = 1/3600°.
- Radians: θ = s/r, where 2π rad = 360°.
Conversions:
- Radians to degrees: Multiply by 180°/π.
- Degrees to radians: Multiply by π/180°.
Applications:
Calculate circumferences, arc lengths, and angles in practical scenarios like gears, pulleys, and wheels.
|
1 videos|57 docs|4 tests
|
FAQs on Circles, Angles, and Angular Movement Chapter Notes - Mathematics for Grade 10
| 1. What are the main parts of a circle? |  |
| 2. What is Pi (π) and why is it important in circle measurement? |  |
| 3. How do you measure angles in degrees? |  |
| 4. What is the relationship between degrees and radians? |  |
| 5. What are some key points to remember about converting between degrees and radians? |  |














