TITA Based Questions: Time and Work | Quantitative Aptitude (Quant) - CAT PDF Download

Recent trends in the CAT exam show a noticeable rise in TITA (Type In The Answer) questions. This document focuses specifically on TITA-based problems from the topic of Time and Work to aid your preparation.
Q1: The amount of job that Amir, Sunil and Kashish can individually do in a day, are in harmonic progression. Kashish takes twice as much time as Amir to do the same amount of job. If Amir and Sunil work for 4 days and 9 days, respectively, Kashish needs to work for 16 days to finish the remaining job. Then the number of days Sunil will take to finish the job working alone, is
 View Answer
View Answer 
Ans: 27
Let Amir = A , Sunil = S and Kashish = K and
let the time taken by A and K to complete a work is x and 2x days respectively.
Work done in a day is the efficiency of a person.
Hence, if efficiencies of A, S and K are in Harmonic Progression, time taken by them to finish a work will be in Arithmetic Progression.
∴ Time taken by S alone is arithmetic mean of time taken by A and K alone.
⇒ Time taken by S alone = (x + 2x)/2 = 1.5x
Using unitary method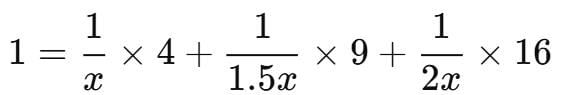 ⇒ x = 4 + 6 + 8
⇒ x = 4 + 6 + 8
⇒ x = 18
∴ S will take 1.5 × 18 = 27 days to finish the job alone.
Q2: Garima and Suhani, working together, can finish a job in 20 days. If Garima does only 60% of her usual work on a day, Suhani must do 150% of her usual work on that day to exactly make up for it. Then, the number of days required by the faster worker to complete the job working alone is
 View Answer
View Answer 
Ans: 36
Let work done per day (efficiency) of Garimaand Suhani are 'g' and 's' units.
A shortfall of 40% for Garima is compensated by 50% extra work done by Suhani.
⇒ 0.4 × g = 0.5 × s
⇒ g/s = 5/4
⇒ Let g = 5x and s = 4x
Together they can complete the work in 20 days.
⇒ Total work to be done = 20 × (5x + 4x) = 180x units
The faster among the two is Garima whose efficiency is 5x.
∴ Time required by Garima alone = 180x / 5x = 36 days.
Q3: Working alone, the times taken by Anjali, Tanya and Maya to complete any job are in the ratio 5 : 8 : 10. They accept a job that they can finish in 4 days if they all work together for 8 hours per day. However, Anjali and Tanya work together for the first 6 days, working 6 hours and 40 minutes per day. Then, the number of hours that Maya will take to complete the remaining job working alone is:
 View Answer
View Answer 
Ans: 6
Ratio of time taken by Anjali, Tanya and Maya is 5 : 8 : 10.
⇒ Ratio of efficiencies of Anjali, Tanya and Maya 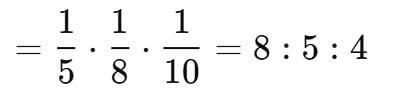
Let their efficiencies be 8x, 5x and 4x respectively per hour.
Total work done by them in 4 days = (8x + 5x + 4x) × 4 × 8 = 17x × 32 = 544x
Now, Anjali and Tanya worked by 6 days working 6 hours 40 minute i.e.
⇒ Time taken by Maya to complete the remaining work =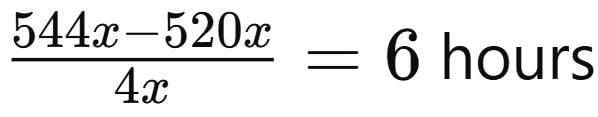
Q4: Bob can finish a job in 40 days, if he works alone. Alex is twice as fast as Bob and thrice as fast as Claire in the same job. Suppose Alex and Bob work together on the first day, Bob and Claire work together on the second day, Claire and Alex work together on the third day, and then, they continue the work by repeating this three-day roster, with Alex and Bob working together on the fourth day, and so on. Then, the total number of days Alex would have worked when the job gets finished, is
 View Answer
View Answer 
Ans: 11
Bob takes 40 days to finish the work.
Alex takes is twice as fast as Bob and hence will take half the time taken by Bob i.e., 20 days.
Alex is also thrice as fast as Claire, hence Claire will take thrice the time taken by Alex, i.e., 60 days.
Time take by
Alex = 20 days
Bob = 40 days
Claire = 60 days
Let the total work to be done = 120 units.
∴ Efficiency of
Alex = 6 units/day
Bob = 3 units/day
Claire = 2 units/day
Work done/cycle = 22 units.
∴ Work done in 5 cycles = 5 × 22 = 110 units
Work left after 5 cycles (15 days) = 120 – 110 = 10 units.
On 16th day Alex and Bob will together complete 9 units of work while remaining 1 unit of work will be completed by Bob and Claire on 17th day.
∴ Alex worked for 10 days in 5 complete cycles + on 16th day i.e., total 11 days.
Q5: Amit, Adil and Aditya are working on a project. Working together Amit and Adil can complete the project in 1 year, Adil and Aditya can complete in 16 months, Aditya and Amit can complete in 2 years. If the person who is neither the fastest nor the slowest works alone, the time in months he will take to complete the project is
 View Answer
View Answer 
Ans: 32
Let the total work to be done = LCM (12, 16, 24) = 48 units.
Let the efficiency of Amit, Adil and Aditya be ‘x’, ‘y’ and ‘z’ units/month⇒ x + y = 48/12 = 4 …(2)
⇒ y + z = 48/16 = 3 …(1)
⇒ z + x = 48/24 = 2 …(3)
Adding all these equations
⇒ x + y + z = 9/2 = 4.5 …(4)
Solving these four equations we get,
x = 1.5, y = 2.5 and z = 0.5
∴ The person who is neither slowest not fastest is Amit with efficiency of 1.5 units/month.
∴ Time required by Amit to complete the task alone
= 48/1.5 = 32 months.
Q6: Anil can paint a house in 12 days while Bhanu can paint it in 16 days. Anil, Bhanu, and Chinmay undertake to paint the house for ₹ 24000 and the three of them together complete the painting in 6 days. If Chinmay is paid in proportion to the work done by him, then the amount in INR received by him is
 View Answer
View Answer 
Ans: 3000
Let the area to be painted = LCM(12, 16) = 48 units.
⇒ Efficiency of Anil = 48/12 = 4 units/day
and Efficiency of Bhanu = 48/16 = 3 units/day
Work done by Anil in 6 days = 6 × 4 = 24 units
Work done by Anil in 6 days = 6 × 3 = 18 units
∴ Remaining work done by Chinmay = 48 – 24 – 18 = 6 units.
⇒ Payment received by Chinmay = 24000/48 × 6 = Rs. 3,000
Alternately,
Fraction of work done by Anil in 6 days = 6/12 = ½
Fraction of work done by Bhanu in 6 days = 6/16 = 3/8
⇒ Fraction of work done by Chinmay in 6 days = 1 - ½ - 3/8 = 1/8
Since, Chinmay completes 1/8th of the work, he will receive 1/8th of the payment.
∴ Chinmay’s payment = 1/8 × 24,000 = Rs. 3,000
Q7: John takes twice as much time as Jack to finish a job. Jack and Jim together take one-thirds of the time to finish the job than John takes working alone. Moreover, in order to finish the job, John takes three days more than that taken by three of them working together. In how many days will Jim finish the job working alone?
 View Answer
View Answer 
Ans: 4
Let John’s efficiency be 1 unit/day.
∴ Jack’s efficiency is 2 units/day.
Jack and Jim’s efficiency is thrice John’s efficienc.
∴ 2 + eJim = 3 × 1
⇒ eJim = 1
John takes three days more than that taken by three of them working together
Let the time taken by all three together is d.
∴ Total work to be done = 4 × d = 1 × (d + 3)
⇒ d = 1
∴ John finished the work in d + 3 = 4 days.
Since, John and Jim have same efficiency, Jim will also finish the work in 4 days.
Q8: A contractor agreed to construct a 6 km road in 200 days. He employed 140 persons for the work. After 60 days, he realized that only 1.5 km road has been completed. How many additional people would he need to employ in order to finish the work exactly on time?
 View Answer
View Answer 
Ans: 40
In 60 days 1.5 kms out of 6 kms is built.
∴ In 60 days 1.5/6 = 1/4th work is done.
To complete the whole work, it would take 4 × 60 = 240 days, i.e., 180 more days.
Days remaining now is 200 – 60 = 140 days.
∴ To complete the remaining work in 140 days, contractor will have to hire more people.
Assuming he hires x more men.
The work which 140 men would take 180 more days, now need to be completed by 140 + x men in 140 days.
∴ 180 × 140 = 140 × (140 + x)
⇒ x = 40
∴ Contractor hires 40 more people.
Q9: Three men and eight machines can finish a job in half the time taken by three machines and eight men to finish the same job. If two machines can finish the job in 13 days, then how many men can finish the job in 13 days?
 View Answer
View Answer 
Ans: 13
Let the work done by one man and one machine per day be x and y respectively.
Three men and eight machines can finish a job in half the time taken by three machines and eight men to finish the same job.
Since efficiency is inversely proportional to the time taken, so the efficiency of 3 men and 8 machines is twice that of 8 men and 3 machines.
∴ (3x + 8y) = 2(8x + 3y)
∴ 13x = 2y.
So, work done by 13 men in a day = work done by 2 machines in a day.
∴ If two machines can finish the job in 13 days, same work will be done by 13 men in 13 days.
Q10: John gets Rs 57 per hour of regular work and Rs 114 per hour of overtime work. He works altogether 172 hours and his income from overtime hours is 15% of his income from regular hours. Then, for how many hours did he work overtime?
 View Answer
View Answer 
Ans: 12
If John works the same number of regular and over-time hours say 'p'
The income would be 57p and 114p
Let's say that he works 'x' hours regular and 'y' hours overtime...
So, the income would be 57x and 114y
we are told that 114y is 15% of 57x
114y = 0.15 × 57x
y = 0.075x
we also know that x + y = 172
therefore, x + 0.075x = 1.075x = 172
x = 160
y = 172 - 160 = 12
Therefore, the number of hours he worked overtime is 12 hours.
Q11: A tank is fitted with pipes, some filling it and the rest draining it. All filling pipes fill at the same rate, and all draining pipes drain at the same rate. The empty tank gets completely filled in 6 hours when 6 filling and 5 draining pipes are on, but this time becomes 60 hours when 5 filling and 6 draining pipes are on. In how many hours will the empty tank get completely filled when one draining and two filling pipes are on?
 View Answer
View Answer 
Ans: 10
Let a filling pipe fills the tank at ‘a’ liters per hour and a draining pipe drains at ‘b’ liters per hour.
Work done by 6 filling and 5 emptying pipes in 6 hours = 6(6a - 5b)
Work done by 5 filling and 6 emptying pipes in 60 hours = 60(5a - 6b)
6(6a – 5b) = 60(5a – 6b)
∴ 6a – 5b = 50a – 60b
∴ 44a = 55b
∴ a = 5b/4
Let the tank gets filled completely in ‘m’ hours when one draining pipe and two filling pipes are on.
Work done by 2 filling and 1 emptying pipes in m hours = m(2a - b)
∴ m(2a – b) = 6(6a – 5b)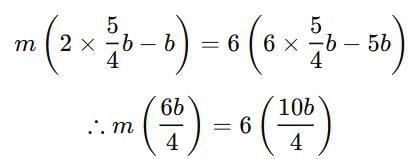 Solving this, we get m = 10
Solving this, we get m = 10
Q12: Ritika would take 15 days working 4 hours per day to complete a certain task whereas Shruti would take 8 days working 5 hours per day to complete the same task. They decide to work together to complete this task. Shruti agrees to work for double the number of hours per day as Ritika, while Ritika agrees to work for double the number of days as Shruti. If Ritika works 2 hours per day, then the number of days Shruti will work, is
 View Answer
View Answer 
Ans: 6
Step 1: Find total work in hours (assuming the task is measured in work hours).
Total work by Ritika = 15 days × 4 hours/day = 60 hours.
Total work by Shruti = 8 days × 5 hours/day = 40 hours.
Since both complete the same task, total work is the same. So, we consider the total work as 60 hours (the higher number).
Step 2: Calculate work rates per hour for Ritika and Shruti.
Ritika's rate = Total work / Total time = 60 hours / (15 days × 4 hours) = 60 / 60 = 1 unit/hour.
Shruti's rate = 60 hours / (8 days × 5 hours) = 60 / 40 = 1.5 units/hour.
Step 3: Define variables for new working hours and days:
Let Ritika work x hours per day.
Ritika works for D days.
Then Shruti works double the number of hours as Ritika = 2x hours/day.
Shruti works half the number of days as Ritika = D/2 days (since Ritika works double the days as Shruti).
Step 4: Given Ritika works 2 hours per day, so x = 2.
Ritika's total work done = (rate) × (hours per day) × (days) = 1 unit/hour × 2 hours/day × D days = 2D units.
Shruti's total work done = 1.5 units/hour × 2x hours/day × (D/2) days
Since x = 2,
Shruti's work = 1.5 × 4 × (D/2) = 3D units.
Step 5: Total work done by both = total work (60 units)
2D + 3D = 60
5D = 60
D = 12 days
Step 6: Find days Shruti works:
Shruti works D/2 = 12/2 = 6 days.
Q13: Three labourers worked together for 30 days, in the course of work, all of them remained absent for few days. One of them was absent for 10 days more than the second labourer and the third labourer did one-third of the total work. How many days more than the third labourer was the first one absent?
 View Answer
View Answer 
Ans: 5
Let k be the part of work labourers can do in one day and x -10, x, y be the number of days for which they remained present. Then
(x − 10) k + xk = 2/3 and yk = 1/3
(2x − 10) 1/3y = 2/3 ⇒ 2x − 10 = 2y ⇒ x − 5 = y
The required number of days= y − (x − 10) = 5
Q14: 12 men and 16 boys can do a piece of work in 5 days and 13 men and 24 boys can do it in 4 days. Compare the daily work done by a man with that done by a boy.
 View Answer
View Answer 
Ans: 2 : 1
12 men + 16 boys can do the work in 5 days.
5 x (12 men + 16 boys) can do the work in 1 day.
Similarly 4 x (13 men + 24 boys) can do the same work in 1 day.
⇒ 52 men + 96 boys = 60 men + 80 boys.
⇒ 8 men = 16 boys or 1 man = 2 boys, i.e. 2 : 1
Q15: If 5 men and 3 boys can reap 23 hectares in 4 days and if 3 men and 2 boys can reap 7 hectares in 2 days, then how many boys must assist 7 men in order that they may reap 45 hectares in 6 days?
 View Answer
View Answer 
Ans: 2
5 men + 3 boys can reap 23 hectares in 4 days.
3 men + 2 boys can reap 7 hectares in 2 days.
14 (5 men + 3 boys) can reap 23 x 14 hectares in 4 days.
23 (3 men + 2 boys) can reap 7 x 2 x 23 hectares in 4 days.
14 (5 men + 3 boys) = 23 (3 men + 2 boys).
1 man = 4 boys. Now 5 men + 3 boys = 23 boys.
23 boys can reap 23 hectares in 4 days.
30 boys can reap 45 hectares in 6 days.
But 30 boys = 28 boys + 2 boys = 7 men + 2 boys.
Hence 2 boys must assist 7 men.
|
167 videos|229 docs|95 tests
|
FAQs on TITA Based Questions: Time and Work - Quantitative Aptitude (Quant) - CAT
| 1. What is the basic formula to calculate work done in time and work problems? |  |
| 2. How do you determine the combined work rate of two or more workers? |  |
| 3. What is meant by 'work' in time and work problems? |  |
| 4. How do you solve problems involving incomplete work? |  |
| 5. Can you explain how to calculate the time taken by a group of workers to complete a job together? |  |





















