TITA Based Questions: Profit and Loss | Quantitative Aptitude (Quant) - CAT PDF Download
As TITA (Type In The Answer) questions gain more weight in the CAT exam, this document focuses on Profit and Loss problems to help you prepare thoroughly and secure valuable marks.
Q1: Jayant bought a certain number of white shirts at the rate of Rs 1000 per piece and a certain number of blue shirts at the rate of Rs 1125 per piece. For each shirt, he then set a fixed market price which was 25% higher than the average cost of all the shirts. He sold all the shirts at a discount of 10% and made a total profit of Rs 51000. If he bought both colors of shirts, then the maximum possible total number of shirts that he could have bought is
View Answer 
Ans: 407
Let the number of white and blue shirts bought is 'w' and 'b' respectively.
Total cost price = 1000w + 1125b
⇒ Average cost price/shirt =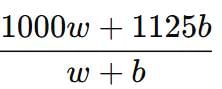
⇒ Average marked price/shirt =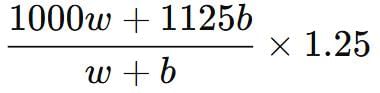
⇒ Average sellingprice/shirt =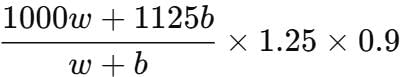
⇒ Total selling price = (1000w + 1125b) × 1.25 × 0.9
∴ Profit = 51000 = (1000w + 1125b) × 1.25 × 0.9 - (1000w + 1125b)
⇒ 51000 = (1000w + 1125b) × (1.25 × 0.9 - 1)
⇒ 51000 = (1000w + 1125b) × (0.125)
⇒ 1000w + 1125b = 408000
⇒ 40w + 45b = 16320
⇒ 8w + 9b = 3264
w + b will be maximum when we maximum the variable with least coefficiency and minimise the variable with highest coefficient.
Least possible value of of b cannot be 0 as at least one shirt of each type is bought.
Hence, the next least possible value of b possible is 8.
∴ b = 8 and w = 399
∴ Highest possible value of w + b = 399 + 8 = 407
Hence, 407.
Q2: Amal buys 110 kg of syrup and 120 kg of juice, syrup being 20% less costly than juice, per kg. He sells 10 kg of syrup at 10% profit and 20 kg of juice at 20% profit. Mixing the remaining juice and syrup, Amal sells the mixture at ₹ 308.32 per kg and makes an overall profit of 64%. Then, Amal’s cost price for syrup, in Rupees per kg, is
View Answer Ans: 160
Let the cost price of juice be Rs. 10x/kg, hence cost price of syrup = 8x/kg
10 kg syrup is sold at 10% profit i.e., at 8.8x/kg.
∴ Total selling price = Rs. 88x
20 kg of juice is sold at 20% profit i.e., at 12x/kg
∴ Total selling price = Rs. 240x
Remaining (110 + 120 – 30 =) 200 kg at Rs. 308.32/kg.
Total cost price of the mixture = 110 × 8x + 120 × 10x = 2080x
⇒ 2080x × 1.64 = 88x + 240x + 308.32 × 200
⇒ 2080x × 1.64 - 328x = 308.32 × 200
⇒ 3083.2x = 308.32 × 200
⇒ x = 20
Cost price of syrup = 8x = 160/kg.
Hence, 160.
Q3: Amal purchases some pens at ₹ 8 each. To sell these, he hires an employee at a fixed wage. He sells 100 of these pens at ₹ 12 each. If the remaining pens are sold at ₹ 11 each, then he makes a net profit of ₹ 300, while he makes a net loss of ₹ 300 if the remaining pens are sold at ₹ 9 each. The wage of the employee, in INR, is
View Answer Ans: 1000
Let the total number of pens Amal bought = x
Also, let the wage of the employee = w
∴ Amal’s total cost price = 8x + w
Total selling price of the first 100 pen = 100 × 12 = 1200
Case 1: The remaining pen when each is sold at Rs. 11
Total selling price of the remaining pen = (x - 100) × 11
⇒ 1200 + 11(x - 100) = 8x + w + 300
⇒ 3x - 200 = w …(1)
Case 2: The remaining pen when each is sold at Rs. 9
Total selling price of the remaining pen = (x - 100) × 9
⇒ 1200 + 9(x - 100) = 8x + w - 300
⇒ x + 600 = w …(2)
Solving (1) and (2) we getx = 400 and w = 1000.
Hence, 1000.
Q4: A person spent Rs. 50000 to purchase a desktop computer and a laptop computer. He sold the desktop at 20% profit and the laptop at 10% loss. If overall he made a 2% profit then the purchase price, in rupees, of the desktop is
View Answer Ans: 20000
Let the price of desktop be Rs. d, and laptop be Rs. (50,000 - d)
Total profit = 2% of 50,000 = Rs. 1,000
⇒ 1000 = 20% of d - 10% of (50000 - d)
⇒ 100000 = 20d - 500000 + 10d
⇒ 30d = 6,00,000
⇒ d = 20,000
Hence, 20000.
Q5: Bina incurs 19% loss when she sells a product at Rs. 4860 to Shyam, who in turn sells this product to Hari. If Bina would have sold this product to Shyam at the purchase price of Hari, she would have obtained 17% profit. Then, the profit, in rupees, made by Shyam is
View Answer Ans: 2160
Let the cost price of the item be C
We are given that Bina sells this at 19% loss or at (1 - 0.19)C = 0.81C at 4860
This gives us the value of C at Rs. 6000
If Bina had sold this at 17% profit, the selling price would have been 1.17 × 6000 = 7020
So Shyam bought the product at 4860 and sold it to Hari at 7020
Giving the profit made by Shyam to be 7020 − 4860 = 2160
Therefore, 2160 is the correct answer.
Q6: A fruit seller has a stock of mangoes, bananas and apples with at least one fruit of each type. At the beginning of a day, the number of mangoes make up 40% of his stock. That day, he sells half of the mangoes, 96 bananas and 40% of the apples. At the end of the day, he ends up selling 50% of the fruits. The smallest possible total number of fruits in the stock at the beginning of the day is
View Answer Ans: 340
Since the mangoes make up 40% of his stock at the beginning of the day, and let the mangoes at the beginning of the day be 4x, So the bananas and apples will be equal to 6x. If the bananas equal y, then the apples would be 6x - y. Totally there are 10x number of fruits.
At the end of the day 50% of mangoes, 96 bananas and 40% of apples are sold and thereby he ends up selling 50% of the fruits.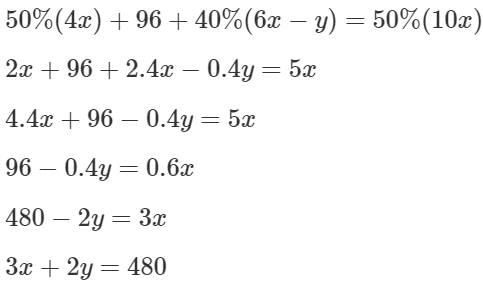
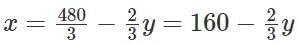(For x to be an integer, y should be a multiple of 3.)
Since y is the number of bananas, y ≥ 96.
Also since the apples are (6x - y) in number...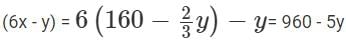
The number of apples must be non-zero.
960 - 5y = 0 when y = 192.
∴ 96 ≤ y < 192 (Also, y needs to be a multiple of 3.)
So, the maximum value that y can take is 189.
For the total number of fruits to be minimum, 10x should be minimum, which happens when x is minimum.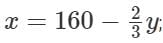
x is minimum when y is maximum.
So the minimum value of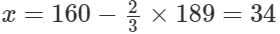 
So, the minimum number of total fruits = 10x = 340.
Q7: Anil invests Rs. 22000 for 6 years in a certain scheme with 4% interest per annum, compounded half-yearly. Sunil invests in the same scheme for 5 years, and then reinvests the entire amount received at the end of 5 years for one year at 10% simple interest. If the amounts received by both at the end of 6 years are same, then the initial investment made by Sunil, in rupees, is
View Answer Ans: 20808
“Anil invests Rs. 22000 for 6 years in a certain scheme with 4% interest per annum, compounded half-yearly.”
Total Amount of Anil’s investment after 6 years =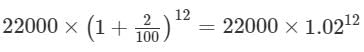
Let Sunil Invest a Principal of P.
“Sunil invests in the same scheme for 5 years, and then reinvests the entire amount received at the end of 5 years for one year at 10% simple interest.”
Total Amount of Sunil’s investment after 6 years =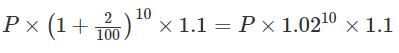
“…the amounts received by both at the end of 6 years are same…”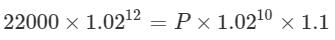
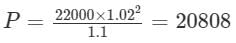
Therefore, Sunil’s investment is Rs. 20808
Q8: Mr. Pinto invests one-fifth of his capital at 6%, one-third at 10% and the remaining at 1%, each rate being simple interest per annum. Then, the minimum number of years required for the cumulative interest income from these investments to equal or exceed his initial capital is
View Answer Ans: 20
Let the capital invested by Mr.Pinto be Rs. 300.
Rs.300 because we deal with one-third, further in the question.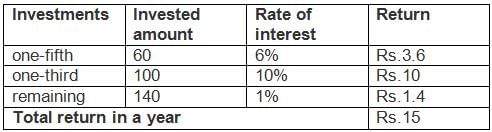
The interest generated is Rs.15 per year.
Let’s say the capital is invested for n years.
When return equals capital…
15 n = 300
n = 20.
Q9: A box has 450 balls, each either white or black, there being as many metallic white balls as metallic black balls. If 40% of the white balls and 50% of the black balls are metallic, then the number of non-metallic balls in the box is
View Answer Ans: 250
The box contains 450 balls
Let’s consider the number of white and black balls to be ‘x’ and ‘y’ respectively.
The number of white metallic balls is the same as black metallic balls.
40% of the white balls and 50% of the black balls are metallic.
So, 0.4x =0.5y
x : y = 5 : 4.
Hence the number of White balls is 250 (100 - metallic and 150 - Non-metallic)
Hence the number of Black balls is 200 (100 - metallic and 100 - Non-metallic)
The total number of non-metallic balls is 250.
Q10: A person invested a certain amount of money at 10% annual interest, compounded half-yearly. After one and a half years, the interest and principal together became Rs 18522. The amount, in rupees, that the person had invested is
View Answer Ans: 16000
A 10% annual interest is a 5% bi-annual interest.
Hence interst for half an year is 5%.
The Principal, P is invested for 1.5 years or 3 terms of half years.
Therefore, P (1 + 5%)3 = 18522
P(1.05)3 = 18522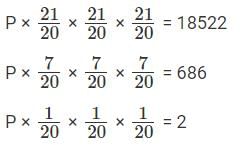
P = 2 × 20 × 20 × 20 = 16000.
Q11: For the same principal amount, the compound interest for two years at 5% per annum exceeds the simple interest for three years at 3% per annum by Rs 1125. Then the principal amount in rupees is
View Answer Ans: 90000
P(1.05)2 – P = CI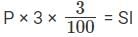
CI = 0.1025 P
SI = 0.09P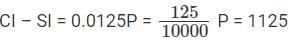
P = 90000
Q12: Veeru invested Rs 10000 at 5% simple annual interest, and exactly after two years, Joy invested Rs 8000 at 10% simple annual interest. How many years after Veeru’s investment, will their balances, i.e., principal plus accumulated interest, be equal?
View Answer Ans: 12
Let assume its equal after N years
Veeru’s investment after N years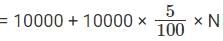 
Joy’s investment after N years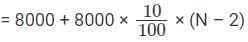 
Equating both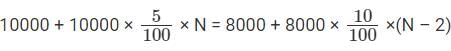
10000 + 500N = 8000 + 800N – 1600
3600 = 300N
N = 12
Q13: In an examination, the score of A was 10% less than that of B, the score of B was 25% more than that of C, and the score of C was 20% less than that of D. If A scored 72, then the score of D was [TITA]
View Answer Ans: 80
From the data,
A scored 72
A's score was 10% less than B
So, Score of B = 80
We know that B was 25% more than C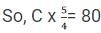
C = 64
Now, we know that D scored 20% less than D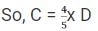
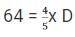
D = 80 marks
Q14: Amal invests Rs 12000 at 8% interest, compounded annually, and Rs 10000 at 6% interest, compounded semi-annually, both investments being for one year. Bimal invests his money at 7.5% simple interest for one year. If Amal and Bimal get the same amount of interest, then the amount, in Rupees, invested by Bimal is [TITA]
View Answer Ans: 20920
The amount on the first investment of Anmol = 12,000 × (1.08) = 12,960
So the Interest on this investment is 12,960 - 12,000 = 960.
The amount on the second investment of Anmol = 10,000 × (1.03)2 = 10,609
So the Interest on this investment is 10,609 - 10,000 = 609.
So the total interest on these returns = 960 + 609 = 1,569.
Bimal has to get this as Simple Interst by investing X rupees at 7.5%
That means, X × 0.075 = 1,569
X = 20,920
So, Bimal has to invest 20,920 rupees.
Q15: In a class, 60% of the students are girls and the rest are boys. There are 30 more girls than boys. If 68% of the students, including 30 boys,pass an examination, the percentage of the girls who do not pass is [TITA]
View Answer Ans: 20
Given that there are 60 % girls and 40 % boys
It is also given that there are 30 more girls than boys.
So, (60 % - 40 %) of total class strength = 30 students
⇒ 20 % of total class strength = 30 students
⇒ Total class strength = 30 x 5 = 150 students
It is also given that 68% of students pass the the examination, which includes 30 boys
So, Number of students passed = 68% of Total students
⇒ Number of students passed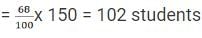 
⇒ Since the number of boys passed is 30,
⇒ Number of girls passed = 102 - 30 = 72
Total number of girls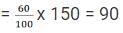 
Total number of girls = Girls who passed + Girls who did not pass
Girls who did not pass = 90 - 72 = 18
Percentage of girls who did not pass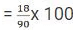 
= 20%
|
166 videos|229 docs|95 tests
|
FAQs on TITA Based Questions: Profit and Loss - Quantitative Aptitude (Quant) - CAT
| 1. What is the basic formula for calculating profit or loss? |  |
| 2. How do you calculate the percentage of profit or loss? | |
| 3. What is the difference between gross profit and net profit? | |
| 4. How can discounts affect profit and loss calculations? | |
| 5. What are some common mistakes to avoid when calculating profit and loss? | |
Extra Questions
,TITA Based Questions: Profit and Loss | Quantitative Aptitude (Quant) - CAT
,Important questions
,study material
,TITA Based Questions: Profit and Loss | Quantitative Aptitude (Quant) - CAT
,ppt
,Exam
,mock tests for examination
,Objective type Questions
,Summary
,practice quizzes
,Semester Notes
,Previous Year Questions with Solutions
,Free
,Viva Questions
,Sample Paper
,MCQs
,TITA Based Questions: Profit and Loss | Quantitative Aptitude (Quant) - CAT
,past year papers
,video lectures
,shortcuts and tricks
;
TITA Based Questions: Profit and Loss Free PDF Download
Importance of TITA Based Questions: Profit and Loss
TITA Based Questions: Profit and Loss Notes
TITA Based Questions: Profit and Loss CAT
Study TITA Based Questions: Profit and Loss on the App
|
© EduRev
|
Education Revolution
|
|
