TITA Based Questions: Percentages | Quantitative Aptitude (Quant) - CAT PDF Download
As TITA (Type In The Answer) questions gain more weight in the CAT exam, this document focuses on Percentages problems to help you prepare thoroughly and secure valuable marks.
Q1: A fruit seller has a stock of mangoes, bananas and apples with at least one fruit of each type. At the beginning of a day, the number of mangoes make up 40% of his stock. That day, he sells half of the mangoes, 96 bananas and 40% of the apples. At the end of the day, he ends up selling 50% of the fruits. The smallest possible total number of fruits in the stock at the beginning of the day is
View Answer 
Ans: 340
Given:
Initial stock consists of mangoes (M), bananas (B), and apples (A)
Mangoes = 40% of total stock ⇒ M = 0.4T
Fruits sold:
Half of mangoes = 0.5M
96 bananas
40% of apples = 0.4A
Total sold = 50% of initial stock = 0.5T
Let:
Total initial fruits (T) = 5x (to make 40% calculation clean)
⇒ M = 2x
Let A = 5a (to make 40% of apples integer)
⇒ B = 5x - 2x - 5a = 3x - 5a
Fruits sold:
1. Mangoes: 0.5 × 2x = x
2. Bananas: 96
3. Apples: 0.4 × 5a = 2a
Total sold = x + 96 + 2a = 0.5 × 5x = 2.5x
Equation:
x + 96 + 2a = 2.5x
⇒ 1.5x = 96 + 2a
⇒ x = 64 + (4a)/3
Find minimum integer solution:
For x to be integer, (4a)/3 must be integer ⇒ a must be multiple of 3
Minimum a = 3:
x = 64 + 4 = 68
Total T = 5x = 340
Q2: In a class, 60% of the students are girls and the rest are boys. There are 30 more girls than boys. If 68% of the students, including 30 boys, pass an examination, the percentage of the girls who do not pass is
View Answer Ans: 20
Let the total number of students be 100x.
So, number of girls and boys are 60x and 40x respectively.
There are 30 more girls than boys ∴ 60x = 40x + 30.
∴ x = 3/2.
Number of students who passed = 68x = 68 × (3/2) = 102 out of which 30 boys passed.
So, number of girls who passed = 102 − 30 = 72
Number of girls who did not pass = 60x − 72
= 60(3/2)− 72
= 90 - 72
= 18.
Required percentage = [18/90] × 100 = 20%.
Hence, 20.
Q3: In an examination, the score of A was 10% less than that of B, the score of B was 25% more than that of C, and the score of C was 20% less than that of D. If A scored 72, then the score of D was
View Answer Ans: 80
Given: A scored 72
A's score was 10% less than B
So, Score of B = 72/0.9 = 80
We know that B was 25% more than C
C x 125 / 100 = 80
On solving
So, C × 5/4 = 80
⇒ C = 64
Now, we know that C scored 20% less than D.
C = 80/100 x D
Upon solving, we get
So, C = 4/5 × D
⇒ 64 = 4/5 × D
⇒ D = 80 marks
Hence, 80.
Q4: Arun's present age in years is 40% of Barun's. In another few years, Arun's age will be half of Barun's. By what percentage will Barun's age increase during this period?
View Answer Ans: 20
Let Barun’s age be 10x.
Arun’s age is 4x.
The difference of these ages in 6x, a constant.
When Arun’s age is 50% of Barun’s age, this difference also would be 50% i.e.,
Barun’s age, at that stage would be 12x.
⇒ Required % = (12x - 10x)/10x × 100% = 20%
It would be increase by 20%.
Alternately,
Let Barun’s age be 10x. Arun’s age is 4x.
In t years, Arun's age will be 50% or half of Barun's age
⇒ (4x + t) = 1/2 × (10x + t)
⇒ t = 2x
∴ Barun's age will become 12x.
⇒ Required % = (12x - 10x)/10x × 100% = 20%
Hence, 20.
Q5: Ravi invests 50% of his monthly savings in fixed deposits. Thirty percent of the rest of his savings is invested in stocks and the rest goes into Ravi's savings bank account. If the total amount deposited by him in the bank (for savings account and fixed deposits) is Rs 59,500, then Ravi's total monthly savings (in Rs) is:
View Answer Ans: 70000
Let the total monthly savings be S.
Investment in FD = 50% of S = 0.5S
Remaining savings = S - 0.5S = 0.5S
Investment in stocks = 30% of 0.5S = 0.15S
Total invested amount (FD + stocks) = 0.5S + 0.15S = 0.65S
Remaing amount that is invested in savings account = 0.35S.
⇒ 0.35S + 0.5S = 59,500
⇒ 0.85S = 59500.
⇒ S = 70,000.
Hence, 70,000.
Q6: A box has 450 balls, each either white or black, there being as many metallic white balls as metallic black balls. If 40% of the white balls and 50% of the black balls are metallic, then the number of non-metallic balls in the box is
View Answer Ans: 250
Let the number of white balls be x and black balls be y
So we get x + y = 450 (1)
Now metallic black balls = 0.5y
Metallic white balls = 0.4x
From condition 0.4x = 0.5y
we get 4x - 5y = 0 (2)
Solving (1) and (2) we get
x = 250 and y = 200
Now number of Non Metallic balls
= 0.6x + 0.5y
= 150 + 100
= 250
Q7: The strength of an indigo solution in percentage is equal to the amount of indigo in grams per 100 cc of water. Two 800 cc bottles are filled with indigo solutions of strengths 33% and 17%, respectively. A part of the solution from the first bottle is thrown away and replaced by an equal volume of the solution from the second bottle. If the strength of the indigo solution in the first bottle has now changed to 21% then the volume, in cc, of the solution left in the second bottle is
View Answer Ans: 200
We have two bottles (A and B), each initially containing 800 cc of indigo solution:
Bottle A: 33% strength → 264 g indigo
Bottle B: 17% strength → 136 g indigo
Process:
1. Remove x cc from Bottle A and discard it.
Removes 0.33x g indigo from A
Leaves (800 – x) cc and (264 – 0.33x) g in A
2. Add x cc from Bottle B to Bottle A.
Adds 0.17x g indigo to A
New indigo in A: 264 – 0.33x + 0.17x = 264 – 0.16x g
Final volume in A returns to 800 cc
3. New strength in A is 21%:
(264 – 0.16x) / 800 = 0.21
⇒ 264 – 0.16x = 168
⇒ x = 600 cc
Result:
Volume taken from Bottle B = 600 cc
Solution left in Bottle B = 800 – 600 = 200 cc
Q8: John gets Rs 57 per hour of regular work and Rs 114 per hour of overtime work. He works altogether 172 hours and his income from overtime hours is 15% of his income from regular hours. Then, for how many hours did he work overtime?
View Answer Ans: 12
It is given that John works altogether 172 hours i.e including regular and overtime hours.
Let a be the regular hours, 172-a will be the overtime hours
John's income from regular hours = 57 × a
John's income for working overtime hours = (172-a) × 114
It is given that his income from overtime hours is 15% of his income from regular hours
a × 57 × 0.15 = (172-a) × 114
a = 160
The number of hours for which he worked overtime = 172 - 160 = 12 hrs
Q9: In an election, there were four candidates and 80% of the registered voters casted their votes. One of the candidates received 30% of the casted votes while the other three candidates received the remaining casted votes in the proportion 1 : 2 : 3. If the winner of the election received 2512 votes more than the candidate with the second highest votes, then the number of registered voters was:
View Answer Ans: 62800
Let the total number of registered voters be 100x.
Number of votes casted = 80x
Votes for Candidate 1 = 30% of 80x = 24x
∴ Remaining three candidates will recieve = 80x - 24x = 56x votes.
Remaining 3 candidates get votes in the ratio of 1 : 2 : 3 of the remaining 56x votes.
Highest number of votes is received by Candidate 4 while second highest is by Candidate 1.
⇒ 28x – 24x = 2512
⇒ x = 2512/4 = 628
∴ total number of registered votes = 100x = 62800
Q10: Identical chocolate pieces are sold in boxes of two sizes, small and large. The large box is sold for twice the price of the small box. If the selling price per gram of chocolate in the large box is 12% less than that in the small box, then the percentage by which the weight of chocolate in the large box exceeds that in the small box is nearest to
View Answer Ans: 127
Let the weight and price of small box is ‘w’ and ‘p’ respectively.
∴ Selling price per gram for small box = p/w
Now, selling price per gram for large box = 0.88p/w
Also, selling price for the whole box = 2p.
⇒ Weight of the large box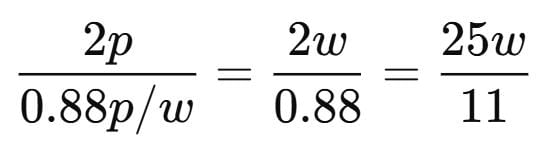 
∴ Required percentage=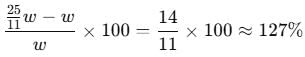 
Q11: Raj invested ₹ 10000 in a fund. At the end of first year, he incurred a loss but his balance was more than ₹ 5000. This balance, when invested for another year, grew and the percentage of growth in the second year was five times the percentage of loss in the first year. If the gain of Raj from the initial investment over the two year period is 35%, then the percentage of loss in the first year is
View Answer Ans: 10
Let the loss incurred by Raj in first year = P%
∴ Amount remaining after 1st year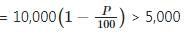 
…(1)
Now the percentage growth next year = 5P%
∴ Amount after 2 years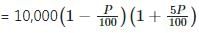 
Overall growth after 2 years is 35%, hence amount after 2 years should be 10,000 × 1.35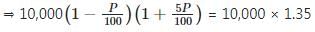
⇒ 10000 – 5P2 + 400P = 13500
⇒ 5P2 - 400P + 3500 = 0
⇒ P2 – 80P + 700 = 0
⇒ P = 10% or 70%.
P cannot be 70% since amount remaining after 1st year has to be greater than 5000 [from (1)]
∴ P = 10%
Q12: In a tournament, a team has played 40 matches so far and won 30% of them. If they win 60% of the remaining matches, their overall win percentage will be 50%. Suppose they win 90% of the remaining matches, then the total number of matches won by the team in the tournament will be
View Answer Ans: 84
Matches so far:
Total played = 40
Won = 30% of 40 = 12
Let the number of remaining matches be ‘n’.
The team wins 60% i.e., 0.6n matches.
There overall win percentage is 50% i.e., half
⇒ 12 + 0.6n = ½ (40 + n)
⇒ 24 + 1.2n = 40 + n
⇒ n = 80
Now, if the team wins 90% of these 80 remaining matches, they will win 90% of 80 = 72 more matches.
∴ Total matches won = 12 + 72 = 84
Q13: In May, John bought the same amount of rice and the same amount of wheat as he had bought in April, but spent ₹ 150 more due to price increase of rice and wheat by 20% and 12%, respectively. If John had spent ₹ 450 on rice in April, then how much did he spend on wheat in May?
View Answer Ans: 560
John spent Rs. 450 on rice in April hence he will spend 450 × 1.2 = 540 on rice in May.
He spends Rs. 90 extra on rice.
He also spends a total of Rs. 150 more in May compared to April
⇒ He spends 150 – 90 = Rs. 60 more on wheat in May compared to April.
∴ His expenditure on wheat in April on wheat = 60/0.12 = Rs. 500.
⇒ His expenditure on wheat in May = 500 + 60 = Rs. 560.
Q14: Meena scores 40% in an examination and after review, even though her score is increased by 50%, she fails by 35 marks. If her post-review score is increased by 20%, she will have 7 marks more than the passing score. The percentage score needed for passing the examination is
View Answer Ans: 70
Let the total marks be 100x.Meena's score = 40x.
Meena's score after review = 40x + [(40x)/2] = 60x.
Passing marks = 60x + 35.
Post review score × (6/5) = 7 + Passing marks
∴ 60x × (6/5) = 60x + 42.
Solving this equation we get; x = 3.5.
So, passing marks = 60x + 35 = (60 × 3.5) + 35 = 245 and total marks = 100x = 100 × 3.5 = 350.
Percentage score needed to pass the examination = (Passing marks/Total marks) × 100 = (245/350) × 100 = 70%.
Q15: On selling a pen at 5% loss and a book at 15% gain, Karim gains Rs. 7. If he sells the pen at 5% gain and the book at 10% gain, he gains Rs. 13. What is the cost price of the book in Rupees?
View Answer Ans: 80
Let the cost price of one pen and one book be 100p and 100b respectively.
On selling a pen at 5% loss and a book at 15% gain, Karim gains Rs. 7.
∴ 95p + 115b = 7 + (100p + 100b) ⇒ 15b − 5p = 7 ...(1)
On selling the pen at 5% gain and the book at 10% gain, he gains Rs. 13.
∴ 105p + 110b = 13 + (100p + 100b)
⇒ 10b + 5p = 13 ...(2)
Solving (1) and (2), we get; b = 4/5.
So, cost price of one book = 100b = 100 × (4/5) = Rs. 80.
|
166 videos|229 docs|95 tests
|
FAQs on TITA Based Questions: Percentages - Quantitative Aptitude (Quant) - CAT
| 1. What are the basic concepts of percentages that I should know for the exam? |  |
| 2. How can I effectively solve percentage problems in a limited time during the exam? | |
| 3. Are there any common mistakes to avoid when dealing with percentages? | |
| 4. What types of percentage questions are typically asked in exams? | |
| 5. Can you provide tips for mastering percentage calculations? | |
shortcuts and tricks
,Objective type Questions
,practice quizzes
,Free
,Previous Year Questions with Solutions
,mock tests for examination
,past year papers
,Semester Notes
,Important questions
,TITA Based Questions: Percentages | Quantitative Aptitude (Quant) - CAT
,MCQs
,Sample Paper
,study material
,Viva Questions
,Extra Questions
,Summary
,video lectures
,ppt
,TITA Based Questions: Percentages | Quantitative Aptitude (Quant) - CAT
,TITA Based Questions: Percentages | Quantitative Aptitude (Quant) - CAT
,Exam
,
TITA Based Questions: Percentages Free PDF Download
Importance of TITA Based Questions: Percentages
TITA Based Questions: Percentages Notes
TITA Based Questions: Percentages CAT
Study TITA Based Questions: Percentages on the App
|
© EduRev
|
Education Revolution
|
|
within 7 days!