TITA Based Questions: Ratio & Proportion | Quantitative Aptitude (Quant) - CAT PDF Download

As TITA (Type In The Answer) questions gain more weight in the CAT exam, this document focuses on Ratio and Proportion problems to help you prepare thoroughly and secure valuable marks.
Q1: The number of coins collected per week by two coin-collectors A and B are in the ratio 3 : 4. If the total number of coins collected by A in 5 weeks is a multiple of 7, and the total number of coins collected by B in 3 weeks is a multiple of 24, then the minimum possible number of coins collected by A in one week is
 View Answer
View Answer 
Ans: 42
Let the number of coins collected by A and B in one week be 3x and 4x respectfully.
The total number of coins collected by A in 5 weeks = 15x
For 15x to be a multiple of 7, x has to be a multiple of 7.
The total number of coins collected by B in 3 weeks = 12x
For 12x to be a multiple of 24, x has to be a multiple of 2.
Therefore, x has to be a multiple of 7 × 2 = 14
The minimum value that x can take is 14.
So, the minimum coins collected by A in one week = 3x = 3 × 14 = 42.
Q2: A container has 40 liters of milk. Then, 4 liters are removed from the container and replaced with 4 liters of water. This process of replacing 4 liters of the liquid in the container with an equal volume of water is continued repeatedly. The smallest number of times of doing this process, after which the volume of milk in the container becomes less than that of water, is
 View Answer
View Answer 
Ans: 7
Every time 10% of the mixture is replace with a pure adulterant (here water), the concentration of the mixture becomes 90% of the initial concentration.
Similarly when a proportion p of a mixture is replaced with pure adulterant, the concentration of the mixture becomes (1 - p) times the previous concentration. (0 ≤ p ≤ 1)
Here p = 4/40 = 0.1
Initially there was pure milk, so the strength of the mixture is 100% or 1 (in terms of proportion)
After repeating the process n times the concentration of Milk in the mixture will be 1 × 0.9n
For the volume of milk to be less than the volume of water, p should be less than 0.5
So we are looking for the smallest n, such that 1 × 0.9n < 0.5
This happens when n = 7
Q3: In an examination, the average marks of students in sections A and B are 32 and 60, respectively. The number of students in section A is 10 less than that in section B. If the average marks of all the students across both the sections combined is an integer, then the difference between the maximum and minimum possible number of students in section A is
 View Answer
View Answer 
Ans: 63
Let the possible average marks of all the students combined be a.
We know that 32 < a < 60.
If the overall average is ‘a’, the ratio of the number of students in class A to the number of students in class B is (60 - a) : (a - 32).
Also when there are equal numbers of students in class A and class B, the value of a is simply 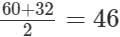 .
.
If there are more students in class B than class A, the value of a is greater than 46 and if there are fewer students in class B than class A, the value of a is less than 46.
Since there are 10 more students in class B than class A, 46 < a < 60.
The extreme values of the number of students depend on the extreme values of a.
When a = 47, the ratio of students in class A to class B is 13 : 15
15x - 13x = 10
2x = 10
x = 5
Total number of students in class A = 13x = 65.
When a = 56, the ratio of students in class A to class B is 1 : 6
6x - x = 10
5x = 10
x = 2
Total number of students in class A = x = 2.
The difference between the maximum and minimum possible number of students in section A is 65 - 2 = 63
Q4: The average of all 3-digit terms in the arithmetic progression 38, 55, 72, ..., is
 View Answer
View Answer 
Ans: 548
The common difference of the AP, 38, 55, 72, … is 17.
The smallest 3-digit number in the AP is 106 and the largest 3-digit number in it is 990
We need to find the value of,
106 + 123 + … + 973 +990
= 106 + (106 + 17) + (106 + 2 *17) + …. + (106 + 52 *17)
= 53(106) + 17(1 + 2 + 3 + … + 52)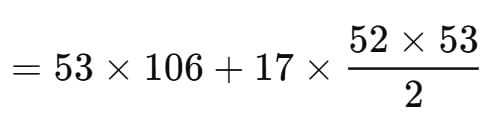
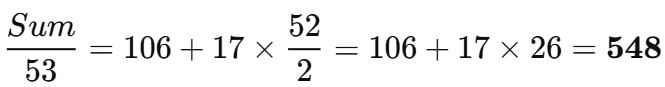
Q5: Pinky is standing in a queue at a ticket counter. Suppose the ratio of the number of persons standing ahead of Pinky to the number of persons standing behind her in the queue is 3 : 5. If the total number of persons in the queue is less than 300, then the maximum possible number of persons standing ahead of Pinky is
 View Answer
View Answer 
Ans: 111
The ratio of the number of persons standing ahead of Pinky to the number of persons standing behind her in the queue is 3 : 5.Let’s assume that there are 3x number of people ahead of Pinky, then the number of people behind her will be 5x.
The total number of people in the queue is 8x + 1.
Since the total number of people in the queue is less than 300.
8x + 1 < 300
x ≤ 37
To find the maximum number of people ahead of Pinky, we take the maximum possible value of x, which is 37.
Therefore, the maximum number of people ahead of Pinky is 3 x 37 = 111
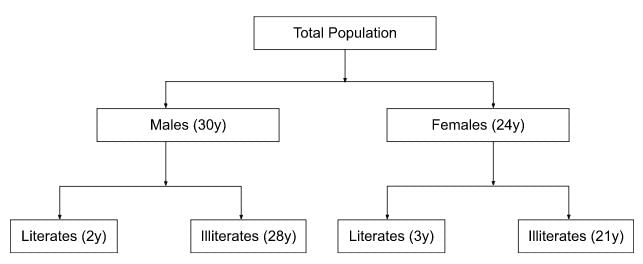
Q6: In a village, the ratio of number of males to females is 5 : 4. The ratio of number of literate males to literate females is 2 : 3. The ratio of the number of illiterate males to illiterate females is 4 : 3. If 3600 males in the village are literate, then the total number of females in the village is
 View Answer
View Answer 
The ratio of the number of males to females is 5 : 4
The ratio of the number of literate males to literate females is 2 : 3.
The ratio of the number of illiterate males to illiterate females is 4 : 3.
Let,
The number of males to females is 5x, 4x
The number of literate males to literate females is 2y, 3y.
The number of illiterate males to illiterate females is 4z, 3z.
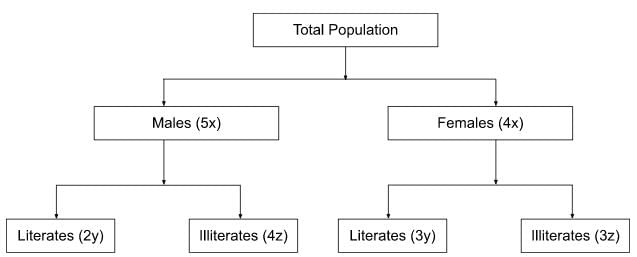 We know that the ratio of the number of males to females is 5 : 4
We know that the ratio of the number of males to females is 5 : 4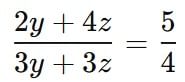 4(2y + 4z) = 5(3y + 3z)
4(2y + 4z) = 5(3y + 3z)8y + 16z = 15y + 15z
z = 7y
 3600 males in the village are literate.
3600 males in the village are literate.2y = 3600
y = 1800
Total number of females = 24y = 24(1800) = 43,200
Q7: The arithmetic mean of scores of 25 students in an examination is 50. Five of these students top the examination with the same score. If the scores of the other students are distinct integers with the lowest being 30, then the maximum possible score of the toppers is
 View Answer
View Answer 
Ans: 92
The arithmetic mean of the scores of 25 students = 50
Sum of scores of these students = 25 × 50 = 1250
For the scores of the top 5 students to be as high as possible, the score of the bottom 20 students should be as low as possible.
The minimum score is 30, and the scores of the bottom 20 students are distinct integers.
In order for the bottom 20 scores to be as low as possible, they must be,
30, 31, 32, … 49
Sum of the bottom 20 scores
= 30 + 31 + 32 + … + 49
= (30 + 0) + (30 + 1) + (30 + 2) + … + (30 + 19)
= 20 × 30 + (0 + 1 + 2 + 3 + … + 19)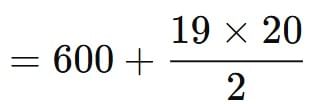
= 600 + 190
= 790
Therefore, the maximum sum of the scores of the top 5 students = 1250 - 790 = 460
The maximum score of the five toppers, since they all scored the same marks = 490/5 = 92
Q8: A tea shop offers tea in cups of three different sizes. The product of the prices, in INR, of three different sizes is equal to 800. The prices of the smallest size and the medium size are in the ratio 2 : 5. If the shop owner decides to increase the prices of the smallest and the medium ones by INR 6 keeping the price of the largest size unchanged, the product then changes to 3200. The sum of the original prices of three different sizes, in INR, is
 View Answer
View Answer 
Ans: 34
Since the prices of the small and medium cups are in the ratio 2 : 5,
Let us assume the prices of the small, medium and large cups to be 2x, 5x and y.
We are given that the product of the three prices is 800.
Therefore, (2x)(5x)(y) = 800 —- (1)
If the price of the smallest and the medium cups are increased by 6, then the product becomes 3200
(2x + 6) (5x + 6) (y) = 3200 —- (2)
Dividing (2) by (1)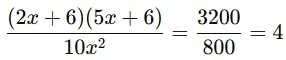
(2x + 6) (5x + 6) = 40 x2
10 x2 + 42x + 36 = 40 x2
30 x2 - 42x - 36 = 0
10 x2 - 14x - 12 = 0
10 x2 - 20x + 6x - 12 = 0
10 x(x - 2) + 6(x - 2) = 0
(10x + 6) (x - 2) = 0
x = 2 or x = -0.6
x can’t be negative and hence x = 2
WKT, (2x)(5x)(y) = 800
(4)(10)(y) = 800
y = 20
Therefore, the sum of the prices = 2x + 5x + y
= 2(2) + 5(2) + 20
= 4 + 10 + 20
= 34
Q9: From a container filled with milk, 9 litres of milk are drawn and replaced with water. Next, from the same container, 9 litres are drawn and again replaced with water. If the volumes of milk and water in the container are now in the ratio of 16 : 9, then the capacity of the container, in litres, is
 View Answer
View Answer 
Ans: 45
Let’s assume the capacity of the container is ‘c’
Let’s track down the milk which is retained.
The milk retained after taking first 9 litres from the container is 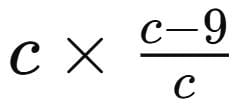
The milk retained after taking next 9 litres from the container is 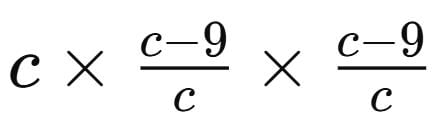
The volumes of milk and water in the container are now in the ratio of 16 : 9.
The milk in the container is 16/25
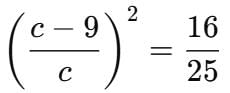
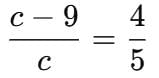 c = 45
c = 45
Q10: In a football tournament, a player has played a certain number of matches and 10 more matches are to be played. If he scores a total of one goal over the next 10 matches, his overall average will be 0.15 goals per match. On the other hand, if he scores a total of two goals over the next 10 matches, his overall average will be 0.2 goals per match. The number of matches he has played is
 View Answer
View Answer 
Ans: 10
Let the number of matches already played be x, then over the next ten matches if one more goal is scored, the average goals become 0.15. Further if the player scores two goals the average becomes 0.2.
From this we can see that one extra goal is increasing the average by 0.05 (0.2 - 0.15).
Hence it can be said that the total number of matches played till the end is 20.
Therefore, x + 10 = 20
Hence, x = 10
Q11: The strength of an indigo solution in percentage is equal to the amount of indigo in grams per 100 cc of water. Two 800 cc bottles are filled with indigo solutions of strengths 33% and 17%, respectively. A part of the solution from the first bottle is thrown away and replaced by an equal volume of the solution from the second bottle. If the strength of the indigo solution in the first bottle has now changed to 21% then the volume, in cc, of the solution left in the second bottle is
 View Answer
View Answer 
Ans: 200
Given that, there are two 800cc bottles of indigo solution with strengths of 33% and 17% respectively.
Some amount of the solution from bottle 1 is replaced by the same amount of solution from bottle 2.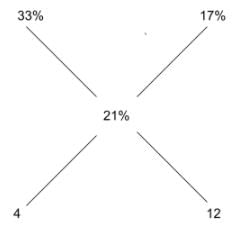 In 800cc of a new solution of strength 21% has two solutions in the ratio 1:3.
In 800cc of a new solution of strength 21% has two solutions in the ratio 1:3.
200cc of 33% solution and 600cc of 17% solution combined to give 21% solution of indigo
Hence, the remaining solution in the bottle 2 is 200cc.
Q12: Suppose hospital A admitted 21 less Covid infected patients than hospital B, and all eventually recovered. The sum of recovery days for patients in hospitals A and B were 200 and 152, respectively. If the average recovery days for patients admitted in hospital A was 3 more than the average in hospital B then the number admitted in hospital A was
 View Answer
View Answer 
Ans: 35
Let's consider the number of patients admitted in hospital A and hospital B to be 'x' and ‘x + 21'
Given that, the sum of recovery days for patients in hospitals A and B were 200 and 152, respectively.
The average recovery days for patients admitted in hospital A was 3 more than the average in-hospital B.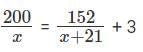
By solving the above equation we get x = 35.
Hence, the number of patients admitted to hospital A is 35.
Q13: Rick is thrice as old as Tom and Harry is twice as old as Rick. If Rick's age is 1 year less than the average age of all three, then Harry's age, in years, is
 View Answer
View Answer 
Ans: 18
Let's consider Tom's age to be 'x' years.
Rick is thrice as old as Tom,
Rick's age = 3 × x = 3x
Harry is twice as old as Rick,
Harry's age = 2 × 3x = 6x
Rick's age is 1 year less than the average age of all three,
3x = Average(x, 3x, 6x) - 1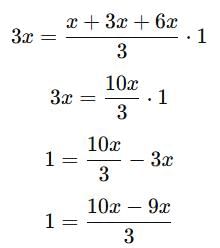 1 = x/3
1 = x/3
x = 3
Harry's age = 6x = 6 × 3 = 18 years.
Q14: A sum of money is split among Amal, Sunil and Mita so that the ratio of the shares of Amal and Sunil is 3:2, while the ratio of the shares of Sunil and Mita is 4:5. If the difference between the largest and the smallest of these three shares is Rs 400, then Sunil’s share, in rupees, is
 View Answer
View Answer 
Ans: 800
A : S : M
3 : 2
4 : 5
6 : 4 : 5
Given difference 6k – 4k = 2k = 400
k = 800
Q15: Ashok purchased pens and pencils in the ratio 2: 3 during his first visit and paid Rs. 86 to the shopkeeper. During his second visit, he purchased pens and pencils in the ratio 4: 1 and paid Rs. I 12 . The cost of a pen as well as a pencil in rupees is a positive integer. If Ashok purchased four pens during his second visit, then the amount he paid in rupees for the pens during the second visit is __________.
 View Answer
View Answer 
Ans: 100
Ratio of pen : pencil is 2:3 and he spends Rs 86
Next time The ratio of pen and pencil is 4:1 and he spends Rs 112
Second time Ashok purchased 4 pens, So the ratio of Pen and Pencil is 4:1
Hence he purchased 4 pens and 1 pencil during his second visit
Let price of pen be 'x' and price of pencil be 'y'
Then,
4x + y = 112. -----(2)
2x + 3y = 86 -----(1)----(From first visit)
(1) Is in Ratios, so it can be 4x + 6y = 86 (or)
6x + 9y = 86 (or)
8x + 12y = 86
Since, From (2), 4 pen and a pencil costs Rs 112
4 pens and 6 pencils has too cost more than 112 (Given that Cost of a pen and pencil is a positive integer)
In that case 4x + 6y = 86 (or)
6x + 9y = 86 (or)
8x + 12y = 86
These possibilities are ruled out
Only possibility is 2x + 3y = 86
Solving (1) and (2) by Elimination Method
We get y = 12 ---> Cost of a pen
On second visit, he pays a total of Rs 112, One pencil and 4 pen.
1 Pencil costs Rs 12, 112 - 12 = Rs 100
He paid Rs 100 during his second visit for the pens.
The answer is 100
|
167 videos|238 docs|95 tests
|
FAQs on TITA Based Questions: Ratio & Proportion - Quantitative Aptitude (Quant) - CAT
| 1. What is the basic definition of ratio and proportion? |  |
| 2. How do you simplify a ratio? |  |
| 3. What are some real-life applications of ratios and proportions? |  |
| 4. What is the difference between direct and inverse proportion? |  |
| 5. How can you solve problems involving ratios and proportions effectively? |  |





















