TITA Based Questions: Linear and Quadratic Equations | Quantitative Aptitude (Quant) - CAT PDF Download

As TITA (Type In The Answer) questions gain more weight in the CAT exam, this document focuses on Linear and Quadratic Equations problems to help you prepare thoroughly and secure valuable marks.
Q1: The number of integral solutions of equation 2|x|(x2 + 1) = 5x2 is?
 View Answer
View Answer 
Ans: 3
Case 1: x ≥ 0 ⇒ |x| = x
∴ 2 × x × (x2 + 1) = 5x2
⇒ 2x(x2 + 1) = 5x2
⇒ 2x(x2 + 1) - 5x2 = 0
⇒ x[2(x2 + 1) - 5x] = 0
⇒ x(2x2 – 5x + 2) = 0
⇒ x(2x2 – 4x - x + 2) = 0
⇒ x[2x(x – 2) - (x - 2)] = 0
⇒ x(2x - 1)(x - 2) = 0
⇒ x = 0 or ½ or 2.
We need only integral solutions hence acceptable answers are 0 and 2.
Case 2: x < 0 ⇒ |x| = -x
∴ 2 × -x × (x2 + 1) = 5x2
⇒ -2x(x2 + 1) = 5x2
⇒ 2x(x2 + 1) + 5x2 = 0
⇒ x[2(x2 + 1) + 5x] = 0
⇒ x(2x2 + 5x + 2) = 0
⇒ x(2x2 + 4x + x + 2) = 0
⇒ x[(2x(x + 2) + (x + 2)] = 0
⇒ x(2x + 1)(x + 2) = 0
⇒ x = 0 or -1/2 or -2
We need only integral solutions hence acceptable answers are 0 and -2.
∴ Acceptable integral solutions are -2, 0 and 2, i.e., 3 integral solutions.
Hence, 3.
Q2: Let α and β be two distinct root of the equation 2x2 – 6x + k = 0, such that (α + β) and αβ are the two roots of the equation x2 + px + p = 0. Then the value of 8(k - p)?
 View Answer
View Answer 
Ans: 6
α and β be two distinct root of 2x2 – 6x + k = 0,
∴ α + β = -(-6)/2 = 3
And, α × β = k/2 = k/2
Now, 3 and k are the roots of the equation x2 + px + p = 0.
∴ Sum of the roots = 3 + k/2 = -(p)/1 = -p …(1)
∴ Product of the roots = 3 × k/2 = (p)/1 = p …(2)
(1) + (2)
⇒ 3 + k/2 + 3k/2 = p – p = 0
⇒ k = -3/2
⇒ p = -9/4 [from (2)]
Now, we need to find 8(k - p)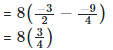
= 6
Hence, 6.
Q3: The equation x3 + (2r + 1)x2 + (4r - 1)x + 2 = 0 has -2 as one of the roots. If the other roots are real, then the minimum possible non-negative integer value of r is?
 View Answer
View Answer 
Ans: 2
Let p and q be the other two real roots of the given cubic equation.
Product of the three roots of the given cubic equation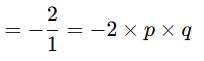
⇒ q = 1/p
∴ The three roots are -2, p and 1/p
Sum of the three roots of the given cubic equation 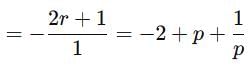
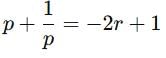
We know than sum of a number and its reciprocal is either less than or equal to - 2 or greater than or equal to 2.
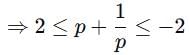
⇒ 2 ≤ -2r + 1 ≤ -2
⇒ 1 ≤ -2r ≤ -3
⇒ -1/2 ≥ r ≥ 3/2
∴ Least non-negative integral value of r is 2.
Hence, 2.
Q4: Let k be the largest integer such that the equation (x - 1)2 + 2kx + 11 = 0 has no real roots. If y is a positive real number, then the least possible value of k/4y + 9y is?
 View Answer
View Answer 
Ans: 6
The given equation can be written as: x2 - 2x + 1 + 2kx + 11 = 0
⇒ x2 + (2k - 2)x + 12 = 0
The given quadratic has no real roots, hence discriminant is less than 0.
⇒ (2k - 2)2 - 4 × 1 × 12 < 0
⇒ 4(k - 1)2 - 48 < 0
⇒ (k - 1)2 < 12
Largets integral value of k satisying above inequality is 4.
Now, we have k/4y + 9y
= 4/4y + 9y
= 1/y + 9y
We know AM ≥ GM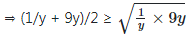
⇒ (1/y + 9y)/2 ≥ 3
⇒ 1/y + 9y ≥ 6
∴ Least possible value of 1/y + 9y = 6.
Hence, 6.
Q5: A quadratic equation x2 + bx + c = 0 has two real roots. If the difference between the reciprocals of the roots is 1/3, and the sum of the reciprocals of the squares of the roots is 5/9, then the largest possible value of (b + c) is
 View Answer
View Answer 
Ans: 9
Let the roots of the given quandratic equation be p and q.
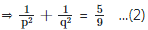
Squaring (1) we get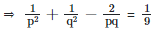
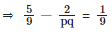
⇒ pq = 9/2 = c
From (2) we get
⇒ 9(p2 + q2) = 5p2q2
⇒ 9(p2 + q2) = 5(pq)2
⇒ 9((p + q)2 - 2pq) = 5(9/2)2
⇒ (p + q)2 - 9 = 45/4
⇒ (p + q)2 = 81/4
⇒ (p + q) = ± 9/2 = - b
largest possible value of b = 9/2
∴ Largest possible value of a + b = 9/2 + 9/2 = 9.
Hence, 9.
Q6: The number of integral solutions of the equation 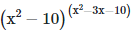 = 1 is
= 1 is
 View Answer
View Answer 
Ans: 4
Given, 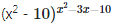
For this to be equal to 1
Case 1: x2 - 10 = 1 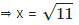
Rejected as x is not an integer.
Case 2: x2 – 3x – 10 = 0
⇒ (x – 5)(x + 2) = 0
⇒ x = 5 or -2 i.e., 2 integral values of x.
Case 3: x2 – 10 = -1 and x2 – 3x – 10 = even
If x2 – 10 = -1 ⇒ x = ±3
For both x = +3 and -3 x2 – 3x – 10 is even, hence, 2 integral values of x.
⇒ Total 4 integral values of x are possible.
Hence, 4.
Q7: A tea shop offers tea in cups of three different sizes. The product of the prices, in INR, of three different sizes is equal to 800. The prices of the smallest size and the medium size are in the ratio 2 : 5. If the shop owner decides to increase the prices of the smallest and the medium ones by INR 6 keeping the price of the largest size unchanged, the product then changes to 3200. The sum of the original prices of three different sizes, in INR, is
 View Answer
View Answer 
Ans: 34
Let the price of small, medium and large cups be Rs. 2x, 5x and p respectively.
⇒ 2x × 5x × p = 800 …(1)
Also, (2x + 6) × (5x + 6) × p = 3200 …(2)
(2) = (1) × 4
⇒ (2x + 6) × (5x + 6) × p = 2x × 5x × p × 4
⇒ 10x2 + 42x + 36 = 40x2
⇒ 30x2 - 42x - 36 = 0
⇒ 5x2 – 7x – 6 = 0
⇒ 5x2 – 10x + 3x – 6 = 0
⇒ (5x + 3)(x - 2) = 0
⇒ x = 2
∴ Price of small cup = 2x = 4
Price of medium cup = 5x = 10
Price of large cup = 800/(4 × 10) = 20
⇒ Sum of the prices of three cups = 4 + 10 + 20 = 34.
Hence, 34.
Q8: The number of distinct real roots of the equation 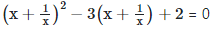 equals
equals
 View Answer
View Answer 
Ans: 1
Let x + 1/x = y
⇒ y2 – 3y + 2 = 0
⇒ (y – 1)(y – 2) = 0
⇒ y = 1 or 2
We know, sum of a number and its reciprocal are either ≤ 2 or ≥ 2.
∴ y = 2⇒ x + 1/x = 2
This is only possible when x = 1 hence, only one real root.
Hence, 1.
Q9: One year payment to the servant is Rs. 90 plus one turban. The servant leaves after 9 months and receives Rs. 65 and turban. Then find the price of the turban
 View Answer
View Answer 
Ans: 10
Payment for 12 months = 90 + t {Assuming t as the value of a turban}
Payment for 9 months should be ¾(90 + t)
Payment for 9 months is given to us as 65 + t
Equating the two values we get
¾(90 + t) = 65 + t
270 + 3t = 260 + 4t
t = 10 Rs.
Q10: The cost of 3 hamburgers, 5 milk shakes, and 1 order of fries at a certain fast food restaurant is $23.50. At the same restaurant, the cost of 5 hamburgers, 9 milk shakes, and 1 order of fries is $39.50. What is the cost of 2 hamburgers, 2 milk shakes, and 2 orders of fries at this restaurant?
 View Answer
View Answer 
Ans: 15
3H + 5M + 1F = 23.50
5H + 9M + 1F = 39.50
2H + 2M + 2F = ?
Calculate 2(Equation 1) – (Equation 2)
H + M + F = 2×23.5 – 39.5
H + M + F = 7.5
2H + 2M + 2F = 15.
Q11: How many integer solutions are there for the equation: |x| + |y| =7?
 View Answer
View Answer 
Ans: 28
x can take any integer value from [-7,7].
So, there are 15 valid values of x.
For each of these values, there are 2 corresponding values of y. eg: For x = 3; y can be 4 or -4.
Except when x = 7 or -7; where the only possible value of y is 0.
Total valid values of x = 13×2 + 1 + 1 = 28.
Q12: Given that three roots of f(x) = x4 + ax2 + bx + c are 2, -3, and 5, what is the value of a + b + c?
 View Answer
View Answer 
Ans: 79
We have to find out a + b + c
f(1) is 1 + a + b + c
So, we need to find out f(1) – 1
Let the 4th root be r
Coefficient of x3 is - (Sum of the roots)
0 = - (r + 2 -3 + 5)
r = - 4
So, f(x) = (x – 2) (x + 3) (x + 4)(x – 5)
f(1) = (-1)×4×5×(-4) = 80
a + b + c = f(1) – 1 = 79.
Q13: If x =2+22/3 +21/3, then the value of x3 -6x2 + 6x is:
 View Answer
View Answer 
Ans: 2
x =2+22/3+21/3
x – 2 = 22/3+21/3
(x – 2)3 = (22/3+21/3)3
x3 – 6x2 + 12x – 8 = 22 + 3. 24/3.21/3 + 3. 22/3.22/3 + 2
x3 – 6x2 + 12x – 8 = 4 + 3.25/3 + 3.24/3 + 2
x3 – 6x2 + 12x – 8 = 6 + 6.22/3 + 6.21/3 = (12 + 6.22/3 + 6.21/3) – 6
x3 – 6x2 + 12x – 8 = 6x – 6
x3 – 6x2 + 6x = 2.
Q14: Find the value of 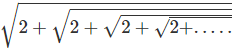
 View Answer
View Answer 
Ans: 2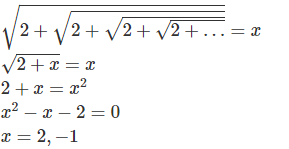
as the value of the expression will be positive, we can reject x=-1.
Hence, x=2.
Q15: If α , β and γ are the roots of the equation x3 − 7x + 3 = 0 what is the value of α4 + β4 + γ4 ?
 View Answer
View Answer 
Ans: 98
Writing the equation as
(x − α)(x − β)(x − γ) = 0, expanding and equating coefficients we get :
αβγ = −3
αβ + αγ + βγ = −7
α + β + γ = 0
From
α2+ β2 +γ2 = (α + β + γ)2−2(αβ + αγ + βγ) = 14
α2β2 + α2γ2 + α2β2 = (αβ + αγ + βγ)2− 2 (α2βγ + αβ2γ + αβγ2)
= (αβ + αγ + βγ)2 − 2αβγ(α + β + γ)
=49
Then α4 + β4 + γ4 = (α2 + β2 + γ2)2 − 2 (α2β2 + α2γ2 + α2β2)
=142−2.49 = 98
|
174 videos|243 docs|95 tests
|
FAQs on TITA Based Questions: Linear and Quadratic Equations - Quantitative Aptitude (Quant) - CAT
| 1. What are linear equations and how do they differ from quadratic equations? |  |
| 2. How can I solve a linear equation? |  |
| 3. What methods can be used to solve quadratic equations? |  |
| 4. What is the significance of the discriminant in a quadratic equation? |  |
| 5. how can i check if my solution to a linear or quadratic equation is correct? |  |
| 5.="" how="" can="" i="" check="" if="" my="" solution="" to="" a="" linear="" or="" quadratic="" equation="" is="" correct?="" |  |
| 5. how can i check if my solution to a linear or quadratic equation is correct? |  |





















