Grade 9 Exam > Grade 9 Notes > AP Statistics > Chapter Notes: Representing a Categorical Variable with Tables
Representing a Categorical Variable with Tables Chapter Notes | AP Statistics - Grade 9 PDF Download
Introduction to Organizing Data
Raw data can be overwhelming and difficult to interpret without proper organization. Statistics provides tools to structure and analyze data effectively. The process often begins with organizing data into tables, followed by creating visual representations like graphs to uncover patterns and insights. For categorical variables, tables are a foundational step, but graphical displays like bar graphs and pie charts offer a more intuitive way to visualize trends and distributions.
Frequency Tables
Imagine conducting a survey in an AP Statistics class to assess how stressful students find their academic workload, with response options of "very stressful," "somewhat stressful," or "not stressful." After collecting 30 responses, how do we make sense of the data?
A frequency table is an effective way to summarize this data. It lists each category and counts the number of responses in each one. For example, a frequency table for qualitative data, such as stress levels, displays categories in one column and their corresponding counts in another. Tallies (e.g., ||||) can help count responses during data collection.
In this case, the variable "stress level" is an ordinal variable because the categories have a natural order (very > somewhat > not stressful), though the differences between categories aren't precisely measurable. The table below illustrates a hypothetical frequency table for the survey:
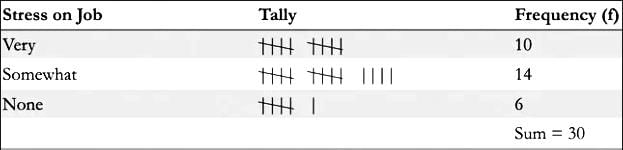 The sum of frequencies always equals the total number of responses, in this case, 30.
The sum of frequencies always equals the total number of responses, in this case, 30.Relative Frequency Tables
To gain deeper insights, we can extend frequency tables by calculating relative frequencies and percentages. A relative frequency is computed by dividing the frequency of a category by the total number of responses. The percentage is then found by multiplying the relative frequency by 100.
- Relative Frequency = Frequency of a category / Total frequency
- Percentage = Relative Frequency × 100
A relative frequency table replaces counts with proportions or percentages. For example, using the stress survey data, if 10 students reported "very stressful," the relative frequency is 10/30 = 0.333, or 33.3%. The table might look like this:
From this, we can conclude that 33.3% of students find their workload very stressful, and combining "very" and "somewhat" stressful categories, 80% (33.3% + 46.7%) report at least some stress. The sum of relative frequencies should equal 1.00, and percentages should total 100%, though rounding may cause slight variations.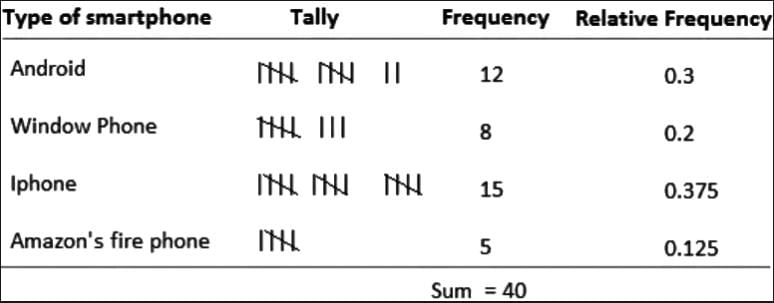
Example: Frequency and Relative Frequency Tables
Consider a dataset: 2, 3, 3, 5, 5, 5, 7, 7, 9. A frequency table counts how often each value appears:
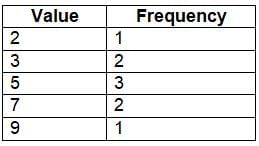 A relative frequency table expresses these counts as proportions:
A relative frequency table expresses these counts as proportions: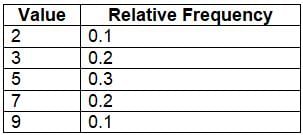 These tables help identify patterns, such as the value 5 being the most frequent, and are essential for summarizing data.
These tables help identify patterns, such as the value 5 being the most frequent, and are essential for summarizing data.Question for Chapter Notes: Representing a Categorical Variable with TablesTry yourself: What does a frequency table display?View Solution
Key Terms
- Bar Graph: A bar graph uses bars to represent different categories, with each bar’s height or length indicating the frequency or value of that category. It’s an effective way to compare categories and identify trends in categorical data.
- Ordinal Variable: An ordinal variable is a categorical variable with a defined order among its categories, but the differences between categories aren’t measurable. For example, stress levels (very, somewhat, none) can be ranked but not quantified precisely.
- Pie Chart: A pie chart is a circular graph divided into slices, where each slice represents a category’s proportion of the total. It’s useful for visualizing how categories contribute to the whole dataset.
The document Representing a Categorical Variable with Tables Chapter Notes | AP Statistics - Grade 9 is a part of the Grade 9 Course AP Statistics.
All you need of Grade 9 at this link: Grade 9
|
12 videos|106 docs|12 tests
|
FAQs on Representing a Categorical Variable with Tables Chapter Notes - AP Statistics - Grade 9
| 1. What is a frequency table and how is it used in organizing data? |  |
Ans.A frequency table is a tool used to organize data by displaying the number of times each category or value occurs within a dataset. It helps in summarizing the distribution of categorical variables, making it easier to identify patterns and trends in the data.
| 2. How do you create a relative frequency table? |  |
Ans.To create a relative frequency table, first, calculate the frequency of each category in your dataset. Then, divide each frequency by the total number of observations to obtain the relative frequency. Finally, present the results in a table format, showing both the categories and their corresponding relative frequencies, often expressed as a percentage.
| 3. What is the difference between frequency tables and relative frequency tables? |  |
Ans.Frequency tables display the actual count of occurrences for each category in a dataset, while relative frequency tables show the proportion of each category relative to the total number of observations. This means relative frequency can provide a clearer understanding of the data's distribution, particularly when comparing categories of different sizes.
| 4. Why are frequency and relative frequency tables important in statistics? |  |
Ans.Frequency and relative frequency tables are important because they provide a clear and concise way to summarize and analyze categorical data. They help researchers and analysts identify trends, make comparisons, and draw conclusions about the data, facilitating better decision-making based on the findings.
| 5. Can frequency tables be used for both categorical and numerical data? |  |
Ans.Frequency tables are primarily designed for categorical data, but they can also be adapted for numerical data by grouping the data into categories or intervals. In such cases, the table will show the number of observations that fall within each interval, allowing for the analysis of the distribution of numerical data in a similar manner to categorical data.
Related Searches















